前言
何为强连通分量?
在一个有向图中,若这个图的子图中,任意两点间可以相互到达,那么这个子图就叫做强连通分量。
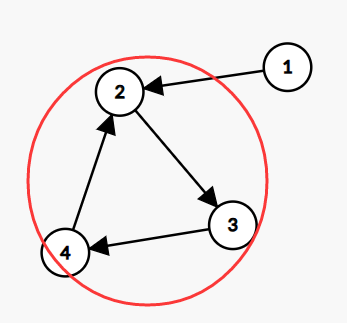
Tarjan 算法求强连通分量
模板题:Luogu P2863 [USACO06JAN] The Cow Prom S
思想
Tarjan算法过程:
以下图为例做演示。
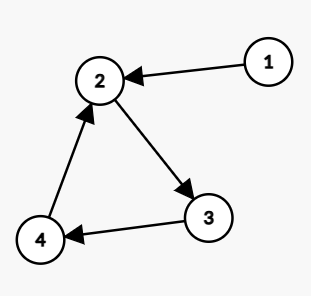
我们定义两个数组 \(dfn\) 和 \(low\)。
含义:
\(dfn_i\):表示节点 \(i\) 在 DFS 搜索时,被访问的时间点(时间戳)。
\(low_i\):表示节点 \(i\) 通过有向边可以回溯到的最早时间点。
我们再创建一个栈 \(s\),用于存放已经被访问过的节点,用 \(vis_i\) 表示 \(i\) 节点当前在不在栈内。
DFS 原则,先访问,后操作。
我们从一号节点开始,现将 \(1\) 号节点访问,放入栈内。
q.push(1),vis_1=1,dfn_1=low_1=1。
s:(栈顶)1(栈底)。
根据 DFS 访问顺序,再将 \(2\) 号节点访问。
q.push(2),vis_2=1,dfn_2=low_2=2。
s:(栈顶)2 1(栈底)。
访问 \(3\) 号节点。
q.push(3),vis_3=1,dfn_3=low_3=3。
s:(栈顶)3 2 1(栈底)。
访问 \(4\) 号节点。
q.push(4),vis_4=1,dfn_4=low_4=4。
s:(栈顶)4 3 2 1(栈底)。
此时整个图已经访问完毕了,然后从栈顶开始更新 \(low\) 数组。
先看 \(4\),\(4\) 号节点可以通过一条有向边到 \(2\) 号节点。
发现 \(2\) 号节点的时间戳 \(dfn_2=2<dfn_4=4\),那么此时更新 low_4=low_2=2。
再看 \(3\),\(3\) 号节点可以通过两条有向边(\(3\) -> \(4\) -> \(2\))到 \(2\) 号节点。
发现 \(2\) 号节点的时间戳 \(dfn_2=2<dfn_3=3\),那么此时更新 low_3=low_2=2。
然后来看 \(2\),\(2\) 号节点无法通过有向边回溯到更早的时间点,那么我们可以说 \(2\) 号节点是一个强连通分量的起始位置,从栈顶到 \(2\) 号节点都属于一个强连通分量,此时我们判断到 \(low_2=dfn_2\),那么我们进行出栈,一直出到 \(2\) 位置,那么所出的所有节点都属于一个强连通分量,即 {2,3,4}。
同样地,\(1\) 号节点也是一个单独的强连通分量 {1}。
重复操作,直至所有点都被更新完毕。
Code
定义 \(fa_i\) 表示 \(i\) 节点所在的强连通分量中的父亲(可以理解为一个强连通分量的代表点),\(sum_i\) 表示 \(i\) 所代表的强连通分量内有多少个点。
Code:
#include <bits/stdc++.h>
#define ll long long
const int N = 1e4 + 5,M = 5e4 + 5;
using namespace std;
inline int read(){
int r = 0,w = 1;
char c = getchar();
while (c < '0' || c > '9'){
if (c == '-'){
w = -1;
}
c = getchar();
}
while (c >= '0' && c <= '9'){
r = (r << 3) + (r << 1) + (c ^ 48);
c = getchar();
}
return r * w;
}
int n,m;
struct edge{
int nxt,to;
}e[M];
int head[N],cnt = 0;;
void edge_add(int x,int y){
cnt++;
e[cnt].nxt = head[x];
head[x] = cnt;
e[cnt].to = y;
}
namespace tj{
int tot = 0,dfn[N],low[N],fa[N],sum[N];
bool vis[N];
stack<int> s;
void tarjan(int x){
tot++;
dfn[x] = low[x] = tot;
vis[x] = 1;
s.push(x);
for (int i = head[x];i;i = e[i].nxt){
int v = e[i].to;
if (!dfn[v]){
tarjan(v);
low[x] = min(low[x],low[v]);
}
else if (vis[v]){
low[x] = min(low[x],dfn[v]);
}
}
if (low[x] == dfn[x]){
int pre;
do {
pre = s.top();
s.pop();
fa[pre] = x;
vis[pre] = 0;
sum[x]++;
}while (pre != x);
}
}
}
using namespace tj;
int main(){
n = read(),m = read();
for (int i = 1;i <= m;i++){
int x = read(),y = read();
edge_add(x,y);
}
for (int i = 1;i <= n;i++){
if (!dfn[i]){
tarjan(i);
}
}
int ans = 0;
for (int i = 1;i <= n;i++){
if (fa[i] == i && sum[i] > 1){
ans++;
}
}
printf("%d",ans);
return 0;
}