经典题。
考虑 dp,然后发现你根本 d 不动。
冷静思考,发现原因在于,无法在较小的复杂度内确定选数的状态。
遇到这种情况可以考虑容斥。设 \(f(i)\) 表示强制选 \(i\) 个位置满足 \(|p_j-j|=k\)。
显然 \(\text{ans}=\sum\limits_{i=0}^n(-1)^if(i)(n-i)!\),因为根据容斥,剩下的位置可以随便填。问题变成了计算 \(f(i)\)。
以行为下标,列为值,画出网格图,发现使得 \(|p_j-j|=k\) 的位置如下图灰色区域:

(这是 \(k=1\) 的情况。)
选一个格子 \((x,y)\) 意味着 \(a_x=y\),显然如果选了一个格子,那么与其同行或同列的格子就由于与其冲突而不能选,我们的目标是选出 \(i\) 个灰色格子。
给冲突的格子画上边:
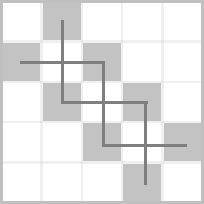
显然这是几条链的形式,\(f(i)\) 即求大小为 \(i\) 的独立集个数。
对每条链分别考虑,我们知道一条点数为 \(n\) 的链上取出 \(m\) 个互不相邻的点的方案数为 \(\dbinom{n-m+1}{m}\)。
然后暴力卷积就做完了。