之前我们讲了基尔霍夫定律,但是只讲了其原理并没有提到其具体的运算,而是采用了欧姆定律的计算方法。这一次我们将正式的学习基尔霍夫定律。
电压降
之前我们提到过负载就像一个石头阻碍电流,现在想象一下假如我们就是电流,负载是个山坡。
我们作为电流在再爬山时需要克服山坡的大小(电阻大小),电压在我们后面推着我们走。假如这个山坡太高,但是电压不够大,就会导致推了一半就没有力气,我们作为电流也就过不去这个山坡。
假如电压足够给力,把我们推到了山顶,但是这时电压已经气喘吁吁没有力气。
当我们下山时,因为此时处于下坡(经过电阻),便不再需要电压去推我们。这个时候电压就会变小,但是我们电流还是会正常流动。
也就是说当电流流过电阻时,电阻的前方和后方会电压下降的情况。
我们之前提到过电压有两个符号,分别是"E"和“V”。
- E就是我们电源电压的符号,通常来说很少用到。
- V也就是伏特是我们经常使用的电压符号,他就代表电压降,每流过一个负载电压都会降低,这也和我们之前讨论的串联电路分配的电压的情况遥相呼应。所谓的分配电压就是这么分配的。
欧姆定律中电压降的计算公式:
一般来说我们平常说的电压都是指电压降,因为E作为电源电压是固定的,大多数时候并没有什么意义,也不需要我们计算。
需要注意的是我们有时候会在图示中表示电压降,如下图
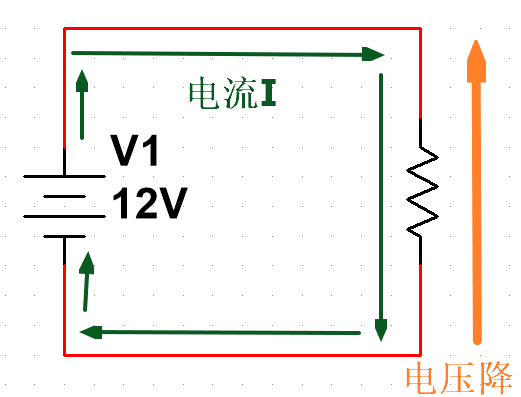
这里电压降的箭头指向上方的意思是
- 箭头所指的方向的电压比箭头尾端的电压更高。
- 因为电流都是从电压高的方向流向电压低的方向。
- 需要注意的是这种箭头只是表示电压降的符号,而非表示电压方向的符号。
- 在之后描述电压降时一般我都会注明,没有注明的箭头就是电压方向。
电流守恒定律
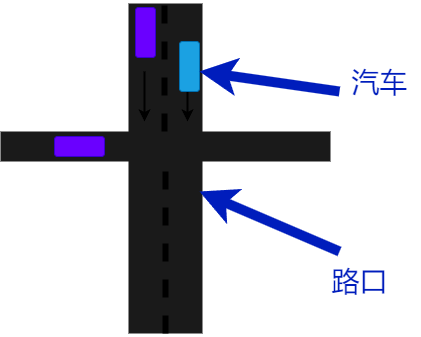
我们想象一个交通路况,有很多车辆从不同的道路进入或是离开这个路口。每条道路的宽度(电阻)不同,所以车辆(电流)通过的速度也不同。
但是无论车辆如何在这个路口穿梭。进入到路口的汽车数量一定是等于离开路口的汽车数量。
这就是电流守恒定律,一般也被称为基尔霍夫第一定律。
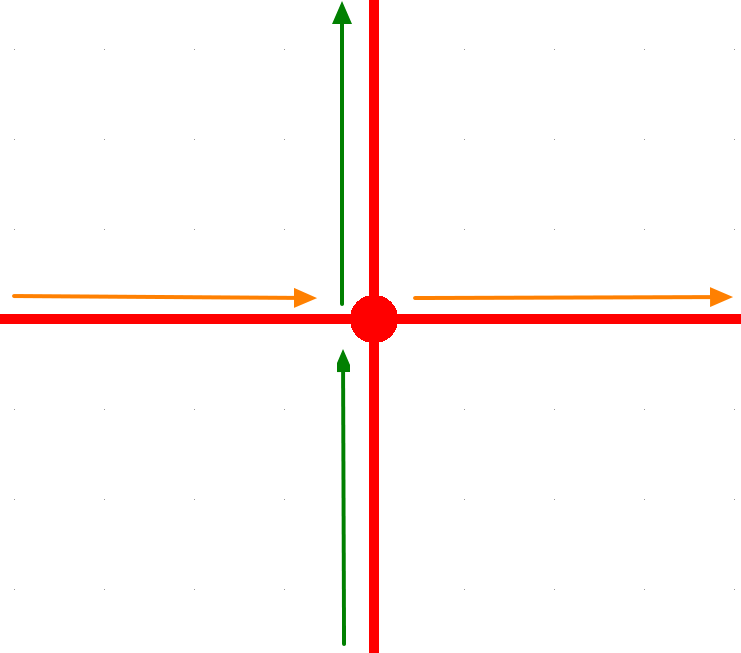
也就是说如果这两根导线相连,其接点的电流的和,就是两根导线的总电流。
电压守恒定律
电压守恒定律也被称为"基尔霍夫第二定律"。
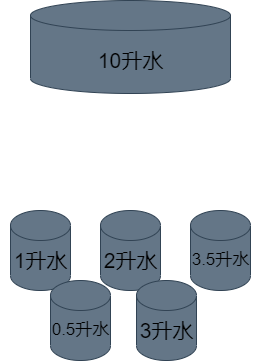
上图中有一个大桶装着5升水。假如这个大桶是电源,里面装着的水是电压,而电阻或是其他元器件负载则是下面的小桶。
当我们将装满水的大桶倒入每一个小桶时,每个小桶都会装满水,直到大桶的水倒完。
也就是说,所有小桶的水加起来就是大桶的水。
这就是电压守恒定律,在一个闭合电路中电源提供的电压等于在电路中被消耗的电压。同样的道理,电路中所有被消耗的电压加在一起就是电源的电压。
电压守恒的数学公式为:
联立方程与矩阵(预备)
例如:
或是
都可以是联立方程,所谓联立方程就是指两个或更多的方程同时成立,其中的未知数需要满足所有方程。这些方程被"联立"在一起,因为我们需要找到一组解使得所有的方程都成立。
比如在上面的第一个例子中我们就需要找到xy既可以满足结果等于7同时也要等于5的解。
联立方程其实我们每个人都接触过,他就是中学时期经常出现的方程组,但是我们这次学习不再是用老办法也就是画图代入消元来解方程因为其效率太低且繁琐,而是采用矩阵和行列式。
为了符合标题“从零学”,我们暂时先把联立方程放在后面,首先来学习基本的方程。
变量
变量:变量就像是一个盒子,我们可以把任何数字放进去。在数学方程中我们通常使用字母
- x
- y
- z
来表示变量。
常数
常数:常数是一个固定的值,他不会改变,1就是1,2就是2。例如在:
1和3就是常量。
系数
系数:系数也是一个常数,他乘以一个变量,例如在
1就是x的系数。
加法
加法就是将两个数字相加,得到的结果被叫做"和"
比如
2与11就是和
减法
减法就是两个数字相减,得到的结果被叫做"差"
比如
0和1就是差
乘法
乘法是指两个数相乘
比如
其中
- 乘号左面的叫做被乘数,也就是"6,1"
- 乘号右面的叫做乘数,也就是"5,3"
- 乘法运算的结果叫做积,也就是"5,12"
乘法是被乘数与乘数个被乘数相加得到的就是积。
- 比如:5*6就是6个5相加,换成加法表达就是"5+5+5+5+5+5=30"
所以本质上乘法就是加法的简写。
除法
除法是指两个数相除
比如
其中
- 乘号左面的叫做被除数,也就是"10,8"
- 乘号右面的叫做除数,也就是"2,4"
- 乘法运算的结果叫做商,也就是"5,2"
除法是看被除数包含着多少个除数。
- 比如:10/2就是看10里面有多少个2,换成减法的表达就是"10-2-2-2-2-2=0"。当结果等于0时说明这个除法算式可以被整除,也就是10可以被2整除。
- 当我们计算"10/3"时,换成减法的表达式就是"10-3-3-3=1",这时当再减3时就会导致结果小于0,我们一般便不会再再减下去。所以10包括3个3,就是是说算式"10/3"的商为"3",这个多余的1我们简称为"余",所以完整的说法就是"10/3"的商为"3余1"
- 当我们计算"10/11"时,减法的表达式就是"10-11=-1",通常来说,如果出现负数就代表这个除法除不开,也就是10不包含11.通常这被认为和"10/0"一样没意义。
除法与乘法不同,乘法只是加法的简写,但是除法不只是减法的简写,它包含着一套独立的逻辑,衍生出了众多新规则。
除法其本质是判断被除数是否包含除数,并且可以得出被除数包含多少个除数。
因数(约数)
如果整数a能被整数b整除,那么就可以说b是a的因数。
- 比如,1、2、3都是3的因数,因为他们都可以将3整除
所谓的整除我们在除法中讲过,就是没有余数。至于整数是什么,自己搜。
因数就是一个数的“分配器”,它可以将这个数平均分配,没有剩余。
倍数
如果一个整数a能被另一个整数b整除,那么a就是b的倍数。
- 比如10是5的倍数,因为10可以被5整除
简单地说它和因数是相反的关系,如果a是b的因数那么b就是a的倍数
- 比如3是6的因数,那么6就是3的倍数
质数(素数)
质数是大于1的数以及它自身。比如5的质数就是5和1。
公倍数
所谓的公倍数就是两个数共同的倍数,比如2和3的公倍数可以是"6,12,18"等等。
因为这些数既可以被2整除也可以被3整除。
还是用苹果举例子,假如你有6个苹果,那么你可以将这6个苹果完整的分给3个或是2个人。但是你如果有7个苹果,就不能将其完整的分给两个人或是3个人,所以7不是2和3的公倍数
公因数(公约数)
公因数就是指能同时整除几个整数的数。
- 比如我们有两个数,分别是12和15,我们可以看到1和三既可以整除12也可以整除15所以1和3是12和15的约数。
你说了这么多,我一个都没记住怎么办?
我自己也记不住
没关系,毕竟我们生活在一个信息化的现代世界。
当你一个都没记住时可以使用科技,不过需要明白的是你也没有必要真的记住每一个东西是什么、它的定义是什么,但是你必须要知道在数学中有这么个东西,当你遇到问题时你才能找到关于它的解决办法。

分数
分数是一个数字,同时他也是一个未完成状态的除法算式。
比如
分数由分子和分母组成,横线上面的是分子,下面的是分母。
分数可以被看成一个除法算式,你可以将其进行除法运算,比如将$$\frac{10}{5}$$看作是"(10/5)",也就是分子除以分母,也只能是分子除以分母。
但是你也可以把它视为一个独立的完整的数字,当把分数看作是一个完整的数字时,其运算规则会复杂一些,但是当你经过完整的应试教育洗刷后就很容易找到他们的技巧和规律,感兴趣自行搜索,我们直接使用计算器。
结合律
结合律适用于加法和乘法,它的含义是当你在做加法或是乘法的运算时,你可以改变数字的分组方式,但是他们的结果不会改变,通常加法结合律的形式如下:
乘法结合律形式如下:
在之后的我们会省略乘号,因为每次书写都很麻烦,而是采用ab,他的意思就是"a*b"(对于常数与常数我们仍然会使用乘号,如"1*2")。
现在让我们来演示一下加法乘法的结合律:
-
对于加法
假如我们有一个加法算式\[1+(2+3) \]我们可以改变其分组的形式写成
\[(1+2)+3 \]他们的结果都是6。
-
对于乘法
假如我们有一个乘法算式\[(1*6)1 \]我们可以改写成
\[1(6*1) \]他们的结果都等于6
交换律
交换律同样适用于加法和乘法,当我们在做加法和乘法的运算时我们可以改变数字的运算顺序,但是结果不会改变。
加法交换律形式
乘法交换律形式
-
假如我们有一个加法算式
\[1+2 \]我们可以改写成
\[2+1 \] -
假如我们有一个乘法算式
\[1*4 \]我们可以改写成
\[4*1 \]
交换律与结合律的扩展
我们拿树上的苹果举例子
-
交换律这种性质是自然存在的,比如树上的苹果,左面有2个右面有5个,无论你是先数左边还是先数右边,苹果的总数都是7个。
-
结合律也一样是自然存在的,比如树左面有2个苹果、右面有5个苹果、上面有5个苹果。无论你先摘右面的还是先摘左面的或是上面的,只要你把苹果摘完。那么不管你从哪里摘最终到你手里的都是12个苹果
等式
等式就是等号两边的数或是式子相等,如
方程
首先,我们需要理解什么是方程。你可以把方程想象成一个秤,等号=就像是秤的中心,它的两边需要保持平衡。比如,我们有一个简单的方程2 + 3 = 5,你可以把它想象成在秤的一边放了2个苹果和3个苹果,另一边放了5个苹果,两边的重量是一样的,所以秤是平衡的。
但是,如果我们有一个未知数,比如2 + x = 5,这就像是在秤的一边放了2个苹果和一些我们不知道数量的橙子,另一边放了5个苹果。我们的任务就是找出需要放多少个橙子才能让秤保持平衡。在这个例子中,我们需要放3个橙子,也就是x = 3。
一元一次方程
在这里所谓的"元",就是指方程中有几个未知数。"次"就是未知数的最高次数。
- 在这里为一次也就是X,如果是2次就是X^2,也就是x*x
通常一元一次方程的形式是
其中a和b是常数,且这个方程可以使用公式来求出:
现在有一个方程:
使用公式得到
我们来验证一下
显然是正确的。
一元二次方程
通常一元二次方程的一般形式是:
其中a,b,c是常数,并且a不等于0。
解一元二次方程的公式为:
其中
叫做根号,用来表示开方运算。比如根号9就是3的二次方,也就是"3^2",因为3*3等于9
被称为判别式,如果这个方程大于0说明这个方程有两个不同的实数解,等于0说明有两个相同的实数解,小于0有两个复数解
现在我们有一个一元二次方程:
使用公式得出
依据判别式得出大于0,有两个实数解,所以我们使用公式:
让我们验证一下
没有问题,因为我们将分数转换为小数所以产生了一些精度误差。
- 虽然在数学领域我们可以直接将分数作为解,但是在电路领域我们需要更直观的数字。比如你问别人电流是多少时别人告诉你电流是"5分之16.5安"就很难受。
- 同时由于在运算过程中将分数转换小数有时要面临保留多少位的取舍,所以如无必要尽量的在运算过程中保持分数的形式,在结束时将分数转换为小数,一般来说是保留小数点后三位比较保险。
- 关于复数解,一般我们得到的复数解需要将它变成复平面得到其坐标,然后将其放置到相量中使用或是直接用复数与其他东西计算。
- 对于在方程中得到的复数,一般形式为:
-
我们也需要把这种形式的分数转换为正常的复数才能用复平面
-
示例:
\[x^2+4=0 \]\[b^2-4ac=0^2-4*1*4=-16 \]\[x=\frac{-0+\sqrt{-16}}{2*1}=\frac{-0+4i}{2}=0+2i \]\[x=\frac{-0-\sqrt{-16}}{2*1}=\frac{-0+4i}{2}=0-2i \] -
这时我们得到了两个复平面坐标(0,2)和(0,-2),他有两个解。具体采用哪个取决于你想要干什么,它代表方向,正数是正常的方向也就是电流或电压从电源正极出发的方向,负数是和正常方向相反的方向。
在我们上面的求复数解过程中你可能会疑问0和1是哪里来的,事实上大部分的算式几乎都不能完美的吻合方程的一般形式,如一元二次方程的形式是:
当我们面对一些方程时它可能并不会配合我们长成这样,所以我们需要靠交换律和结合律将其简化,其实这才是方程最难的一步,简化和变换等式完全凭借你的知识积累还有感觉和视觉,尤其是面对一些复杂的方程时,直觉和洞察力,丰富的积累甚至毅力都很重要。
例如在复数解那个公式中并不满足一元二次的一般形式,所以我们实际上是将
变换成
变换后的公式满足了一般的一元二次形式所以可以直接套公式解。至于多加的那个"0x",因为他实际上并不存在,而且0乘以任何数都得0,所以我们可以直接将其省略掉,并不会破坏等式,这就是一种最简单的变换。
到此为止你就基本可以理解方程了,剩下的遇到什么一元n次,n元n次直接去网上找公式即可。当然了,如果你真的对方程感兴趣,被数学吸引,觉得套公式太简单也可以了解方程的底层原理去手动撸解。
联立方程
关于联立方程是什么我们已经在前面讲过,这里不在重复了。
矩阵与行列式
假如我们有一个方程组
上面这个联立方程我们就可以使用矩阵的写法就是
- 这个矩阵的意思是左面方框的第一行是多项式第一行是x+y的系数,也就是9和1,
- 这里我们又用到了变形,因为第一行的y没有系数所以我们用1*y结果还是y,等式也就没有被破坏,然后采用1作为y的系数,之后简单的变形不会再提示。
- 左面方框第二行是方程组第二行的系数。
- 然后我们把未知数放到矩阵中间的方框里
- 最右面的方框就是每个方程的结果
我们以后将左边的方框称作“系数矩阵”
- 它每一行代表一个方程
- 每一列代表一个未知数的系数
中间的方框称作“列向量”
- 它包含整个方程组的所有未知数
右边的同样叫做"列向量"
- 它包含每个方程的结果
我们这里说的向量其实就是之前在三角函数章节提到的矢量,在电路领域我们想要求一个方程组一般都是求电压或是电流,我们把xy放在方框里,这个方框就代表着未知的矢量。方框内的x和y同时代表着相量图的xy轴同时也代表着复平面的Re、Im轴。y的具体数值,也就是相量图或复平面的某个坐标点。有了这个坐标点我们就可以求出交流电的幅角或者说是相位还有它的电流电压大小和其他东西,总体就是这么个思路。
但是单靠矩阵我们解不出方程,所以我们需要配合行列式
考虑到当前字数篇幅有点多我把这一章分为上下两部分,行列式和具体的运算我们将在下章学习。