代数系统部分总结
前言:
本节的重点在于掌握二元关系的相关概念,群的相关概念,主要的题型有计算运算表中的幺元、零元,证明某二元运算符合结合律,证明某代数系统为群,判定子群等。
目录:
- 二元运算及其性质
- 代数系统
- 群与子群
二元运算及其性质
- 设S为集合,函数f :SxS→S称为S上的二元运算,简称为二元运算.
验证一个运算是否为集合S上的二元运算主要考虑以下两点:
1. S中任何两个元素都可以进行这种运算,且运算的结果是唯一的.
2. S中任何两个元素的运算结果都属于S,即S对该运算是封闭的.
-
设S为集合,函数f :S→S称为S上的一元运算,简称为一元运算.
-
设o为S上的二元运算,如果对于任意的x,y,z∈S都有
x o y=y o x
则称运算o在S上是可交换的,或者说运算○在S上适合交换律.例如,实数集上的加法和乘法是可交换的,但减法不可交换. -
设o为S上的二元运算,如果对于任意的x,y,z ∈S都有
(x o y)oz=xo (y o z)
则称运算○在S上是可结合的,或者说运算○在S上适合结合律. -
设o为S上的二元运算,如果对于任意的x∈S都有
XoX=x
则称该运算o适合幂等律. -
单位元

-
零元

-
逆元

运算关系:
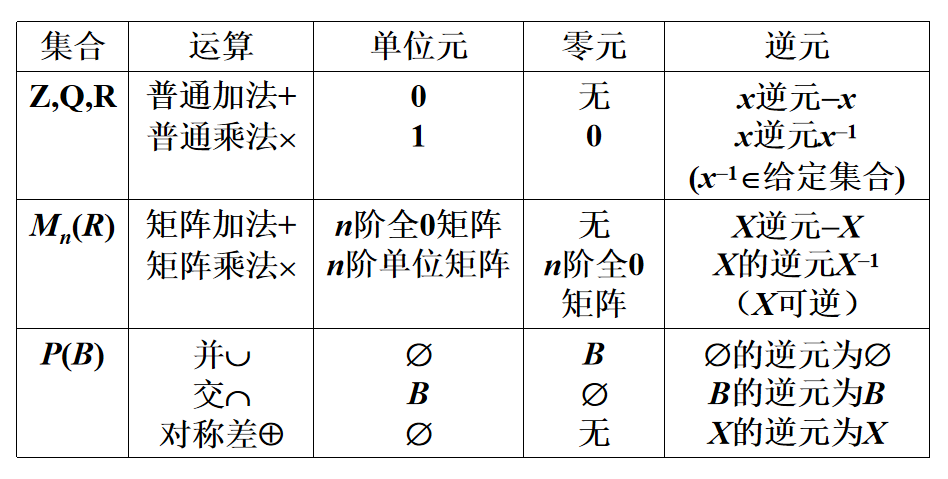
例题: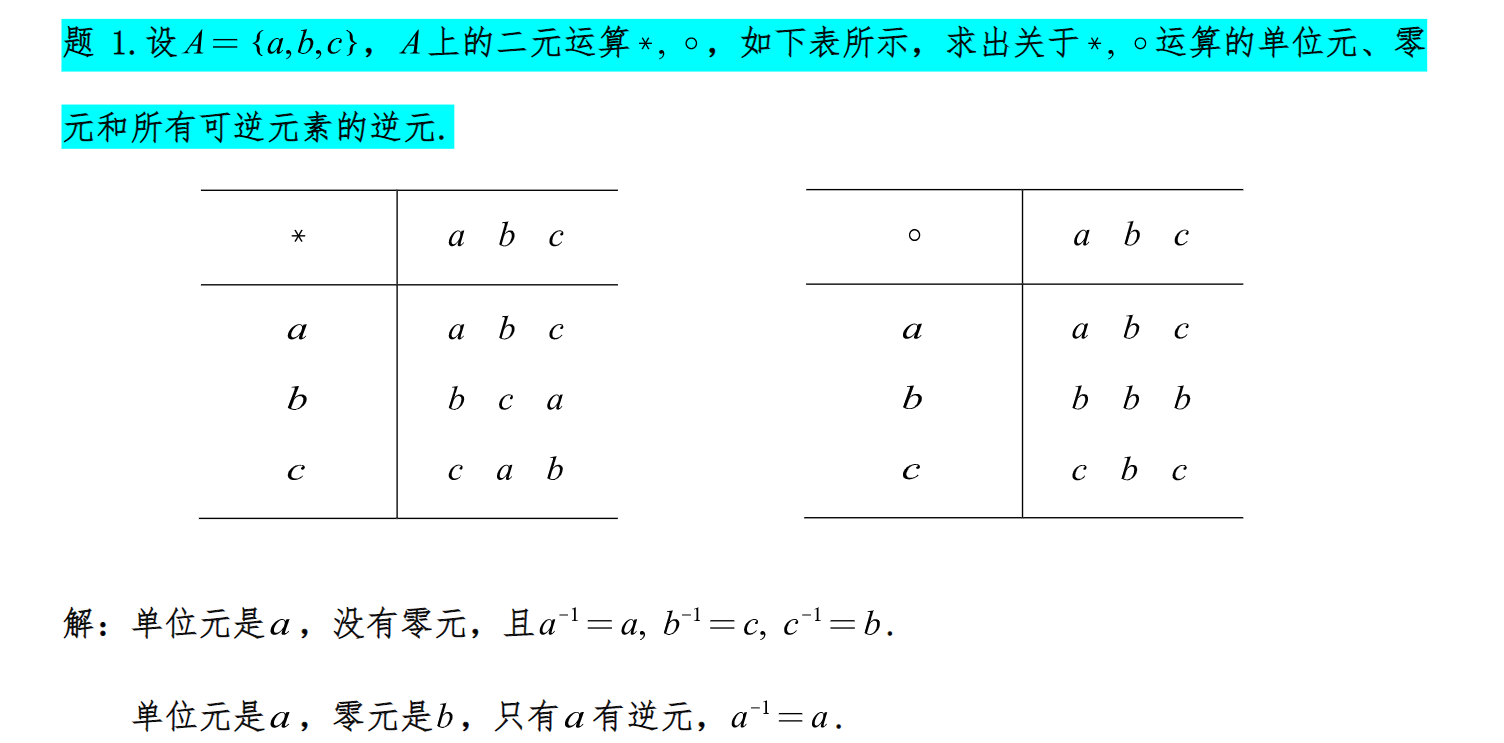
代数系统
-
定义:设A是一个非空集合,1,2,… ,r是代数运算,称集合A和代数运算1,2,… ,r所组成的结构为代数系统,记作U = <A,1,2,… ,*r > ,集合A称为代数系统的定义域(Domain).
当A为有限集时,称U为有限代数系统. -
在任意集合S的幂集P(S)中,考虑集合的补“",并“U"和交“∩”运算,则〈P(S),,u ,∩〉构成一个代数系统.这个系统称为集合代数.
-
设有代数系统U=<A,1,2,… ,r > ,X是A的非空子集,若运算1,2,… ,r在X上是封闭的,则称代数系统V=〈X,1,2,… ,r〉是U的子代数,同时称U是V的扩大.若X是A的真子集,则V为U的真子代数.
群与子群
一.群的基本概念:
-
一个代数系统<S,>,其中S是非空集合,是S上的一个二元运算,如果运算是封闭的,则称代数系统<S,>为广群.
-
一个代数系统<S, >,其中S是非空集合,是S上的一个二元运算,如果
a)运算是封闭的.
b)运算是可结合的,即对任意的x,y,z∈S,满足(x * y)* Z=X* (y * z),
则称代数系统<S,*>为半群. -
含有幺元的半群称为独异点.
-
给定一个代数系统<G,>,若运算满足:
封闭,结合,存在幺元,对于任意一个集合中的元*都有逆元,则称<G,*>是一个群,简称G是一个群,
称|G|(群G的基数)为群G的阶,如果G中的二元运算是可交换的,则称G为交换群(阿贝尔群). -
只含单位元的群称作平凡群
-
元素的阶: 设G是群,a∈G,使得等式 ak=e 成立的最小正整数 k 称为a 的阶,记作|a|=k,称 a 为 k 阶元. 若不存在这样的正 整数 k,则称 a 为无限阶元.
例题:

二.子群:
-
子群: 设(G,)是群,H是G的非空子集,如果(H,)是一个群,则称(H,)是(G,)的子群。
-
平凡子群: ({e},)、(G,)
-
非平凡子群: (H*)且H≠{e},G(又称真子群)
子群的判定定理:
- 根据定义:(1)非空子集、(2)封闭性、(3)结合律、(4)单位元、(5)逆元
- 判定定理1: H是群G的非空子集,对于任意a,b ∈ H,都有a * b-1 属于 H,则H是G的子群。
- 判定定理2: H是群G的非空子集,如果H是有限集,而且G的运算*在H上满足封闭性,则H是G的子群。