Lecture09-Mesh Representation &Geometry Processing-网格表示与几何处理

Mesh Presentation网格表示

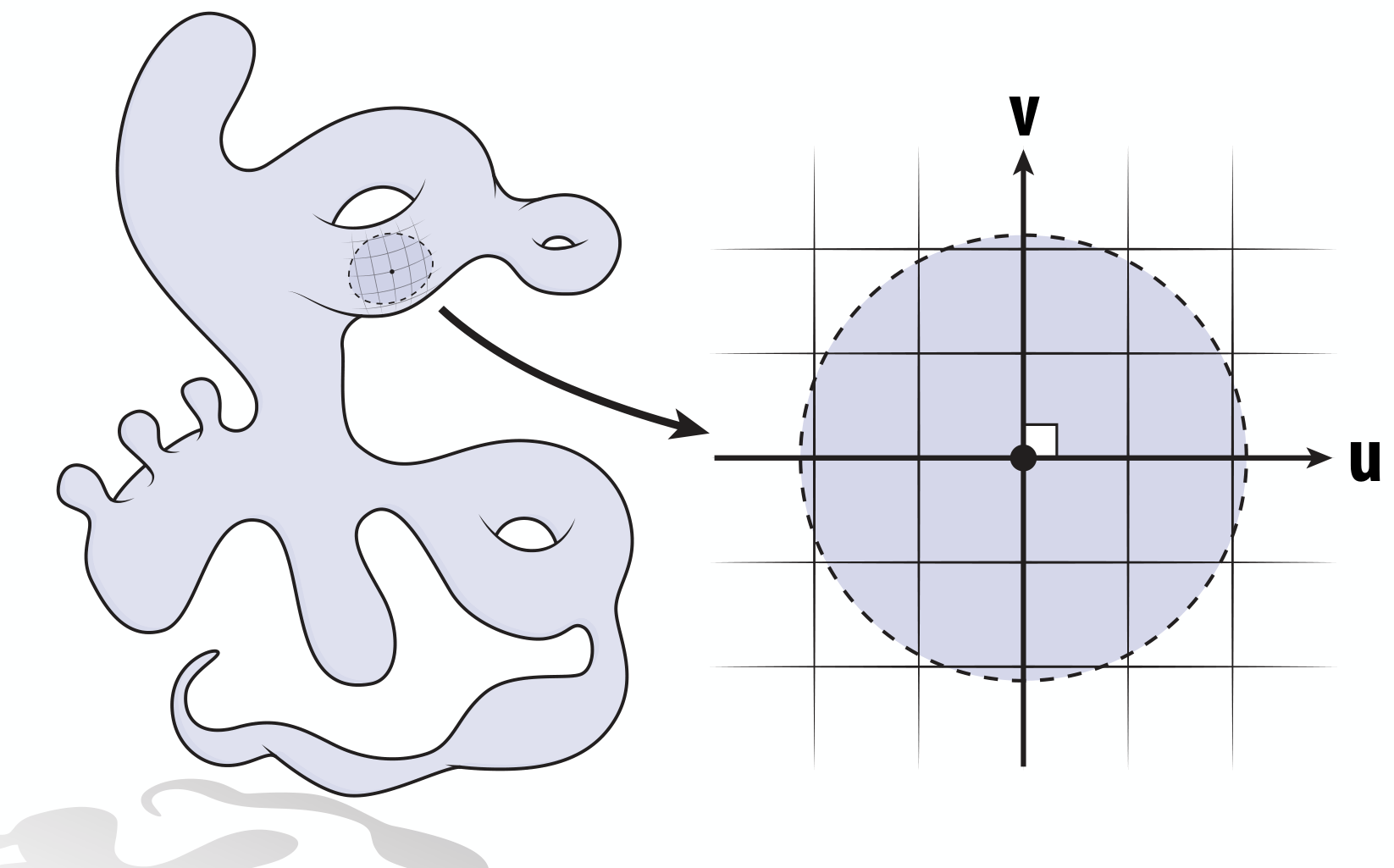
这种局部具有欧几里得性质的几何对象（严格地说：要每个点都存在一个和 \(n\) 维欧式空间同胚的邻域），就叫做流形Manifold啦（？好像没毛病但又哪里怪怪的，为什么这里要扯这玩意）

位图（bitmap images）：为了对图像进行编码，使用规则的像素网格，但是对于一些基本单元不是小方格的情况，效果可能不太好。
so为什么要用规则的网格（regular grid）呢？——Regular grids make life easy！（？？）
- 1、更简单高效，比如每个点的领域只有4个格子，标号和存储也非常方便。
- 2、基本上可以编码任何图像
但是规则的网格是位图最好的选择吗！！！
- 并不是！可能有些不太好的结果，比如各向异性，不能捕获边缘（它在说什么？）

Smooth Surfaces光滑曲面

光滑曲面是流形，但并不是所有形状都是流形！比如下图中间那个点，不管怎么取领域都不会有欧式性质。

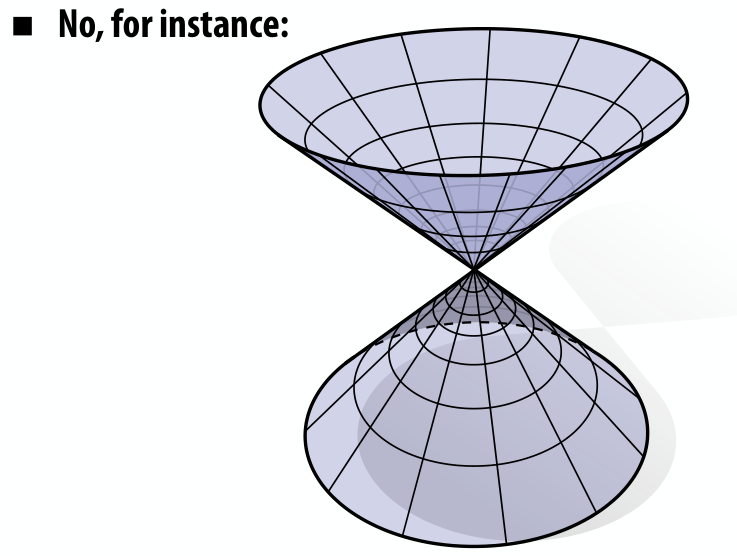
怎么判断简单多边形构成的图形是不是流形？有很简单的判断方式：

每条边只出现在两个多边形内，即不能有“鳞”（fins）
对每个顶点，包含它的多边形构成“扇形”（fans）

为什么流形这么重要呢？——可以保证数据结构和算法简单高效。

如何编码？数组、链表、块状链表（bushi）

Polygon soup-多边形汤

注：“汤”似乎是用来形容这种“无组织”的方式。

基本观点
- 每个三角形只存储三个点的坐标。
- 没有关于连通性的信息。

Adjacency List-邻接表

（你管这玩意叫邻接表？）

用一个矩阵存结点的坐标，比如：

\[\begin{matrix} & x & y &z\\ 0:&- 1& -1 &-1\\ 1:& 1& -1& 1\\ 2:& 1 &1 &-1\\ 3:& -1 &1& 1\\ \end{matrix} \]

然后紧接着的问题是，如何快速查找所有和某个点（比如2号点）相邻（有公共边）的点？

Incidence Matrix-关联矩阵

Q：如果要快速回答“领域查询”要怎么办呢？

A：简化邻接表的存储方式！就是再用一个关联矩阵来存放信息：

\[\begin{matrix} & v0 & v1 & v2 & v3\\ e0 & 1 & 1 & 0 & 0\\ e1 & 0 & 1 & 1 & 0\\ e2 & 1 & 0 & 1 & 0\\ e3 & 1 & 0 & 0 & 1\\ e4 & 0 & 0 & 1 & 1\\ e5 & 0 & 1 & 0 & 1\\ \end{matrix} \]

当然很明显这样会有资源浪费，只有\(2\times |E|\) 个信息是有用的！所以课件就说用稀疏矩阵（sparse matrices）来存！

这样做的优缺点就很明显了，存储非常浪费，并且不太支持动态修改，但是查询是 \(O(1)\) 的。

Half-Edge Data Structure（Linked-list-like）-半边数据结构（类似邻接表）

即，把一条边拆成两条边

存储邻域信息
*twin指向这条边对面的半边，*next表示下一条的半边，*edge,*face 指向所在的边和面。

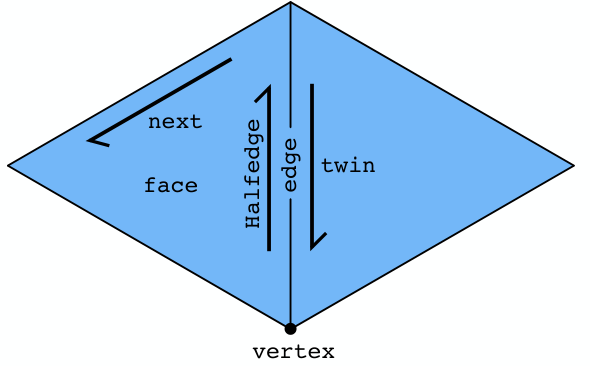
进一步，每个点、线、面的信息，其实也只需要存储“半边”——对于边来说，可以用twin访问，面的话可以一直跳next

struct Halfedge{
    Halfedge* twin,* next;
    Vertex* vertex;
    Edge* edge;
    Face* face;
};
struct Edge{
	Halfedge* halfedge;
};
struct Face{
	Halfedge* halfedge;
};
struct Vertex{
    Point pt;
    Halfedge* halfedge;
};
//它这里似乎认为一个“点”vertex，是

很明显，对于网格图，这种半边数据结构能够很方便遍历。

遍历一个面：

Halfedge* h = f->halfedge;// f: face 
do {
    process(h->vertex);
    h = h->next;
}
while( h != f->halfedge );

遍历一个点周围的边：

Halfedge* h = v->halfedge;// v: vertex
do {
    process(h->edge);
    h = h->twin->next;
}
while( h != v->halfedge );

接着说，这种半边数据结构基本是“流形”，以及edge,face,vertex 的信息其实是可以隐藏起来的——真正要访问整个mesh，只需要*next,*twin两个信息：

沿着next转一圈，得到整个face。
沿着twin走，得到这条边。
沿着next->twin，得到一圈的顶点。

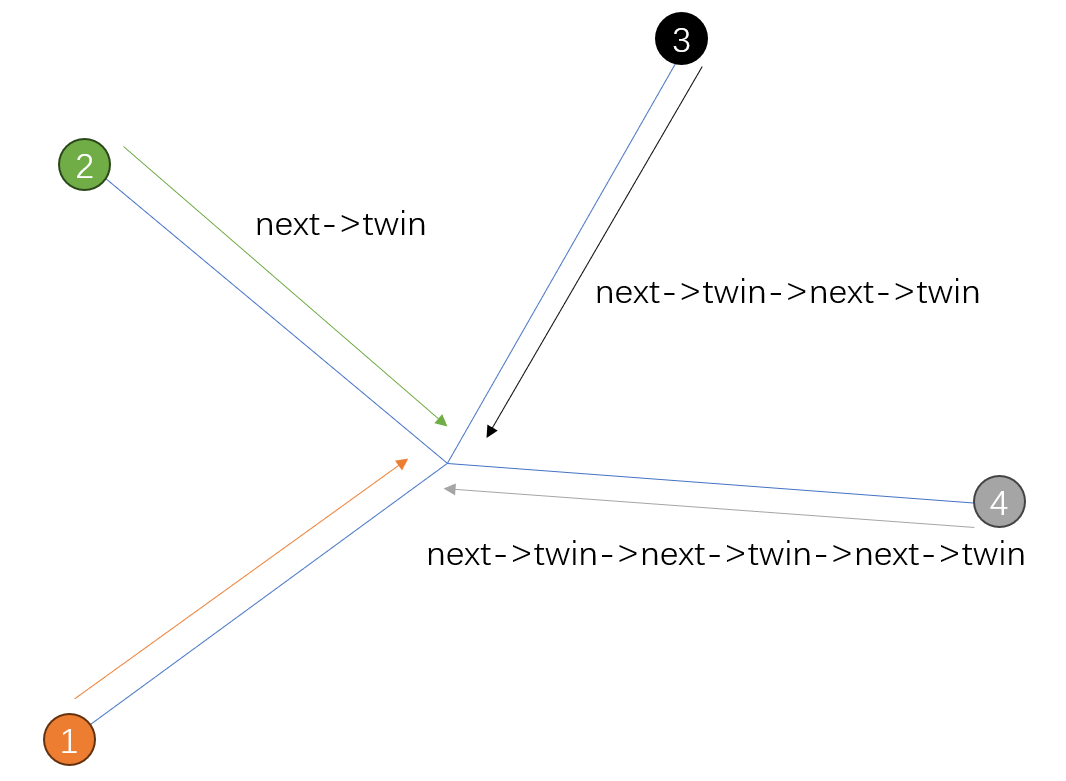
Q：如何表示一些不是流形的图像？（好像没给回答）

Half-Edge meshes are easy to edit

对于三角形网格，一些可能的原子/基本操作（atomic operation）：翻转、分裂、坍缩

如何去分配（Allocate？）/删除一个元素，或者重新分配指针？需要非常小心地去保持流形的性质！！（这要你说？）

这三个操作课件也只是bb了一下有哪些操作，应该不需要在意具体细节：

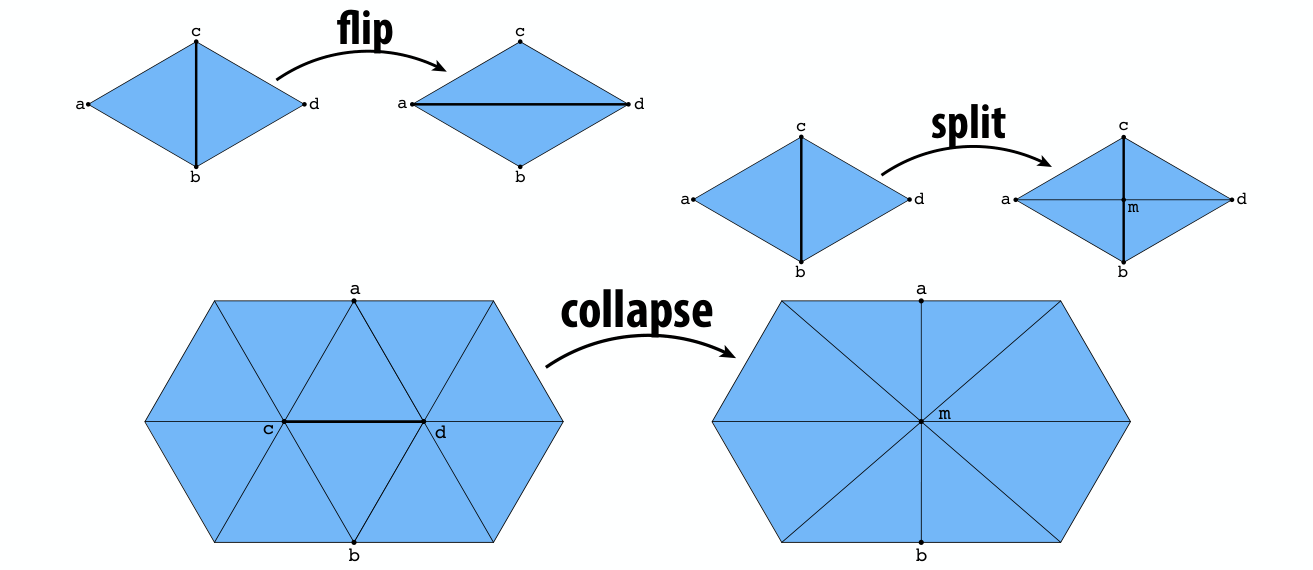
Edge Flip（Triangles）边的翻转

\((a,b,c),(b,d,c)\to (a,d,c),(a,b,d)\)，没有元素的创建/删除，但是要改很多指针…

Edge Split（Triangles）边的分裂

需要添加一个新的边\((a,d)\)，同时 \((c,b)\) 中间也多了个新的点 \(m\) 需要拆开。

Edge Collapse（Triangles）边的坍缩

把 \((b,c)\) 边变成一个点 \(m\) ？然后删除一些元素（应该是\((c,d),(a,c)\)），以及一些指针的修改。

Geometry Processing 几何处理

扩展传统的数字信号处理（音频、视频等）以处理几何信号：

上采样/下采样/重采样/滤波…
混叠（？没懂这是啥，aliasing）

（然后这里开始说一些实际应用的场景了，应该不太重要）

重建：给一个几何图形的样本，重新构建表面；
- 这个样本可能是什么样的？有很多可能：点、点&法线、曲线密度积分…
- 如何得到表面，也有很多种技术：基于轮廓线、基于Voronoi图、还有PDE和Radon变换
上采样：通过插值提升分辨率！
- 对于图像（image）：比如通过双线性，双三次插值（bilinear, bicubic interpolation）
- 多边形网格：：细分（subdivision），双边上采样（bilateral upsampling）
下采样：降低分辨率，并且最好能保持形状。
- 对于图像：最近邻域/双线性/双三次插值
- 点云：二次采样（subsampling）——取更少的点
- 多边形网格：迭代抽取、形状近似
重采样：修改采样点的分布，以提升质量。
- 多边形网格：保持多边形非常重要！不同的任务有不同的“质量”的概念…
- 比如：可视化/解方程（可能对于质量的需求就不一样？）
滤波：去除噪声、或者突出图像的重点特征
- 图像：模糊化、双边滤波器（？）、边缘探测
- 多边形网格：曲率流（？）、双边滤波器、分光滤波器
压缩：通过去除冗余信息（或者几乎不重要的信息），减少存储的大小
- 图像：1、哈夫曼编码、运行长度（run-length不懂咋翻译）——无损的！2、余弦/小波（JPEG/MPEG）——有损的
- 几何网格：压缩与连通性（？），有很多技术
形状分析：识别/理解重要的语义特征
- 图像：计算机视觉…
- 多边形网格：分割、对应、对称检测

Geometry ProcessingTasks: 3 Examples

细分、简化、标准化

Subdivision Surfaces 细分曲面

从一个粗糙的多边形网格开始：细分每个元素，再通过局部平均，更新顶点。
很多可能的规则：Catmull-Clark (四边形)、Loop (三角形)
共同的问题：插值还是近似？在顶点处连续？（保持连续性很难的啦！）

Loop Subdivision 循环细分

关于这个算法更多的细节：https://blog.csdn.net/McQueen_LT/article/details/106136324

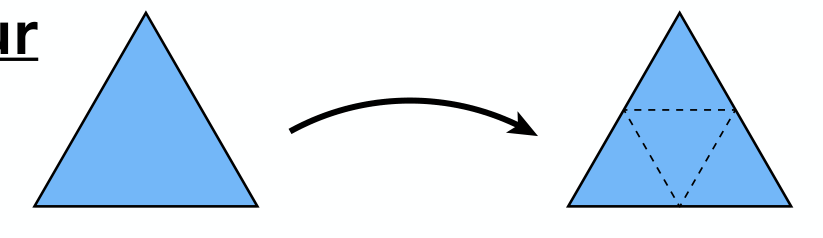
大体思路是把每个三角形分成四个，按照权重分配新的点，那么通常有一边上的新点，被两个面所共享，所以就有了Loop细分的规则：按照 \((1/8,1/8,3/8,3/8)\) 的系数分配：

那么对于老的（old）顶点呢？设这个顶点度数是 \(n\) ，给周围的（老的）点分配 \(u\) 权值，给自己分配\(1-nu\)：

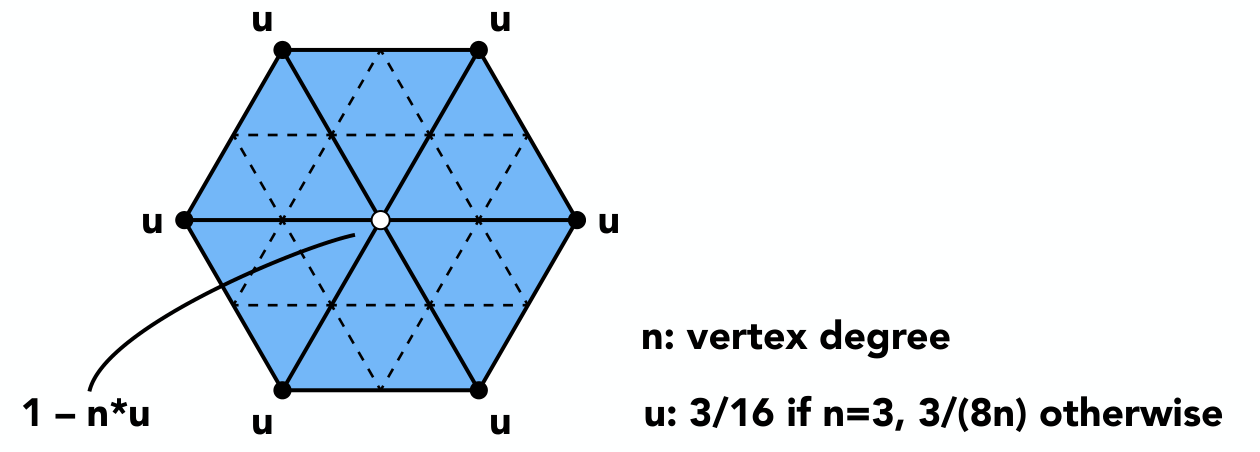
（“为什么叫Loop细分啊？“”Loop是人名“”草w“）

Catmull-Clark Subdivision (Regular Quad Mesh-普通四边形网格)

参考资料：https://en.wikipedia.org/wiki/Catmull–Clark_subdivision_surface

（Catmull是2019年图灵奖得主之一）

Loop细分只能解决三角形网格的细分，对于一般情况用Catmull-Clark细分

（注：课件上的图片总让人感觉看着像一个平面…看着让人误以为边点在边上…其实应该是空间里的图形，边点也不一定在边上）

面点（face point）：每个面顶点的平均值
边点（edge point）：一条边连接的两个面的面点 \(f_1,f_2\) ，以及两个顶点 \(v_1,v_2\)，则边点 \(e=(f_1+f_2+v_1+v_2)/2\)
中点（midpoint）：就是正常的中点，这里就是在强调midpoint和edge point不是同一个东西
原式顶点点（old "vertex" point）：字面意思

对于每个原式顶点点 \(p\) ，最后更新的顶点：

\[v=\frac{\bar{f}}{n}+\frac{2\bar{m}}{n}+\frac{n-3}{n}p \]

\(\bar{f}\) 是和\(p\) 相邻的面点的均值， \(\bar m\) 和 \(p\) 相邻的中点的均值，\(n\) 则是点 \(p\) 的“价”（valence）（这玩意好像就是度数degree？）。

好了，然后看课件发现，咦我边点怎么没用的样子？

好像课件确实没提，因为步骤其实是这样：

1、求出面点、边点、新的顶点坐标。
2、每个面的面点连接边点，每个（新的）顶点再向对应的边点连边
如下图（蓝色是面点，粉色是边点，绿色是新点）：

然后再回过头看课件，对于最简单的四边形网格（Regular Quad Mesh），每次做Catmull-Clark细分就只是给网格多划了几刀。然后对于一个一般的例子：

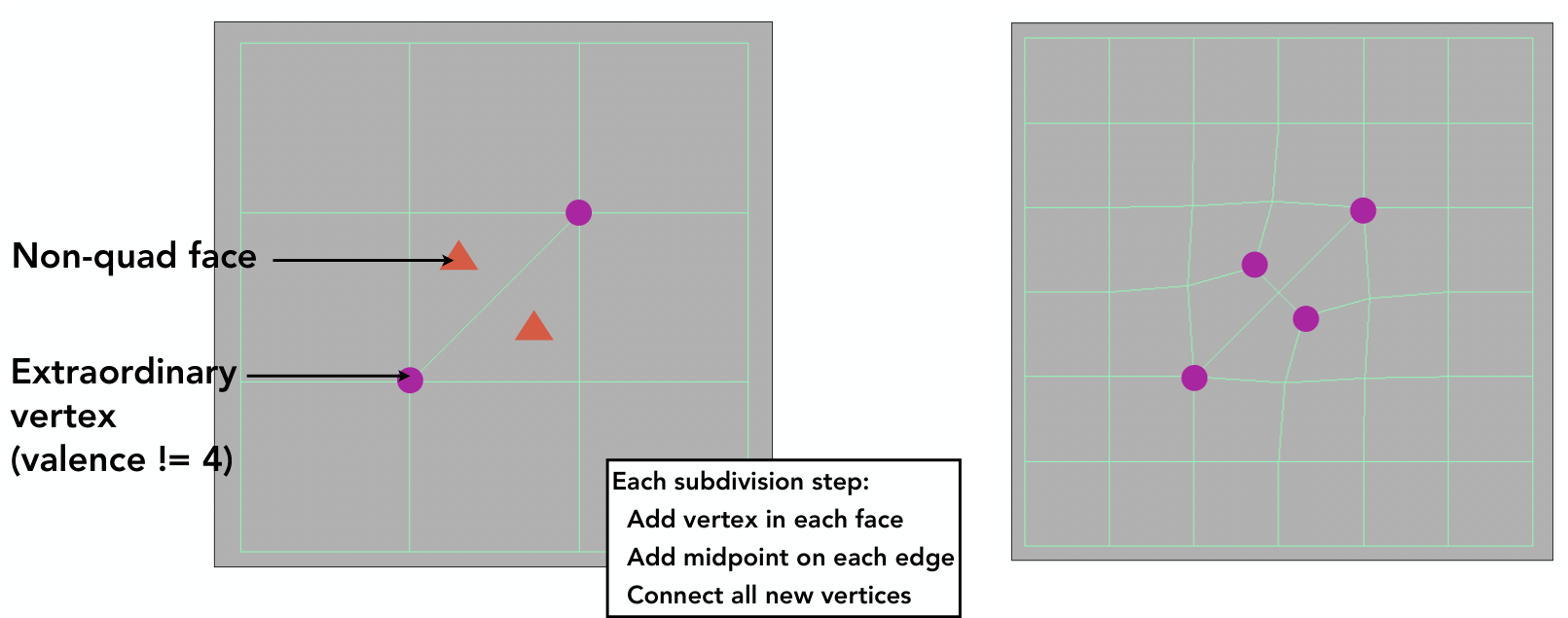
这里是8个正方形，以及2个三角形。

新加入的橙色三角形就是面点，然后在边上取中点（感觉应该是边点？）连接，以及新的结点照样计算，就连出来右边的效果。

Q：为什么细分之后，其他正方形也歪了？
A：想想很正常，\(v=\bar{f}/3+2\bar{m}/3\)，因为有三角形，这时候面点已经不是正中心了，所以 \(v\) 歪一点就不奇怪了。
Q：细分之后有多少奇异点？（extraordinary vertices）他们的价是多少？有多少非四边形的面？
A：首先非四边形的面细分之后是没了（因为我们的连接方式连完之后都是四边形，除非有退化的情况？），而奇异点的个数不会变少，而每次细分后，奇异点增加的个数=细分前非四边形的面数，是不是和平面图转对偶图有异曲同工之妙。

后面提了一嘴，Catmull-Clark算法在三角形上跑的效果似乎不太好，有很多不规范的点，然后也有锯齿。

网格简化

需要去决定修改（坍缩）哪些边，进一步考虑去分析：坍缩一条边之后，会有多少几何误差？二次误差度量（quadirc error matric）！

对每条边，考虑：假设坍缩这条边，得到的图形，所能得到的最小误差（坍缩之后得到一个点，这个点到其他面的距离平方）是多少？每次贪心地选择误差最小的；同时坍缩掉一条边之后，会影响一些已经存在的边，所以还要去更新一些边的答案，所以说要用优先队列维护。
注意：这里的贪心并不保证全局最优，只不过是根据经验来说比较优…
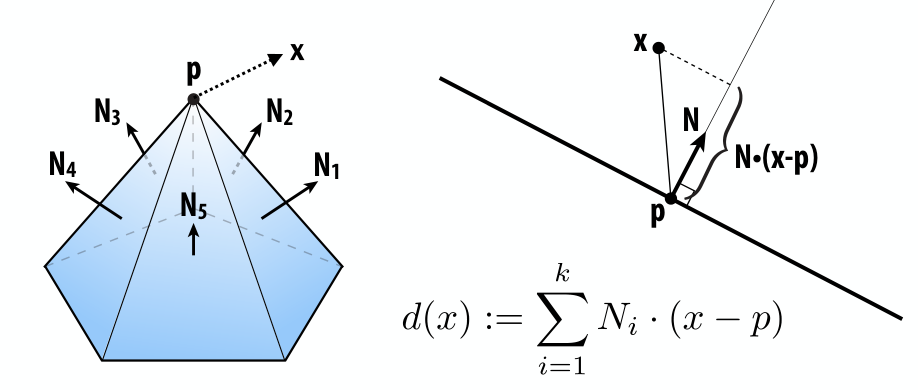
然后这里课件上用的”二次度量误差“其实也不是严格的距离，而是说假设坍缩之后的点从 \(p\) 移动到 \(x\) ，那么到每个面的距离用点积来近似，所以就变成求 \(\sum N_i\cdot (x-p)\)的最小值。