蒟蒻自学的 \(\text{Splay}\)，说的不好的地方还请指出qwq

那么进入正题：

\(\text{Splay}\) 的概念及基本实现

1. \(\text{Splay}\) 简介

\(\text{Splay}\) 树，是一种二叉搜索树，它能在 \(O(\log n)\) 的（均摊）时间复杂度内完成插入、查找和删除操作。它由 Daniel Sleator 和 Robert Tarjan (怎么又是Tarjan) 在1985年发明。

那么我们首先来了解一下什么是二叉搜索树：

二叉搜索树，又称二叉排序树，二叉查找树，一棵二叉查找树具有如下性质：\((\text {from OI-wiki})\)

1. 空树是二叉搜索树。

2. 若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。

3. 若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。

4. 二叉搜索树的左右子树均为二叉搜索树。

例如，这就是一棵合法的二叉搜索树：

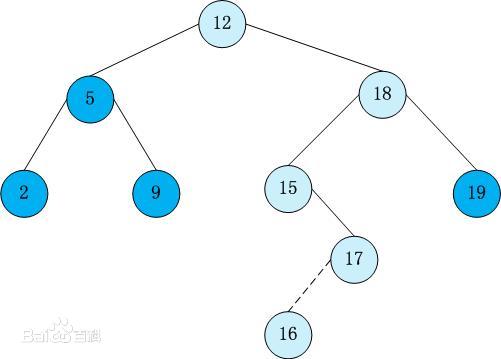
（图源：百度百科）

二叉搜索树的每个节点需要维护以下几个值：

struct Node
{
    int val;     //节点的权值
    int cnt;     //权值出现个数
    int sz;      //子树大小
    Node *fa;    //父亲
    Node *ch[2]; //左右儿子
    Node() {
        val = cnt = sz = 0;
        fa = ch[0] = ch[1] = nullptr;
    }
}

很明显，利用二叉搜索树的性质，当查找一个数时，若比当前节点大就向右子树查找，比当前节点小就向左子树查找，这种二分的思想很大可以提高查找效率

因此，若二叉搜索树的高度为 \(h\) ，则插入、删除、查找元素的时间复杂度均为 \(O(h)\)

期望情况下，\(h=\log n\)，也就是说，朴素的二叉搜索树的期望复杂度是 \(O(\log n)\)

但在一些极端数据下，如 \(1,2,3\dots 99999,100000\) 二叉搜索树就会退化成一条链，使 \(h=n\) ，从而使复杂度达到上界，即 \(O(n)\)

因此，维护二叉搜索树的平衡，换句话说，就是使树高 \(h\) 始终与 \(\log n\) 接近，就能使复杂度始终为 \(O(\log n)\)，\(\text{Splay}\) 就是为了实现这个而被发明的

与其他平衡树相比，\(\text{Splay}\) 的优缺点：

• 优点：通过不断调整自身维护平衡，不需要维护其它无关元素。 代码更短（基本操作就一个其他平衡树大多都有的旋转和一个函数体4行的splay操作）

• 缺点：常数较大。 复杂度是均摊的，不支持可持久化

节点基本操作：

每个节点有以下三种基本操作（不用我讲了吧）：

//清空节点
void clear() {
    val = cnt = sz = 0;
    fa = ch[0] = ch[1] = nullptr;
}

//更新 sz
inline void upd() {
    if(!this)return; //防止空指针发生段错误
    sz = (ch[0] ? ch[0]->sz : 0) + (ch[1] ? ch[1]->sz : 0) + cnt; 
}

//返回此节点是父亲的左儿子还是右儿子
inline int get() { 
    return this == fa->ch[1]; 
}

而整棵树需要维护的是 \(N\) 个节点和两个指针，以及两个错误变量（后面会用到）：

class SplayTree{
    Node nd[N];
    Node *tot; //最后一个节点的指针
    Node *rt;  //根节点指针，是Splay所需要的
    static Node no_pre, no_nxt;//后面讲
    public:
    SplayTree() {
        tot = nd;
        rt = nullptr;
        no_pre.val = -2147483647;
        no_nxt.val = 2147483647;
    }
}

2. \(\text{Splay}\) 基本概念：旋转

旋转 （这个名字似乎不怎么形象） 本质上其实是将节点与其父亲的位置互换，并保证互换后生成的树仍是一棵二叉搜索树。与其他平衡树不同的是，\(\text{Splay}\) 是使子节点成为父节点（向上），而如 \(\text{RB、AVL}\) 等是使父节点成为子节点（向下）。

下图就是将 \(2\) 号节点右旋的例子：

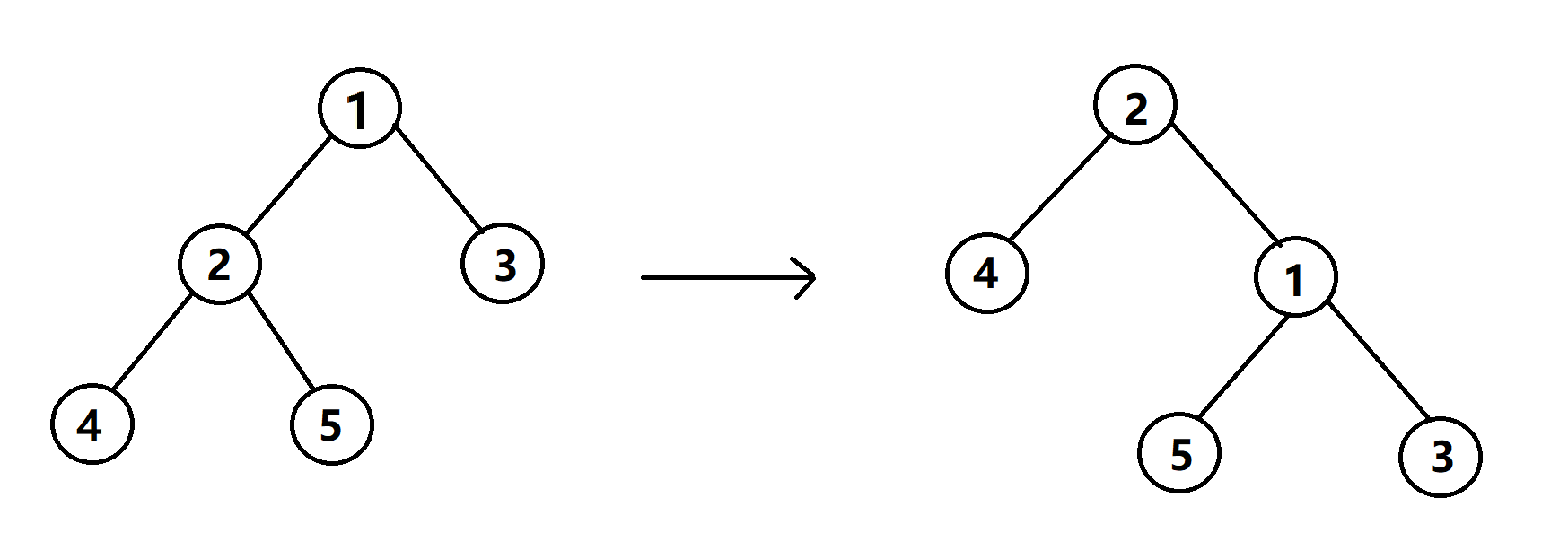
可以看出，将 \(2\) 号节点右旋，就是让它的父亲 \(1\) 号节点成为它的右儿子，而同时为了使旋转后仍是一棵二叉搜索树，需要将 \(2\) 号节点的右儿子变成 \(1\) 号节点的左儿子，而如果 \(1\) 号节点还有父亲，就让 \(2\) 号节点代替 \(1\) 的位置，成为它爷爷的儿子（看不懂就结合以一下代码）

而左旋也同理，下图就是将 \(1\) 号节点左旋的例子：

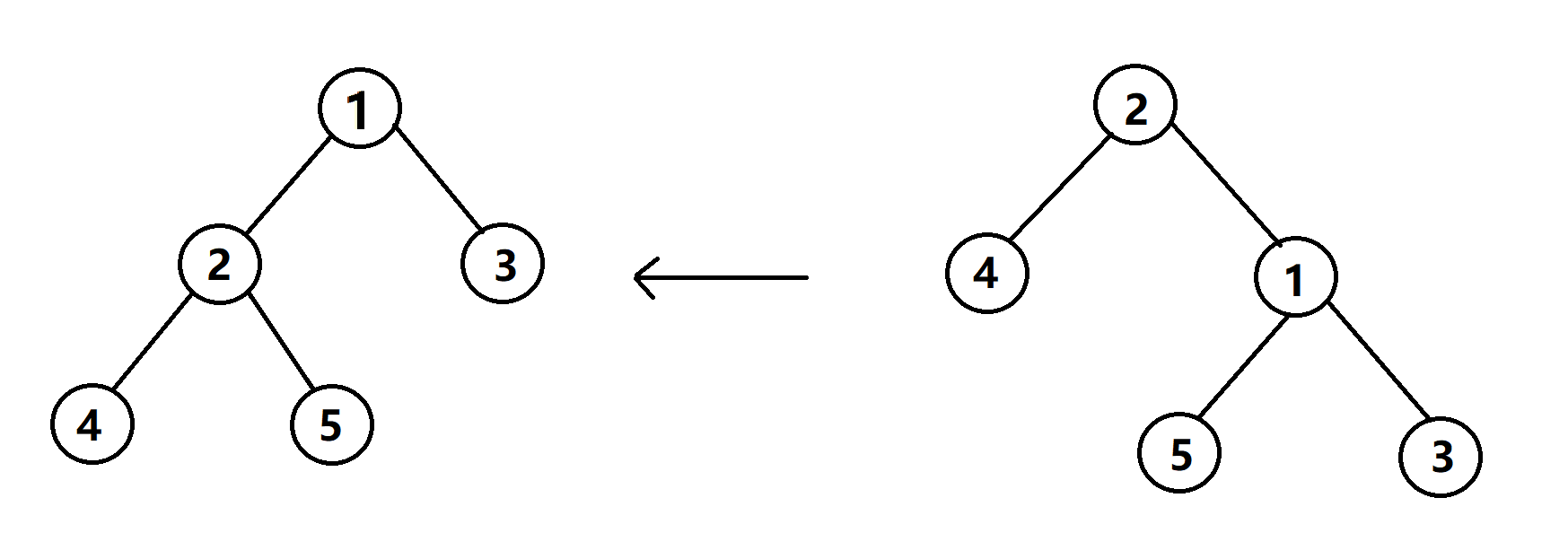
代码：（ Node 的成员函数）（注释是以右旋为例）

inline void rotate() {
    int chk = get();
    Node *_fa = fa, *grd = fa->fa; //暂存原父亲和爷爷
    fa->ch[chk] = ch[chk ^ 1];//原父亲的左儿子换成this的右儿子
    if (ch[chk ^ 1])//如果有右儿子的话
        ch[chk ^ 1]->fa = _fa;
    ch[chk ^ 1] = _fa;
    _fa->fa = this;//让原父亲成为this的右儿子
    fa = grd;//变成爷爷的儿子
    if (grd)
        grd->ch[_fa == grd->ch[1]] = this; //如果原父亲还有父亲，将此节点的父亲更新为爷爷并把爷爷的儿子改指向此节点
        //注意这里不能写-fa->get()，因为它的父亲已经被更新了，不再是this的爷爷
    _fa->upd();
    upd(); //分别更新
}

3. \(\text{Splay}\) 操作

\(\text{Splay}\) 的目的是将当前节点旋转到根节点

考虑以下几种情况：（其中 \(x\) 为需要旋转到根的节点）

如果 \(x\) 的父亲是根节点，直接将 \(x\) 旋转。

如果 \(x\) 的父亲不是根节点，且 \(x\) 和父亲的儿子类型相同，首先旋转其父亲，然后将 \(x\) 旋转

如果 \(x\) 的父亲不是根节点，且 \(x\) 和父亲的儿子类型不同，将 \(x\) 旋转两次

（图源：OI-wiki）

重复以上操作，直至 \(x\) 为根节点（没有父亲节点）

其实我们一直旋转 \(x\) 也可以使 \(x\) 到达根节点，为什么还要这么麻烦呢？因为\(\text{Splay}\) 的目的正是改变树的结构，维护树的平衡，而 只旋转 \(x\) 并不能改变树的结构 我们一般把这种不看父亲只旋转自己的叫做Spaly

代码：( SplayTree 的成员函数)

//Splay 操作，将 now 节点旋转至根节点
void splay(Node *now) {
    for (Node *fa = (now->fa); (fa = (now->fa)); now->rotate())
        if (fa->fa)
            (now->get() == fa->get() ? fa : now)->rotate();
    rt = now;
}

理解了基本操作之后，我们来试着实现洛谷P3369里的需求：

4. 判断元素是否存在

利用二叉搜索树的性质，查找一个元素 \(x\) 的步骤如下：

1. 从根节点开始搜索

2. 如果 \(x\) 等于当前节点的val，则 \(x\) 存在，将此节点 \(\text{Splay}\) 并返回true

3. 如果当前节点为空（不存在），则 \(x\) 不存在，返回false

4. 如果 \(x\) 小于当前节点的val，则向其左子树查找；如果 \(x\) 大于当前节点的val，则向其右子树查找

5. 回到步骤2

代码：

bool exist(int x) {
    Node *now = rt;
    while (now) {
        if (x < now->val)
            now = now->ch[0];
        else if (x > now->val)
            now = now->ch[1];
        else if (x == now->val)
            return splay(now), 1;
    }
    return 0;
}

5. 插入元素 \(x\)

对于插入操作，有以下几种情况：

1. 如果树空了，则直接插入根并退出。

2. 如果已经有节点的值为 \(x\)，则将此节点cnt++，并更新sz

3. 如果查找不到 \(x\)，则将最后找到的空节点里插入此值

（不要忘记 \(\text{Splay}\)）

void insert(int x) {
    if (!rt) { //如果树空了，则直接插入根并退出
        rt = ++tot;
        rt->val = x;
        rt->cnt++;
        rt->sz++;
        return;
    }
    Node *now = rt, *fa = nullptr;
    while (now) {
        if (now->val == x) { //如果当前节点的权值等于 x 则增加当前节点的大小并更新节点和父亲的信息，将当前节点进行 Splay 操作。
            now->cnt++;
            now->upd();
            fa->upd();
            splay(now);
            return;
        }
        fa = now;
        now = now->ch[x > now->val]; //否则按照二叉查找树的性质向下找，找到空节点就插入，并进行 Splay 操作
    }
    //跳出了 while 说明没有值为 x 的节点，则在当前节点插入x
    now = ++tot;
    now->val = x;
    now->cnt++;
    now->upd();
    now->fa = fa;
    fa->ch[x > fa->val] = now;
    fa->upd();
    splay(now);
}

6. 查询 \(x\) 的排名

排名定义为小于 \(x\) 的元素个数加一

根据二叉搜索树的性质，显然 \(x\) 的排名就是值为 \(x\) 的节点的左子树大小加一

代码：

int rank(int x) {
    insert(x);//防止x不存在
    return del(x),(rt->ch[0] ? rt->ch[0]->sz : 0) + 1;
}

7. 查询排名为 \(k\) 的数

设 \(k\) 为当前子树里的排名，则有以下两种情况：

1. 如果左子树非空且当前树里的排名 \(k\) 不大于左子树的sz，那么向左子树查找。

2. 否则将 \(k\) 减去左子树的和根的大小。如果此时的 \(k\) 小于等于 \(1\)，则返回该根节点的权值，否则继续向右子树查找。

int get(int k) { //k是当前子树里的排名
    Node *now = rt;
    while (now) {
        if (now->ch[0] && k <= now->ch[0]->sz) //如果左子树非空且当前排名 k 不大于左子树的大小 ，那么向左子树查找。
            now = now->ch[0];
        else {
            k -= now->cnt;
            if (now->ch[0])
                k -= now->ch[0]->sz; //否则将 k 减去左子树的和根的大小，得到在右子树中的排名
            if (k <= 0)
                return splay(now), now->val; //若 k 小于等于 0 ，说明 now 里的元素的排名是 k
            now = now->ch[1];                //在右子树中查找
        }
    }
    return -1;
}

8. 查询 \(x\) 的前驱

前驱定义为小于 \(x\) 的最大的数

查询 \(x\) 的前驱，需要先将 \(x\) 插入，此时 \(x\) 就是根节点， \(x\) 的前驱就是其左子树最右边的节点，最后删除 \(x\)

代码：（insert和del的部分在自己操作时做）

Node *pre() {
    Node *now = rt->ch[0];
    if (!now)//没有前驱
        return &no_pre;
    while (now->ch[1])
        now = now->ch[1];
    splay(now);
    return now;
}

9. 查询 \(x\) 的后继

后继定义为大于 \(x\) 的最小的数

查询后继与前驱同理，后继就是右子树中最左边的节点

代码：（insert和del的部分在自己操作时做）

Node *nxt() {
    Node *now = rt->ch[1];
    if (!now)//没有后继
        return &no_nxt;
    while (now->ch[0])
        now = now->ch[0];
    splay(now);
    return now;
}

10.删除元素 \(x\)

想要删除 \(x\) ，首先将值为 \(x\) 的节点旋转至根

然后考虑以下情况：

1. 如果不只有 \(1\) 个 \(x\) ，则将 \(x\) 的个数减一并退出

2. 如果只有 \(1\) 个 \(x\) ，且它的两棵子树均为空，则清空根节点

3. 如果只有 \(1\) 个 \(x\) ，且它只有一棵子树为空，则保留那棵子树，并清空原根节点

4. 如果只有 \(1\) 个 \(x\) ，且它的两棵子树均不为空，则将左子树的最大值旋转至根，并使原右子树成为它的儿子（合并左右子树）

void del(int x){
    if (!exist(x))
        return;
    if (rt->cnt > 1) {
        rt->cnt--;
        rt->sz--;
        return;
    }
    if (!rt->ch[0] && !rt->ch[1]) {
        rt->clear();
        rt = nullptr;
        return;
    }
    if (!rt->ch[0]) {
        Node *_rt = rt; //暂存原根节点
        rt = rt->ch[1];
        rt->fa = nullptr;
        _rt->clear();
        return;
    }
    if (!rt->ch[1]) {
        Node *_rt = rt; //暂存原根节点
        rt = rt->ch[0];
        rt->fa = nullptr;
        _rt->clear();
        return;
    }
    Node *_rt = rt; //暂存原根节点
    Node *left = pre();//左子树的最大值就是根节点的前驱
    _rt->ch[1]->fa = left;
    left->ch[1] = _rt->ch[1];//原右子树的父亲更改为左子树最大值
    _rt->clear();
    rt->upd();
}

最终代码：

#include <bits/stdc++.h>
#define N 100005
class SplayTree {
    struct Node {
        int val;
        int cnt;
        int sz;
        Node *fa;
        Node *ch[2];

        Node() {
            val = cnt = sz = 0;
            fa = ch[0] = ch[1] = nullptr;
        }

        void clear() {
            val = cnt = sz = 0;
            fa = ch[0] = ch[1] = nullptr;
        }

        inline void upd() {
            if (!this)
                return;
            sz = (ch[0] ? ch[0]->sz : 0) + (ch[1] ? ch[1]->sz : 0) + cnt;
        }

        inline bool get() { return this == fa->ch[1]; }

        inline void rotate() {
            int chk = get();
            Node *_fa = fa, *grd = (fa->fa);
            fa->ch[chk] = ch[chk ^ 1];
            if (ch[chk ^ 1])
                ch[chk ^ 1]->fa = _fa;
            ch[chk ^ 1] = _fa;
            _fa->fa = this;
            fa = grd;
            if (grd)
                grd->ch[_fa == grd->ch[1]] = this; 
            _fa->upd();
            upd();
        }
    } nd[N];
    Node *tot
    Node *rt;
    Node no_pre, no_nxt;
    void splay(Node *now) {
        for (Node *fa = (now->fa); (fa = (now->fa)); now->rotate())
            if (fa->fa)
                (now->get() == fa->get() ? fa : now)->rotate();
        rt = now;
    }
    bool exist(int x) {
        Node *now = rt;
        while (now) {
            if (x < now->val)
                now = now->ch[0];
            else if (x > now->val)
                now = now->ch[1];
            else if (x == now->val)
                return splay(now), 1;
        }
        return 0;
    }

public:
    SplayTree() {
        tot = nd;
        rt = nullptr;
        no_pre.val = -2147483647;
        no_nxt.val = 2147483647;
    }

    void insert(int x) {
        if (!rt) { 
            rt = ++tot;
            rt->val = x;
            rt->cnt++;
            rt->sz++;
            return;
        }
        Node *now = rt, *fa = nullptr;
        while (now) {
            if (now->val == x) { 
                now->cnt++;
                now->upd();
                fa->upd();
                splay(now);
                return;
            }
            fa = now;
            now = now->ch[x > now->val]; 
        }
        now = ++tot;
        now->val = x;
        now->cnt++;
        now->upd();
        now->fa = fa;
        fa->ch[x > fa->val] = now;
        fa->upd();
        splay(now);
    }

    int get(int k) { 
        Node *now = rt;
        while (now) {
            if (now->ch[0] && k <= now->ch[0]->sz) 
                now = now->ch[0];
            else {
                k -= now->cnt;
                if (now->ch[0])
                    k -= now-
                if (k <= 0)
                    return 
                now = now->ch[1]; 
            }
        }
        return -1;
    }

    Node *pre() {
        Node *now = rt->ch[0];
        if (!now)
            return &no_pre;
        while (now->ch[1])
            now = now->ch[1];
        splay(now);
        return now;
    }
    Node *nxt() {
        Node *now = rt->ch[1];
        if (!now)
            return &no_nxt;
        while (now->ch[0])
            now = now->ch[0];
        splay(now);
        return now;
    }
    void del(int x) {
        if (!exist(x))
            return;
        if (rt->cnt > 1) {
            rt->cnt--;
            rt->sz--;
            return;
        }
        if (!rt->ch[0] && !rt->ch[1]) {
            rt->clear();
            rt = nullptr;
            return;
        }
        if (!rt->ch[0]) {
            Node *_rt = rt;
            rt = rt->ch[1];
            rt->fa = nullptr;
            _rt->clear();
            return;
        }
        if (!rt->ch[1]) {
            Node *_rt = rt; 
            rt = rt->ch[0];
            rt->fa = nullptr;
            _rt->clear();
            return;
        }
        Node *_rt = rt; 
        Node *left = pre();
        _rt->ch[1]->fa = left;
        left->ch[1] = _rt->ch[1];
        _rt->clear();
        rt->upd();
    }
    int rank(int x) {
        insert(x);
        return del(x),(rt->ch[0] ? rt->ch[0]->sz : 0) + 1;
    }

} tree;
int main() {
    int n, opt, x;
    scanf("%d", &n);
    while (n--) {
        scanf("%d%d", &opt, &x);
        switch (opt) {
        case 1:
            tree.insert(x);
            break;
        case 2:
            tree.del(x);
            break;
        case 3:
            printf("%d\n", tree.rank(x));
            break;
        case 4:
            printf("%d\n", tree.get(x));
            break;
        case 5:
            tree.insert(x);
            printf("%d\n", tree.pre()->val);
            tree.del(x);
            break;
        case 6:
            tree.insert(x);
            printf("%d\n", tree.nxt()->val);
            tree.del(x);
            break;
        }
    }
    system("pause");
    return 0;
}

（这份代码是经过VSCode格式化的）

（其实节点数组和tot完全没必要开，直接new node即可）

没错我就是OI面向对象人

\(\mathfrak{To Be Continued}\)

本栏目推荐文章
• splay
• splay学习笔记
• Splay 伸展树扩展应用
• Splay/LCT 学习笔记
• splay + 垃圾回收 知识点与例题的简要讲解
• Splay 学习笔记
• 【数据结构】Splay 树
• 【学习笔记】Splay
• splay
• Splay

Splay1 Splaysplay1 splay1 splay splay splay2 笔记splay 区间splay 模板splay splay lct ett 笔记splay lct splay2 splay