[SDOI2010] 代码拍卖会 题解
题目描述
一个 \(n,n\le10^{18}\) 位数,仅由 \(1\sim9\) 组成,后一位数字一定大于等于前一位数字。
求这些数中可以被 \(m,m\le500\) 整除的有多少,对 \(999911659\) 取模。
解析
这个数一定形如 \(112334455677788999\) 可以把它拆成
最多有 \(9\) 个 \(11\cdots11\) 组成。
现在问题转换成有 \(10^{18}\) 个物品,价值是 \(11\dots111\) 取模 \(m\) ,选择 \(\le9\) 个求和使得可以整除 \(m\) ,求方案数。
我们可以有一种背包计数的 dp 想法,但看起来 \(10^{18}\) 还是不太行。
我们把每个物品按照对 \(m\) 去模得到的结果分类。
然后记录 \(g[i]\) 表示价值为 \(i\) 的有 \(g[i]\) 种物品。
循环节的计算
那么怎么计算 \(g[]\) 数组呢?
普及组知识?
定义 \(s_i\) 表示 \(i\) 个 \(1\) 连起来形成的数, \(f_i\) 为它在 \(\mod p\) 意义下的值。
如 \(s_5=11111\)
\(f_3=1\mod 5\)
则显然有 \(f_i=(10\times f_{i-1}+1)\%p\)
显然这柿子在 \(2p\) 次迭代内必然会出现循环。
可以把 \(f_i\) 分成三段:
-
未进入循环段
-
循环段
-
不完整循环段
暴力统计 未进入和不完整 的,用循环节搞定循环的就好了。
计数
我们不关心这个物品具体是什么,我们只需要保证物品求和去模之后为 \(0\) 就可以了。
假如 \(m = 19\) 我们只需要:
7 个模数为 1 ,2 个模数为 6,或者 3 个模数为5,4 个模数为 1,\(\cdots\)
这一类的情况都是我们想要的。
总的来说,我们要物品总数 \(\le9\) ,价值和整除 \(m\) 。
我们设 \(f[i][j][s]\) 表示用了价值从 \(1\sim i\) 的物品 ,现在总共放了 \(j\) 个物品,总模数为 \(s\) 的方案数。
答案很显然是:
转移也很简单了。
枚举当前价格为 \(i\) 的物品你会选 \(k\) 个。
转移的最后一维减法是在模意义下的。
最后一个组合数代表着 从 \(g[i]\) 中无序(组合)可重复的选择 \(d\) 个数。
为什么是这个,考虑插板法。
组合数
从 \(m\) 个数 \(a_1,a_2,\cdots,a_m\) 中选 \(k\) 个数,我们令 \(a_i\) 选了 \(t_i\) 次。
相当于解方程 \(t_1 + t_2 + \cdots+t_m=n\) 。
我们把所有的 \(t\) 统一先加上 1,保证没有 0。
现在有 \(m + t\) 个点,我们用 \(m - 1\) 隔板在中间去插,首尾默认有两个隔板,会得到 m 个区间。每个区间就代表着 \(t_1\) 的取值。
所以 \(m-1\) 个隔板有 \(m + t - 1\) 种位置可以插入。
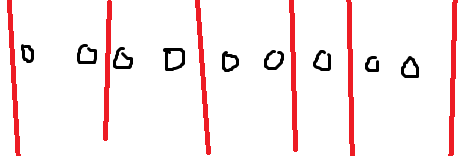
上图代表着从 5 个数中选 4 个的其中一种方案。
温馨提示
因为猪猪不可以选0,所以第一个一定是 \(\underset{n个1}{111\cdots111}\)。那我们只需要找 \(8\) 个,并且最后取答案的模数 + \(\underset{n个1}{111\cdots111}\) = 0。
我代码中的因为模数 \(0\sim{m-1}\) ,初始值就需要设在 \(f[-1][0][0]\) 中,不合法,我就把第一位全部往后移动了一位。
代码
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod = 999911659;
ll n,g[510],f[510][10][510];
int p,d,jl;
vector<int> v[510];
ll qpow(ll x,int k){
ll ans = 1;
while(k){
if(k & 1) ans = ans * x % mod;
x = x * x % mod;
k >>= 1;
}
return ans;
}
ll C(ll n ,ll m){
if(m < 0) return 0;
ll fz = 1 ,fm = 1;
for(ll i = 1; i <= m; ++i){
fz = fz * (n - i + 1) % mod;
fm = fm * i % mod;
}
return fz * qpow(fm ,mod - 2) % mod;
}
void pre(){
int now = 0;
for(int i = 1; i <= 2 * p; ++i){
now = (now * 10 + 1) % p;
v[now].push_back(i);
}
for(int i = 0; i < 500; ++i){
g[i] = 0;
if(v[i].size() == 0 || v[i][0] > n) continue;
if(v[i].size() == 1){
g[i] = v[i].size();
continue;
}
d = v[i][1] - v[i][0];
g[i] = (((n - v[i][0]) / d) + 1 ) % mod;
if((n - v[i][0]) % d == 0){
jl = i;
}
}
}
void op(){
for(int i = 0; i <= p ; ++i) f[i][0][0] = 1;
for(int i = 1; i <= p; ++i){
for(int j = 1; j <= 8; ++j){
for(int k = 0; k <= 1ll * j; ++k){
ll mul = C(g[i - 1] + k - 1,k);
if(k > 0 && g[i - 1] == 0) break;
for(int s = 0; s < p; ++s){//这里换一下dp顺序先枚举 k 在枚举 d 不然算组合数要超时
f[i][j][s] += mul * f[i - 1][j - k][(s - k * (i - 1) % p + p) % p] % mod;
f[i][j][s] %= mod;
}
}
}
}
}
void output(){
ll ans = 0;
for(int i = 0; i <= 8; ++i){
ans = (ans + f[p][i][(p - jl) % p]) % mod;
}
cout<<ans;
}
int main(){
cin>>n>>p;
pre();
op();
output();
return 0;
}