例题一 种植玉米
题目大意
农夫有一个被划分成M行N列的农田。
每个格子的数字如果是1则表示该格子的土地是肥沃的,可以种植玉米;
如果该格子的数字是0则表示该格子不能种植玉米。
但是还有一个条件:不能出现相邻的两个格子都种植玉米的情况。
问有多少种不同的种植方式。
做法
对于1≤M≤12且1≤N≤12
先简化问题,把问题拆分成几个简单的问题:
一、只有1行,且所有格子都可以种玉米。
二、只有1行,有些格子不能种玉米。
三、多行多列,有些格子不能种玉米。
下面具体分析这三种情况。
一、只有1行,且所有格子都可以种玉米。
例如1行3列,每个格子都可以种玉米或者不种玉米,有2^3=8种状态。
但是相邻的两个格子不能同时种植玉米,所以要排除这些状态。
可以对这8种状态之中的每一个状态,都用一个for循环来判断是否存在相邻的两个格子都种植了玉米。
bool ok[1<<maxN]; //保存状态i是否合法。
void check(int n) //一行n列
{
for(int i=0; i<(1<<n); i++)
{
//检查状态i中,第k个格子和第k+1个格子是否同时种植了玉米
ok[i] = true; //先默认状态i是合法的,不存在相邻的两个格子都种植了玉米
for(int k=1; k<n; k++) //第k个格子和第k+1个格子是否同时种植了玉米
{
int bit1 = 1<<(k-1), bit2 = (1<<k);
if( (i&bit1) && (1<<bit2) ){ //状态i的第k个格子和第k+1个格子都种植了玉米
ok[i] = false;
break;
}
}
}
}
调用一下check(3),就可以计算出一行三列的每个种植状态是否合法。
同理,调用一下check(4),就可以计算一行四列的每个种植状态是否合法。
调用一下check(n),就可以计算一行n列的每个种植状态是否合法。
还有另外一种简单的判断方法:
for(int i=0;i<(1<<m);i++)
if(!(i&(i>>1))) ok[i]=true;
二、只有1行,有些格子不能种玉米
例如1行5列的例子。
m=1, n=5, 读入的数据是: 1 0 1 1 1 , 即第2个格子不能种玉米,其他格子可以种玉米。
有多少种合法的种植方案?
我们把读入的数据看成是低位在左边,高位在右边的二进制数: 10111,对应的十进制是:29。
记这个值为d, 即d=29。求d的代码如何如下:
int d = 0, p=1;
for(int i = 1; i <= n; i++)
{
int x;
cin>>x;
d += p * x;
p *= 2;
}
下面计算这个样例的每个种植状态是否合法。这和上面的第一种情况的判断非常类似。
先调用一下check(5), 然后计算出一行五列的每个种植状态是否合法。
check(5); //先算出各种状态是否存在相邻的两个格子同时种植玉米。
int ans = 0; //总共有多少种合法的种植方案。
for(int i=0; i<(1<<5); i++) //枚举每种可能的种植状态i,检查是否合法
{
//如果状态i不存在相邻的两个格子同时种植玉米,而且不在0的格子种植玉米,则这种种植状态合法
if( ok[i] && ( (i|d)==d) ) ans++;
}
三、有3行,有些格子不能种玉米。
例如m=3, n = 5,读入:
3 5
1 1 0 1 1
1 0 1 1 1
0 1 1 1 1
读入数据时,把读入的数据看成是低位在左边,高位在右边的二进制数。
用d[1]保存第一行输入数据对应的十进制数,d[1] = 27。
用d[2]保存第二行输入数据对应的十进制数,d[2] = 29。
用d[3]保存第三行输入数据对应的十进制数,d[2] = 30。
接下来考虑用搜索的思路。
枚举第一行的种植状态为s1, 接着搜索到第2行,发现第1行的种植状态会影响到第2行的种植,
因此在向下递归时,要记录上一行的种植状态。考虑如下的搜索框架:

long long dfs(int row, int status)
{
if( row > m) return 1 ; //递归结束条件,如果超过最后一行了,返回1。思考:为什么不是返回0
for(int s=0; s<(1<<n); s++) //枚举第row行的种植状态是十进制数s, 检查s是否可行。
{
if( ok[s] && (s|d[row])== d[row] && (s&status)==0 )
f[row][status] += dfs(row+1, s);
}
return f[row][status];
}
以上就是递归搜索的大致框架。
但是直接搜索肯定会超时的,可以考虑改成记忆化搜索,搜索过的状态不再搜索。
即f[row][status]这样的状态只搜索一次。
bool vis[maxM][1<<maxN]; //记录某个状态是否搜索过。
long long dfs(int row, int status)
{
if(vis[row][status]) return f[row][status]; //如果这种状态搜索过,直接返回值。
vis[row][status] = true; //先设置成搜索过,再往下搜索。
if( row > m) return 1 ; //递归结束条件,如果超过最后一行了,返回1。思考:为什么不是返回0
for(int s=0; s<(1<<n); s++) //枚举第row行的种植状态是十进制数s, 检查s是否可行。
{
if( ok[s] && (s|d[row])== d[row] && (s&status)==0 )
f[row][status] += dfs(row+1, s);
}
return f[row][status];
}
下面分析一下这种算法的时间复杂度:
1、首先状态数是 f[maxM][1<<maxN], 共m * 2^n个。
2、对于每一个这样的状态,我们要枚举当前行的种植状态s。s共有2^n个。
3、所以上面的时间复杂度是: m * 2^n * 2^n = m * 4^n。
当m=12, n=12时,可以通过。
对于1≤M≤15且1≤N≤15
方法一
前面一题的算法慢的原因是每次要枚举某一行的种植状态,每次枚举都是2^n复杂度。
下面介绍另一种递归的解法。
用0表示格子不种植玉米,1表示种植了玉米。如图所示,灰色区域的格子已经全部考虑完毕,现在还剩下蓝色区域的格子需要考虑。
我们考虑种植玉米的方向是从上往下、从左往右。
那么,第r行第c列格子是否能够种植玉米,主要取决于它左邻格子和上邻格子的种植状态。有如下4种情况:
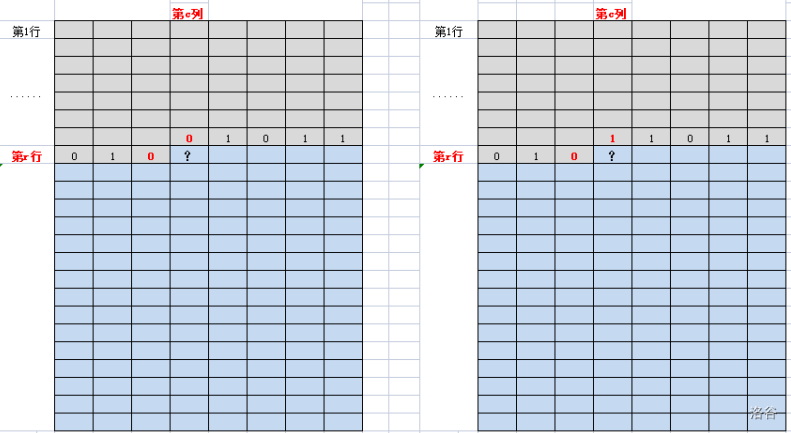
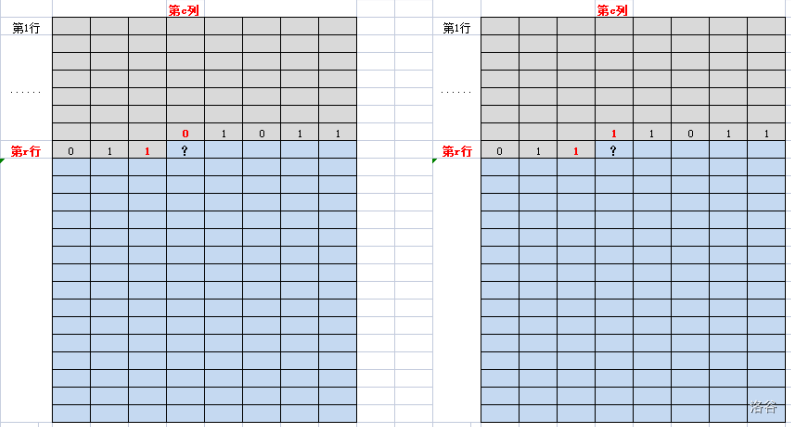
考虑第一种情况的状态转移:
第r行的前c-1个格子的种植状态是010,第r-1行的第c列至最后一列的种植状态是01011, 在此前提下,蓝色区域格子有多少种合法的种植状态?
记为f[r][c][s], 其中s=01001011,即f[r][c][01001011]。
分情况讨论第r行第c列的格子是否种植玉米:
(一)若第r行第c列的格子是障碍物,不能种植玉米,那么f[r][c][s] = f[r][c+1][01001011]。
(二)若第r行第c列的格子不是障碍物,可以分两种情况:
1、不在这个格子种植玉米,那么子问题是: f[r][c+1][01001011]。
2、在这个格子种植玉米,那么子问题是: f[r][c+1][01011011]。因为第r行第c列格子的上邻和左邻都没有种植玉米。
根据加法原理,f[r][c][s] = f[r][c+1][01001011] + f[r][c+1][01011011]。
考虑第二种情况的状态转移:
第r行的前c-1个格子的种植状态是010,第r-1行的第c列至最后一列的种植状态是11011, 在此前提下,蓝色区域格子有多少种合法的种植状态?
记为f[r][c][s], 其中s=01011011,即f[r][c][01011011]。
分情况讨论第r行第c列的格子是否种植玉米:
(一)若第r行第c列的格子是障碍物,不能种植玉米,那么f[r][c][01011011] = f[r][c+1][01001011]。
(二)若第r行第c列的格子不是障碍物,因为第r-1行第c列格子已经种植了玉米,所以第r行第c列格子肯定不能种植玉米,故f[r][c][01011011] = f[r][c+1][01001011] 。
总结上述四种情况,只要一种情况是可以在第r行第c列格子种植玉米:第r行第c列格子的左邻和上邻都没有种植玉米,且第r行第c列格子读入数据的值是1。
可以用记忆化搜索去实现,框架如下:
bool vis[maxM][maxN][maxS];
long long f[maxM][maxN][maxS];
long long dfs(int r, int c, int s) {
if(r > m) return 1; //递归结束边界
if(c > n) return dfs(r+1,1,s); //超过最右边的列,则转移到下一行
if( vis[r][c][s]) return f[r][c][s]; //如果已经计算过,就直接返回值
vis[r][c][s] = true; //先设置为已经计算过
......
1、分情况来决策第r行第c列格子是否种植玉米,然后递归相应的子问题。
2、根据子问题的解,求出f[r][c][s],并返回该值。
}
状态总数:O(m*n*2n),状态转移:O(1),总时间复杂度:O(m*n*2n)。
本算法相比枚举一行的种植状态要快,原因是:从上往下、从左往右,一个一个格子的做决策。
方法二
记d[i][j]保存读入数据时,第i行第j列格子是否可以种植玉米,0表示该格子被禁止种植玉米,1则表示不禁止。约定用(r,c)表示第r行第c列格子。
换一种方式描述状压DP的状态,
先观察下图:

灰色区域的格子已经全部考虑完毕,现在还剩下蓝色区域的格子需要考虑。
令s = 01001011,这里的0和1不是描述该格子的种植状态,而是描述该格子的种植状态对正下方格子的影响。
s的前三位010表示第r行的前3个格子对第r+1行的前3个格子的影响;
s的01011表示第r-1行最右边5个格子对第r行最右边5个格子的影响,
则:
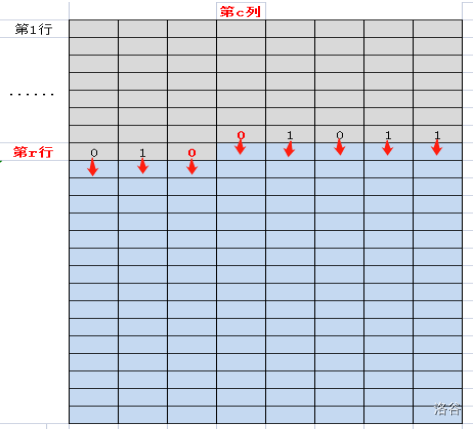
我们可以约定,s的某位是0则表示该格子的种植状态会限制它正下方格子种植玉米,1则表示该格子的种植状态不会限制它正下方格子种植玉米。
那么结合上图的s = 01001011 ,则会有这样的限制效果:
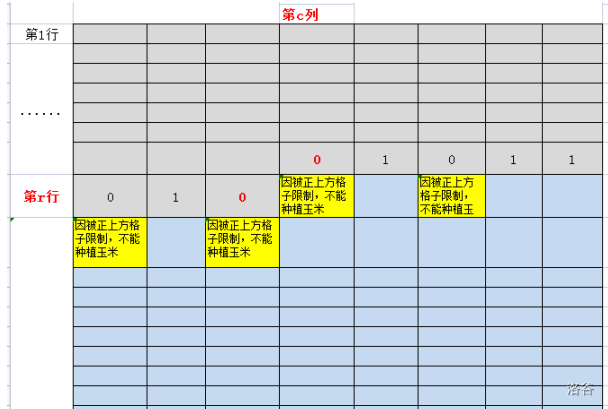
定义好了状态的意义之后,我们考虑种植玉米的方向是从上往下、从左往右,逐个格子考虑。
一、有三种情况会使得格子(r,c)不能种植玉米:
1、读入数据的d[r][c] 等于0
2、上邻格子(r-1,c)种植了玉米,即二进制状态s的第c位是0。
3、左邻格子(r,c-1)种植了玉米,这种情况应该体现出(r,c)格子禁止种植玉米?我们可以强行设置s的第c位为0即可达到目的。所以,当格子(r,c-1)种植了玉米之后,应该强行设置s的第c位为0。
二、格子(r,c)能够种植玉米必须同时满足:
1、读入数据的d[r][c] 等于1
2、二进制状态s的第c位是1。
综合上述两种描述,我们可以用记忆化搜索去实现,灰色区域格子已经考虑完毕,二进制限制状态为s,
在此状态下,蓝色区域格子有多少种合法的种植状态?记为f[r][c][s]。
现在只需要决策格子(r,c)是否种植玉米就可以递归子问题了。
一、若d[r][c]=0,则f[r][c][s] = dfs(r,c+1,setOne(s,c))。其中setOne(s,c)意思是把s的第c位设置成1,因为格子(r,c)不种植玉米,所以不应该限制(r+1,c)格子种植玉米。
二、若s的第c位为0, 则f[r][c][s] = dfs(r,c+1,setOne(s,c))。其中setOne(s,c)意思是把s的第c位设置成1,因为格子(r,c)不种植玉米,所以不应该限制(r+1,c)格子种植玉米。
三、若d[r][c]=1且s的第c位为1,那么格子(r,c)可种玉米也可不种玉米:
1. 若(r,c)决定不种玉米,令x = dfs(r,c+1,setOne(s,c))。其中setOne(s,c)意思是把s的第c位设置成1,因为格子(r,c)不种植玉米,所以不应该限制(r+1,c)格子种植玉米。
2. 若(r,c)决定种植玉米,令y = dfs(r,c+1,setZero(s,c),若c<n再setZero(s,c+1),则(r,c)种植了玉米后,(r,c+1)禁止种植玉米,(r+1,c)也禁止种植玉米。
3、根据加法原理,f[r][c][s] = (x+y) % mod
四、递归边界
1、若r>m,则return 1;
2、若c>n,则return f[r][c][s] = dfs(r+1,c,s)。
状态总数:O(m*n*2n),状态转移:O(1),总时间复杂度:O(m*n*2n)。
代码(采用方法二)
#include<bits/stdc++.h>
using namespace std;
const int p=1e8,maxn=15;
int m,n,f[maxn+5][maxn+5][(1<<maxn)+10],a[maxn+5][maxn+5];
int dfs(int r,int c,int num){
if(r>m)return 1;
if(c>n)return dfs(r+1,1,num);
if(~f[r][c][num])return f[r][c][num];
f[r][c][num]=0;
int x=dfs(r,c+1,(num|(1<<(c-1)))^(1<<(c-1)));
int y=0;
if(a[r][c]&& ( c==1 || !((1<<(c-2))&num) )&&!((1<<(c-1)) &num))y=dfs(r,c+1,(num|(1<<(c-1))));
return f[r][c][num]=(x+y)%p;
}
int main(){
memset(f,-1,sizeof f);
cin>>m>>n;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];
cout<<dfs(1,1,0);
return 0;
}
例题二 铺地砖
题目大意

做法1(1 < = h,w < = 12)
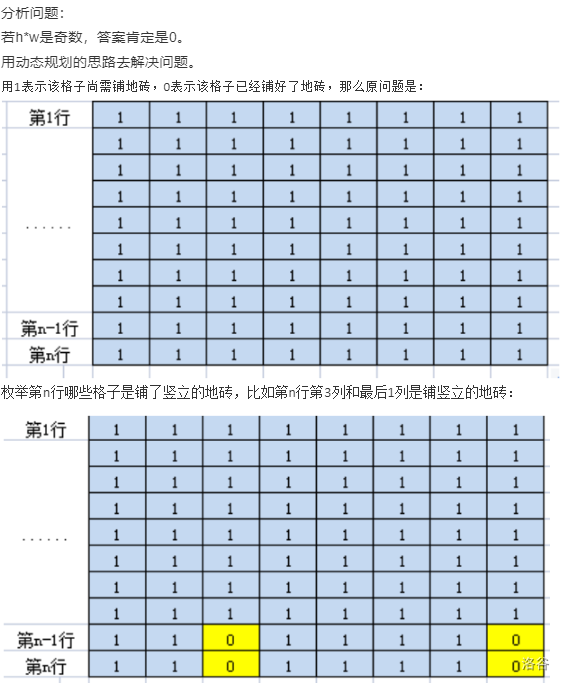
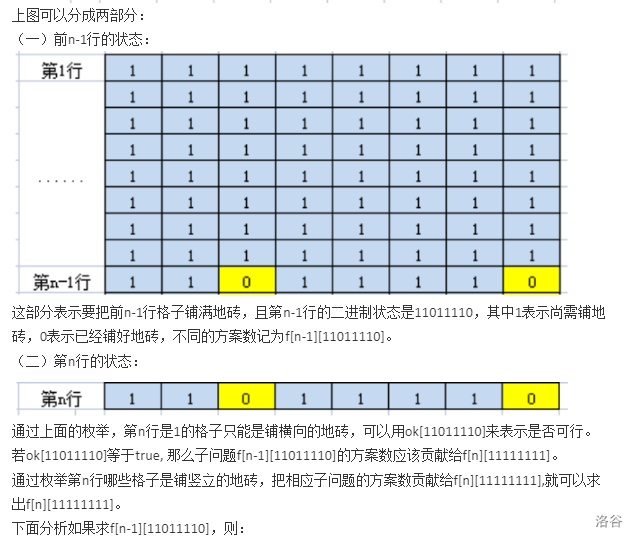
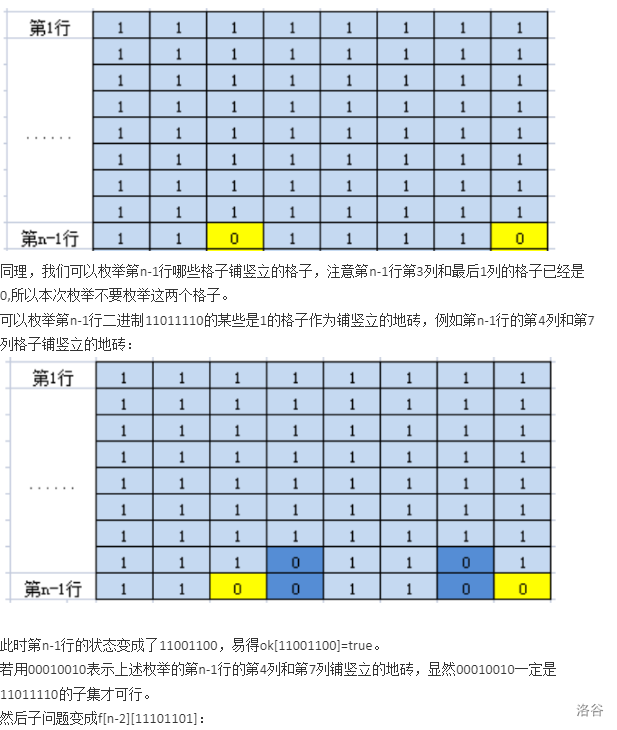
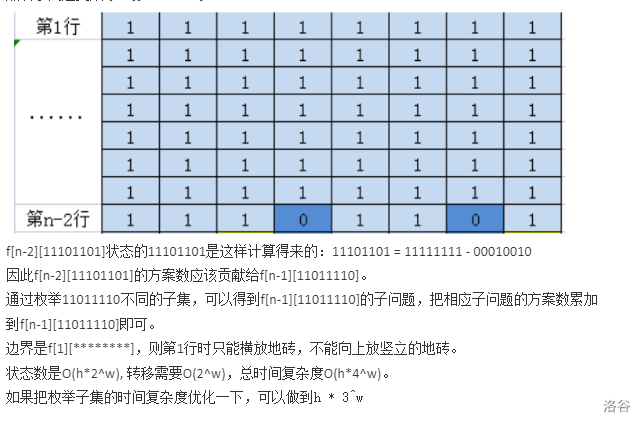
代码1
#include<bits/stdc++.h>
using namespace std;
const int maxn=16,p=1e9+7;
int w,h,ok[(1<<maxn)+10],f[maxn+5][(1<<maxn)+10];
void init(){
ok[0]=true;
for(int i=1;i<(1<<w);i++){
int cnt=0;
bool flag=true;
for(int j=1;j<=w;j++){
if(i&(1<<(j-1)))
cnt++;
else{
if(cnt%2==1){
flag=false;
break;
}
else cnt=0;
}
}
if(cnt%2==1)flag=false;
ok[i]=flag;
}
return ;
}
int main(){
cin>>h>>w;
if(h*w%2==1){
cout<<0<<endl;
return 0;
}
f[1][0]=1;
int tot=(1<<w)-1;
init();
for(int i=1;i<=tot;i++)
if(ok[i])f[1][i]=1;
for(int i=2;i<=h;i++){
f[i][0]=f[i-1][tot];
for(int j=1;j<=tot;j++){
if(ok[j])f[i][j]=f[i-1][tot];
for(int k=j;k!=0;k=(k-1)&j)
if(ok[j^k])f[i][j]=(f[i][j]+f[i-1][tot^k])%p;
}
}
cout<<f[h][tot];
return 0;
}
做法二(1 < = h,w < = 16)
约定用(r,c)表示第r行第c列格子。先观察下图:

灰色区域的格子已经全部铺完地砖,现在还剩下蓝色区域的格子需要铺地砖。
令s = 01001011,这里的0和1是描述该格子的铺砖状态对正下方格子的影响。
s的前三位010表示第r行的前3个格子对第r+1行的前3个格子的影响;
s的01011表示第r-1行最右边5个格子对第r行最右边5个格子的影响。则:
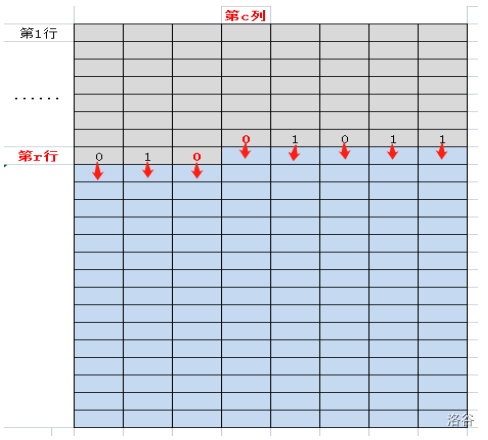
我们可以约定,若s的某位是0则表示该格子铺的地砖不会延申到它正下方格子,1则表示该格子铺了垂直的地砖,它正下方格子会被这地砖覆盖。
那么结合上图的s = 01001011 ,则会有这样的限制效果:
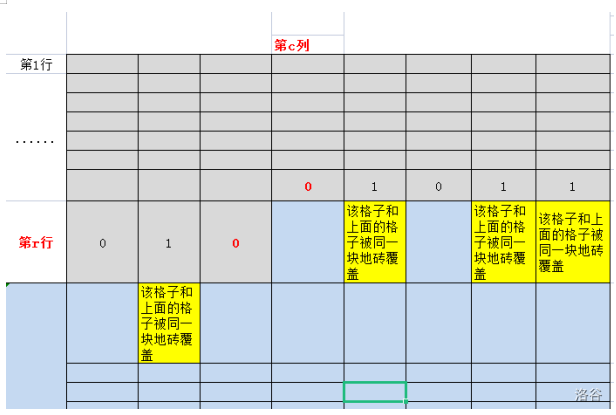
定义好了状态的意义之后,我们考虑铺地砖的方向是从上往下、从左往右,逐个格子考虑。
一、有两种情况会使得格子(r,c)不用铺地砖:
1、上邻格子(r-1,c)铺了一块垂直的地砖且延申到(r,c),即二进制状态s的第c位是1。
2、左邻格子(r,c-1)铺了一块水平的地砖且延申到(r,c),这种情况应该如何体现出(r,c)格子要禁止再铺地砖?
我们可以强行设置s的第c位为1即可达到目的。所以,当决定在格子(r,c-1)铺一块水平的地砖且延申到(r,c)的时候,应该强行设置s的第c位为1。
二、若s的第c位是0,则表示(r,c)必须要铺地砖:
1、在(r,c)铺一块垂直向下的地砖,记合法的方案数为x。此时应该把s的第c位设置成为1,因为它会使得(r+1,c)格子不用再铺地砖, 容易得到x = dfs(r,c+1,setOne(s,c))。
2、在(r,c)铺一块水平向右的地砖,记合法的方案数为y。此时应该把s的第c位设置成为0,同时把s的第c+1位设置成为1,这样(r,c+1)格子就不用再铺地砖, 容易得到y = dfs(r,c+1,setOne(s,c+1))。
综合上述两种描述,我们可以用记忆化搜索去实现,灰色区域格子已经铺地砖完毕,二进制限制状态为s,在此状态下,蓝色区域格子有多少种合法的铺砖状态?
记为f[r][c][s]。现在只需要决策格子(r,c)是否需要铺地砖,以及铺水平地砖还是垂直地砖,就可以递归子问题了。
一、若s的第c位为1,f[r][c][s] = dfs(r,c+1,setZero(r,c))。
二、若s的第c位为0, 则需要决策(r,c)是铺垂下向下地砖或者铺水平向右地砖:
1、若(r,c)决定铺垂直向下地砖,令x = dfs(r,c+1,setOne(s,c))。其中setOne(s,c)意思是把s的第c位设置成1,因为格子(r+1,c)和(r,c)是同一块地砖,所以(r+1,c)不用再铺地砖。前提是:r<h。
2. 若(r,c)决定铺水平向右地砖,要同时满足两个条件:
(1) c < w。
(2) s的第c+1位必须是0,则(r,c+1)并没有和(r-1,c+1)共用一块垂直的地砖。令 y = dfs(r,c+1,setOne(s,c+1)),因为(r,c)铺了水平向右的地砖后,(r,c+1)不用再铺地砖。
3、根据加法原理,f[r][c][s] = (x+y) % mod
四、递归边界
1、若r > h,则return 1;
2、若c > w,则return f[r][c][s] = dfs(r+1,c,s)。
代码二
#include<bits/stdc++.h>
using namespace std;
const int maxn=16,p=1e9+7;
int f[maxn+5][maxn+5][(1<<maxn)+10],h,w,tot=0;
int set0(int num,int pos){
return ((num|(1<<(pos-1)))^(1<<(pos-1)));
}
int set1(int num,int pos){
return (num|(1<<(pos-1)));
}
int dfs(int r,int c,int num){
if(r>h)return 1;
if(c>w)return dfs(r+1,1,num);
if(~f[r][c][num])return f[r][c][num];
f[r][c][num]=0;
int x=0,y=0;
if(num&(1<<(c-1)))return f[r][c][num]=dfs(r,c+1,set0(num,c));
if(c<w&&(!(num&(1<<c))))
x=dfs(r,c+1,set0(set1(num,c+1),c));
if(r<h)
y=dfs(r,c+1,set1(num,c));
return f[r][c][num]=(x+y)%p;
}
int main(){
cin>>h>>w;
memset(f,-1,sizeof f);
if(h*w%2==1){
cout<<0;
return 0;
}
tot=(1<<w)-1;
cout<<dfs(1,1,0);
return 0;
}
例题三 一笔画
题目大意
由于小毛同学智商不高,理解不了真正的一笔画问题,于是他就开始研究一种变形的一笔画问题。
给出 n 行 m 列的点阵,每个点是一个字符: “.” 或 “#” ,其中“#”表示该点是障碍物。
现在小毛的问题是: 他最少要画多少笔才能把点阵里所有的“.”都覆盖完毕(被小毛画到的点就会被覆盖)。
小毛的笔有点奇怪:小毛每次只能在某一行或某一列画,小毛当然想一笔就把某一行或某一列画完,
但很遗憾,在任何时候都不允许小毛画的那一段点阵含有障碍物。
还有一点更奇怪: 已经被画过的点,不能重复被画。
0 < n, m <=15
做法
记f[i][j][k]为i行j列当前状态为k,1为横,0为列
其余显然
时间复杂度: h * w * 2^w
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=15;
int n,m,f[maxn+10][maxn+10][(1<<maxn)+10];
bool a[maxn+10][maxn+10]={false};
char C;
int set0(int num,int pos){
return ((num|(1<<(pos-1)))^(1<<pos-1));
}
int set1(int num,int pos){
return (num|(1<<(pos-1)));
}
bool IN(int num,int pos){
return num&(1<<(pos-1));
}
int dfs(int r,int c,int num){
if(r>n)return 0;
if(c>m)return dfs(r+1,1,num);
if(~f[r][c][num])return f[r][c][num];
f[r][c][num]=1e9+7;
if(a[r][c])
return f[r][c][num]=dfs(r,c+1,set0(num,c));
int x=1e9+7,y=1e9+7;
if(IN(num,c))x=dfs(r,c+1,set1(num,c));
else x=dfs(r,c+1,set1(num,c))+1;
if(c!=1&&!a[r][c-1]&&!IN(num,c-1))y=dfs(r,c+1,set0(num,c));
else y=dfs(r,c+1,set0(num,c))+1;
return f[r][c][num]=min(x,y);
}
int main(){
cin>>n>>m;
memset(f,-1,sizeof f);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>C;
if(C=='#')a[i][j]=1;
}
}
cout<<dfs(1,1,0);
return 0;
}
例题四 恐怖电影
题目大意
John 有N部恐怖片子,编号0 至 N-1。第i部恐怖片的播放总长度是Length[i]分钟。
现在John 很累了, 所以他可能在看某部电影过程中睡着了。
唯一能让他一直保持不睡着的条件是:他受到的惊吓程度Level始终不低于某个值。
一开始 ,John 没看任何恐怖片之前的Level是定值74。
他的Level随着时间的流逝而递减,每过一分钟就减少1。
例如过了6秒后,那么Level值就减少0.1。
一旦Level值小于 -0.5, 那么 John 就睡着了。
每个恐怖片只有一个恐怖镜头,一旦John 看到了这个恐怖镜头,他的Level值马上增加 47。
第i个恐怖片的恐怖镜头在该片子的第scary[i] 分钟出现。
现在John想看完尽量多的恐怖片,他让你帮它安排恐怖片的编号的排列,
就是说,你要决定一个0至N-1的排列,按照这个顺序,John就可以在睡着前能看完尽量多的恐怖片。
如果有多种方案可以看完相同多的恐怖片,输出字典序最小的序列。
注意:一个恐怖片只有被John从头看到尾,才算看完, 一旦John在看这个恐怖片过程中睡着了,
那么他就没办法看完这部恐怖片,剩下还没看的哪些恐怖片也无法再看到了。
注意:电影是连续播放的,即一个电影完了后,瞬间就播放下一个电影。
做法
先不管字典序,看一下他能看那些电影,然后记录当前状态后他能看几部电影,挑多的,相同则选字典序靠前的
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=20;
bool vis[(1<<maxn)+10];
int n,maxx=0,pick[(1<<maxn)+10],f[(1<<maxn)+10],tot;
double a[maxn+10],b[maxn+10];
bool IN(int num,int pos){
return num&(1<<(pos-1));
}
int check(int num){
int ans=0;
while(num){
ans+=num%2;
num/=2;
}
return ans;
}
void chang(int num){
while(num){
cout<<num%2;
num/=2;
}
cout<<"\n";
return ;
}
void dfs(int num,double L){
// chang(num);
if(vis[num])return ;
vis[num]=true;
pick[num]=-1;
f[num]=0;
for(int i=1;i<=n;i++){
if(IN(num,i))continue;
if(L-b[i]<0)continue;
if(L+47-a[i]<0)continue;
int Next=(num^(1<<(i-1)));
dfs(Next,L+47-a[i]);
if(1+f[Next]>f[num]){
f[num]=1+f[Next];
pick[num]=i;
}
}
return ;
}
int main(){
cin>>n;
memset(vis,false,sizeof vis);
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
tot=(1<<n)-1;
dfs(0,74);
int st=0,used=0;
while(pick[st]!=-1){
cout<<pick[st]-1<<" ";
st+=(1<<(pick[st]-1));
}
for(int i=1;i<=n;i++)if(!IN(st,i))cout<<i-1<<" ";
return 0;
}
例题五 送礼物
题目大意
给出一个n行m列的点阵,“.” 表示可通行格子,“#” 表示不可通行格
子,
“K” 表示国王的初始位置,“Q”表示王后的位置,“G”表示该格子有一个礼物。
注意:国王、王后、礼物所在的格子可以认为是可通行格子的。
国王从开始位置出发,国王从当前格子可以走到上、下、左、右四个相邻格子,当然前提是可通行格子。
国王从当前格子走到相邻格子的时间是变化的,这取决于国王手头上收集到的礼物的数量,
假如当前国王手头上有y个礼物,那么他从当前格子移动到相邻格子的所用时间是y+1秒。
一旦国王进入某个有礼物的格子,他可以选择取该格子的礼物,也可以选择不取该格子的礼物。
取礼物这个动作可以认为是瞬间完成的,不需要时间。国王想收集到尽量多的礼物送给王后,
但是他到达王后所在的格子不能超过T秒,王后不想等太长时间。
注意:国王在收集礼物的途中可能多次走到相同的格子。
1 ≤ n, m ≤ 50
做法
先跑一遍floyd,剩下显然
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
struct node{
int x,y;
}K,Q,G[20],q1[2505];
int dirx[]={0,1,0,-1,0};
int diry[]={0,0,1,0,-1};
int n,m,a[55][55],d[20][20],cnt=0,T,f[(1<<18)+10][20],NUM[(1<<18)+10],q2[2505];
bool vis[55][55];
char c;
bool IN(int num,int pos){
return num&(1<<(pos-1));
}
bool check(int x,int y){
return 1<=x&&x<=n&&1<=y&&y<=m&&a[x][y]!=-2&&(!vis[x][y]);
}
bool cmp(node x,node y){
return (x.x==y.x)&&(x.y==y.y);
}
int check(int num){
int ans=0;
while(num){
ans+=num%2;
num/=2;
}
return ans;
}
void bfs(int st){
memset(vis,false,sizeof vis );
int qst=1,qen=0;
q1[++qen]=G[st];
q2[qen]=0;
vis[G[st].x][G[st].y]=true;
while(qst<=qen){
node now=q1[qst];
int tt=q2[qst];
qst++;
if(a[now.x][now.y]>=0){
int tmp=a[now.x][now.y];
d[st][tmp]=tt;
d[tmp][st]=tt;
}
for(int i=1;i<=4;i++){
int nx=now.x+dirx[i];
int ny=now.y+diry[i];
if(!check(nx,ny))continue;
qen++;
q1[qen]={nx,ny};
vis[nx][ny]=true;
q2[qen]=tt+1;
}
}
return ;
}
signed main(){
cin>>n>>m>>T;
cnt=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>c;
if(c=='#')a[i][j]=-2;
if(c=='.')a[i][j]=-1;
if(c=='G')a[i][j]=cnt+1,G[++cnt]={i,j};
if(c=='K')a[i][j]=-3,K={i,j};
if(c=='Q')a[i][j]=-4,Q={i,j};
}
}
a[K.x][K.y]=0;
a[Q.x][Q.y]=cnt+1;
G[0]=K,G[cnt+1]=Q;
for(int i=0;i<=cnt+1;i++){
for(int j=0;j<=cnt+1;j++){
d[i][j]=d[j][i]=1e9+7;
if(i==j)d[i][j]=0;
}
}
for(int i=0;i<=cnt+1;i++){
bfs(i);
}
// for(int i=0;i<=cnt+1;i++){
// for(int j=i+1;j<=cnt+1;j++){
// cout<<i<<" "<<j<<" "<<d[i][j]<<"\n";
// }
// }
memset(f,0x3f,sizeof f);
int tot=(1<<cnt)-1;
for(int i=1;i<=tot;i++)NUM[i]=check(i);
for(int i=1;i<=cnt;i++){
f[(1<<(i-1))][i]=d[0][i];
}
for(int i=1;i<=tot;i++){
for(int j=1;j<=cnt;j++){
if(!IN(i,j))continue;
for(int k=1;k<=cnt;k++){
if(!IN(i,k)||j==k)continue;
f[i][j]=min(f[i^(1<<(j-1))][k]+d[k][j]*(NUM[i]-1+1),f[i][j]);
}
}
}
int maxx=0;
for(int i=1;i<=tot;i++){
for(int j=1;j<=cnt;j++){
if(!IN(i,j))continue;
// cout<<i<<" "<<j<<" "<<f[i][j]+d[j][cnt+1]*(NUM[i]+1)<<endl;
if(f[i][j]+d[j][cnt+1]*(NUM[i]+1)<=T)maxx=max(maxx,NUM[i]);
}
}
cout<<maxx;
return 0;
}
例题六 「九省联考 2018」一双木棋
做法
代码
#include<bits/stdc++.h>
using namespace std;
int n,m,f[(1<<20)+10][3],a[3][15][15];
bool IN(int num,int pos){
return num&(1<<(pos-1));
}
void dfs(int num,bool who){
if(num==((1<<n)-1)*(1<<m)){
f[num][who]=0;
return ;
}
if(~f[num][who])return ;
f[num][who]=-(1e9+7);
int X=n+1,Y=0;
if(num&1)X--;
else Y++;
for(int i=2;i<=(n+m);i++){
if(num&(1<<(i-1)))X--;
else Y++;
if((!IN(num,i))&&IN(num,i-1)){
int Next=num^(1<<(i-1))^(1<<(i-2));
dfs(Next,!who);
f[num][who]=max(f[num][who],-1*f[Next][!who]+a[who][X][Y]);
}
}
return ;
}
int main(){
memset(f,-1,sizeof f);
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[0][i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>a[1][i][j];
dfs((1<<n)-1,0);
cout<<f[(1<<n)-1][0];
return 0;
}
写在最后
1、最大值最好用tot=(1<<n)-1表示
2、尽量使用IN(num,pos)来检查pos位是否为1
3、轮廓线dp用set0,set1
4、不要忘了枚举子集的写法