在过去的几年中，基于深度学习的生成模型越来越受到关注，一方面这是因为该领域产生了一些惊人改进，另一方面受到关注也暗示着该领域进展迅猛。依靠大量数据，精心设计的网络体系结构和智能培训技术，深入的生成模型已经显示出了令人难以置信的能力，可以生成各种高度逼真的各种内容，例如图像，文本和声音。在这些深层的生成模型中，有两个主要的家族脱颖而出，值得特别注意的有：生成对抗网络（GAN）和变分自编码器（VAE）。

从PCA到VAE

在第一部分中，我们将从讨论与降维有关的一些概念开始。特别是，我们将简要回顾主成分分析（PCA）和自动编码器，以显示这两种思想之间的相互关系。

什么是降维

在机器学习中，降维是减少描述某些数据的特征数量的过程。可以通过选择（仅保留一些现有特征）或通过提取（基于旧特征来减少数量的新特征）来进行此简化，并且在许多需要低维数据（数据可视化，数据存储，繁重的计算...）。尽管存在许多不同的降维方法，但是我们可以设置一个与大多数（如果没有的话）方法相匹配的全局框架。

首先，我们称编码器为从“旧特征”表示中产生“新特征”表示（通过选择或提取）的过程，然后将逆过程解码。然后，降维可以解释为数据压缩，其中编码器压缩数据（从初始空间到编码空间，也称为潜在空间），而解码器将其解压缩。当然，根据初始数据分布，潜在空间尺寸和编码器定义，此压缩可能是有损的，这意味着一部分信息在编码过程中丢失，并且在解码时无法恢复。

降维方法的主要目的是在给定系列中找到最佳的编码器/解码器对。换句话说，对于给定的一组可能的编码器和解码器，我们正在寻找在编码时保持信息量最大，因此在解码时具有最小重构误差的对。

主成分分析（PCA）

PCA的想法是构建 $n_e$ 个新的独立特征，这些特征是 $n_d$ 个旧特征的线性组合，以便这些新特征所定义的子空间上的数据投影尽可能接近初始数据（就欧几里得而言）距离）。换句话说，PCA正在寻找初始空间的最佳线性子空间（通过新特征的正交描述），以使通过其在该子空间上的投影近似数据的误差尽可能小。

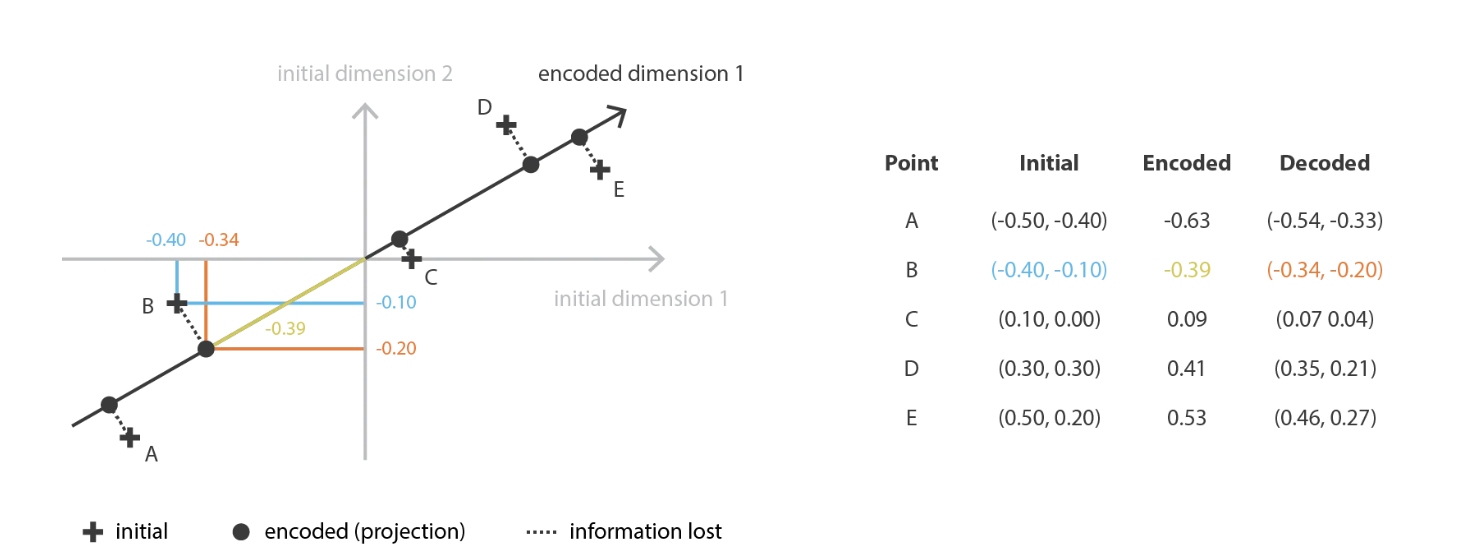
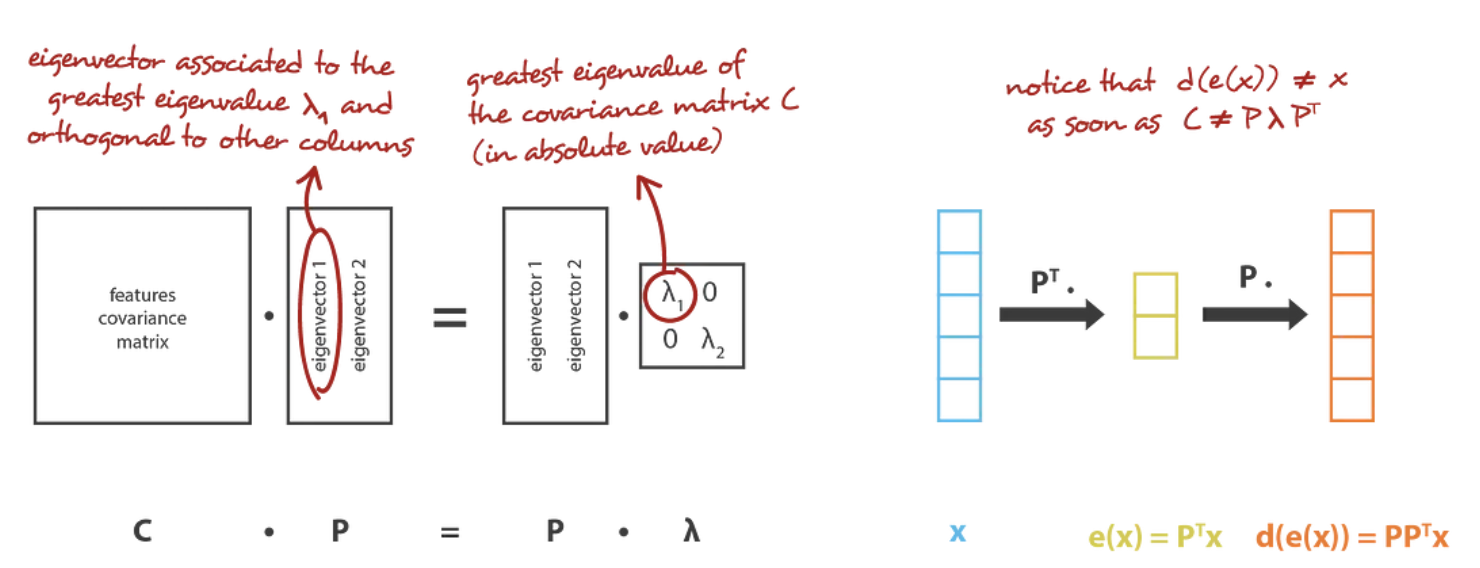
在我们的全局框架中进行转换，我们正在寻找 $n_e$ 族的 $n_d$ 矩阵（线性变换）中的编码器，其行是正交的（特征独立性），以及 $n_d$ 族D的相关解码器（$n_e$ 矩阵）。可以证明，与协方差特征矩阵的 $n_e$ 个最大特征值（在范数上）相对应的unit特征向量是正交的（或可以这样选择），并定义维度 $n_e$ 的最佳子空间以最小的误差将数据投影到近似。因此，可以选择这些 $n_e$ 个特征向量作为我们的新特征，因此，降维问题可以表示为特征值/特征向量问题。此外，还可以示出，在这种情况下，解码器矩阵是编码器矩阵的转置。

Autoencoders

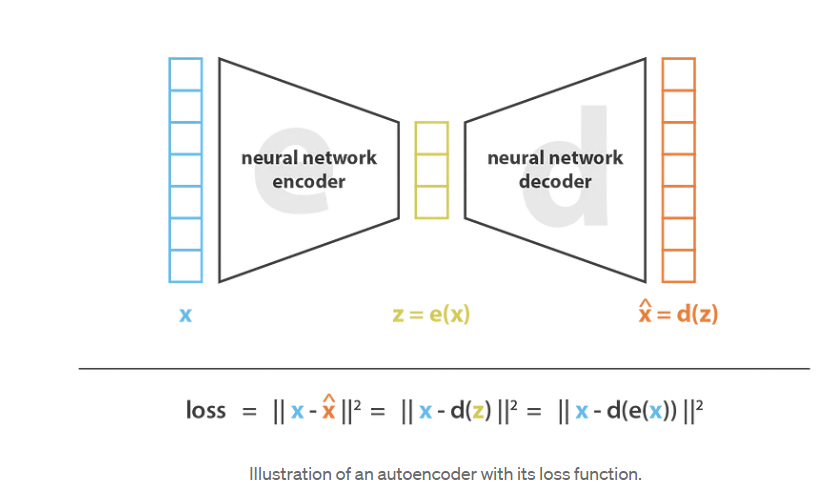
自动编码器的总体思想非常简单，将编码器和解码器设置为神经网络，并使用迭代优化过程学习最佳的编码解码方案。因此，在每次迭代中，我们向自动编码器架构（编码器后跟解码器）提供一些数据，将编码解码输出与初始数据进行比较，并通过架构反向传播误差以更新网络的权重。

因此，直观地说，整个自动编码器架构（编码器+解码器）为数据创建了一个瓶颈（bottleneck），确保只有信息的主要结构化部分可以通过并被重建。看看我们的总体框架，所考虑的编码器系列 E 由编码器网络架构定义，所考虑的解码器系列 D 由解码器网络架构定义，并且通过梯度下降完成最小化重建误差的编码器和解码器的搜索通过这些网络的参数。

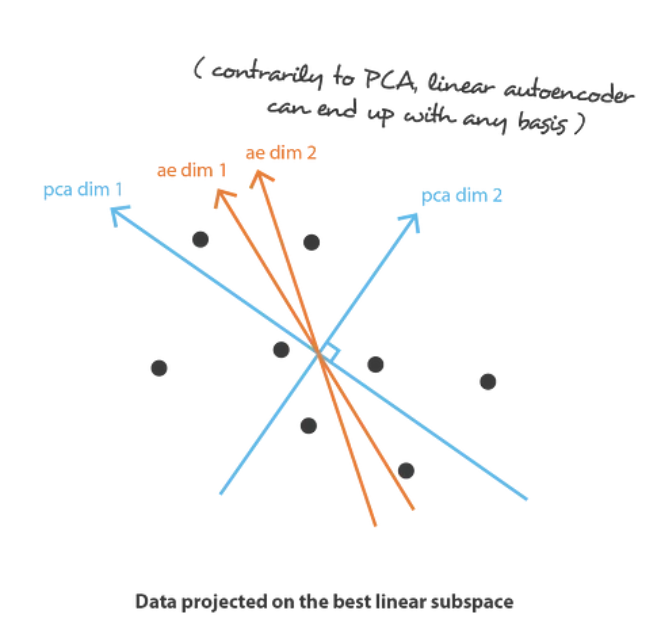
首先假设我们的编码器和解码器架构都只有一层，没有非线性（线性自动编码器）。这样的编码器和解码器是可以表示为矩阵的简单线性变换。在这种情况下，我们可以看到与 PCA 的明显联系，就像 PCA 一样，我们正在寻找最佳的线性子空间来投影数据，同时尽可能减少信息丢失。用 PCA 获得的编码和解码矩阵自然地定义了我们通过梯度下降所满意达到的解决方案之一，但我们应该概述这不是唯一的解决方案。事实上，可以选择多个基(basis)来描述相同的最佳子空间，因此，多个编码器/解码器对可以给出最佳重建误差。此外，对于线性自动编码器，与 PCA 相反，我们最终得到的新特征不必是独立的（神经网络中没有正交性约束）。

现在，我们假设编码器和解码器都是深度且非线性的。在这种情况下，架构越复杂，自动编码器就越能进行高维数降低，同时保持较低的重建损失。直观地说，如果我们的编码器和解码器有足够的自由度，我们可以将任何初始维度减少到 1。

然而，我们应该记住两件事。

在没有重建损失的情况下进行重要的降维通常会带来代价：潜在空间中缺乏可解释和可利用的结构（缺乏规律性）。
很多时候降维的最终目的不仅仅是降低数据的维数，而是降低维数的同时将数据结构信息的主要部分保留在减少的表示中。

Limitation

此时我们想到的一个自然问题是“自动编码器和内容生成之间的联系是什么？”，事实上，一旦自动编码器经过训练，我们就有了编码器和解码器，但仍然没有真正的方法来生成任何新内容。乍一看，我们可能会想，如果潜在空间足够规则（编码器在训练过程中“组织”得很好），我们可以从该潜在空间中随机取出一个点并将其解码以获得新的内容。然后，解码器的行为或多或少类似于生成对抗网络的生成器

但是，正如我们在上一节中讨论的那样，自动编码器的潜在空间的规则性是一个难点，这取决于初始空间中数据的分布，潜在空间的大小和编码器的体系结构。因此，很难（如果不是不可能）先验地确保编码器将以与我们刚刚描述的生成过程兼容的智能方式组织潜空间。

为了说明这一点，让我们考虑之前给出的示例，在该示例中，我们描述了一种强大的编码器和解码器，可以将任何N个初始训练数据放到实轴上（每个数据点都被编码为实数值），并且无需任何解码就可以解码重建损失。在这种情况下，自动编码器的高度自由度使得可以在没有信息损失的情况下进行编码和解码（尽管潜在空间的维数较低）会导致严重的过拟合，这意味着潜在空间的某些点将给出无意义的内容一旦解码。如果自愿选择此一维示例的极端性，我们可以注意到自动编码器潜在空间规则性的问题要比这普遍得多，应特别注意。

稍微想一下就会明白，将数据编码到潜空间后，样本之间不连续，存在很多没有意义的潜向量。这是合理的，因为在自动编码器的训练过程中，的确没有约束潜空间向量之间的关联：无论如何组织潜在空间，自动编码器的训练目标只是以尽可能少的损失进行编码和解码。因此，如果我们没有谨慎地定义编码器和解码器的网络结构，那么很自然的，在训练过程中，网络会利用任何过度拟合的可能性来尽可能地完成其任务……除非我们明确对其进行规范化！

因此，为了能够将自动编码器的解码器用于生成目的，我们必须确保潜在空间足够规则。获得这种规律性的一种可能的解决方案是在训练过程中引入显式正则化。因此，正如我们在本文的介绍中简要提到的，变分自动编码器可以定义为一种自动编码器，其训练经过正则化以避免过度拟合并确保潜在空间具有支持生成过程的良好属性。

Variational Autoencoders

就像标准自动编码器一样，变分自动编码器是一种由编码器和解码器组成的架构，经过训练以最小化编码解码数据与初始数据之间的重构误差。然而，为了引入潜在空间的一些正则化，我们对编码解码过程进行了轻微的修改：我们不是将输入编码为单个点，而是将其编码为潜在空间上的分布。然后模型的训练如下：

首先，输入被编码为潜在空间上的分布 the input is encoded as distribution over the latent space
第二，从该分布中采样潜在空间中的一个点 a point from the latent space is sampled from that distribution
第三，对采样点进行解码并计算重构误差 the sampled point is decoded and the reconstruction error can be computed
最后，重构误差通过网络反向传播 the reconstruction error is backpropagated through the network

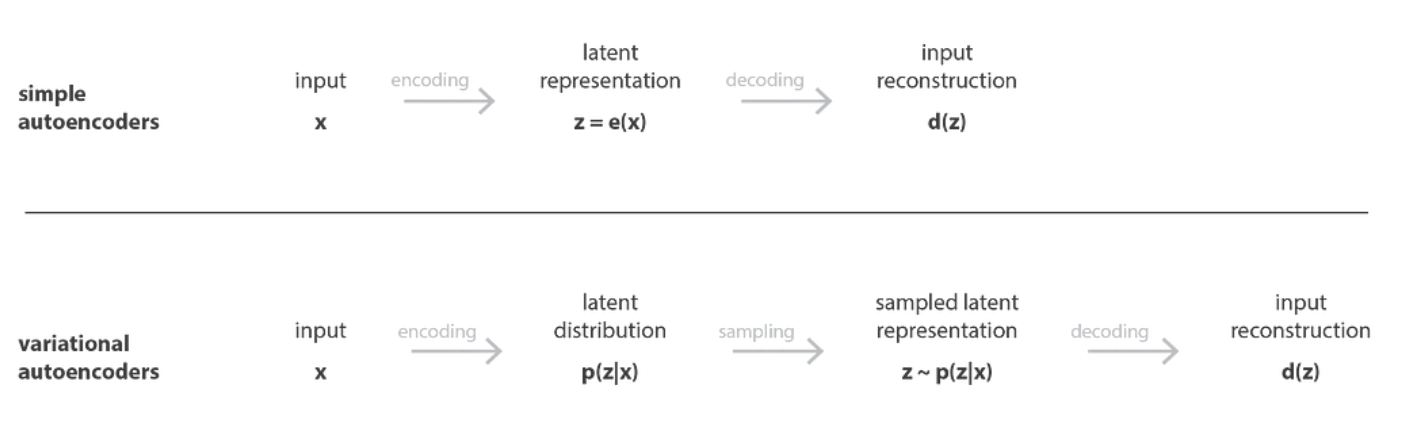
在实践中，编码的分布被选择为正态分布（Gaussian mixture distribution），以便编码器可以被训练以返回描述这些高斯分布的均值和协方差矩阵。输入被编码为具有一定方差而不是单点的分布的原因是，它可以非常自然地表达潜在空间正则化：编码器返回的分布被强制接近标准正态分布。我们将在下一小节中看到，我们以这种方式确保潜在空间的局部和全局正则化（局部是因为方差控制，全局是因为均值控制）。

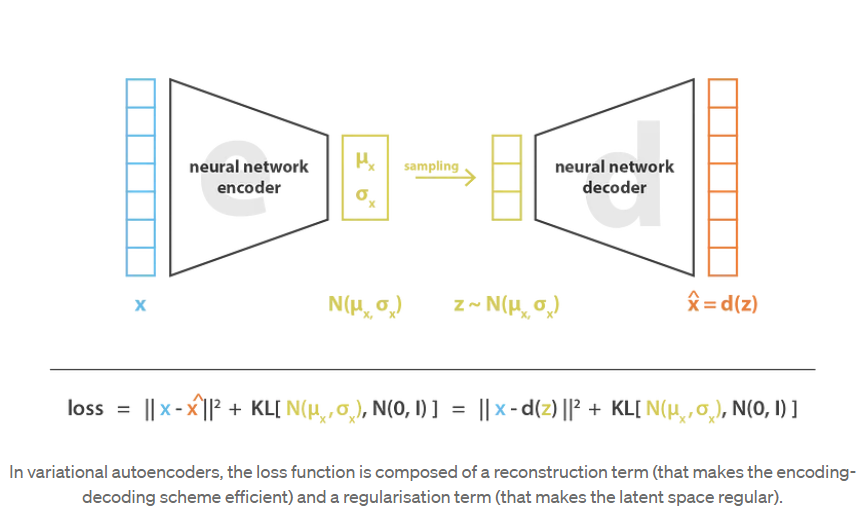
因此，在训练VAE时最小化的损失函数由一个“重构项”（ reconstruction error在解码器的最后一层上）和一个“正则化项”（latent error在编码器的最后一层上）组成。重构项倾向于使编码解码方案尽可能地具有高性能潜空间），通过使编码器返回的分布接近于标准正态分布，可以规范潜空间的连续性。而正则化项表示为返回的分布与标准高斯之间的 Kulback-Leibler（KL）散度（一种距离，用来衡量两个概率密度分布之间的差异，越小则差异越小）。这在下一节中将进一步说明。我们可以注意到，两个高斯分布之间的 Kulback-Leibler（KL）散度具有封闭形式，可以直接用两种分布的均值和协方差矩阵表示。

KL散度

考虑某个未知的分布 p(x)，假定用一个近似的分布 q(x) 对它进行建模。如果我们使用 q(x) 来建立一个编码体系，用来把 x 的值传给接收者，那么由于我们使用了q(x)而不是真实分布p(x)，平均编码长度比用真实分布p(x)进行编码增加的信息量(单位是 nat )为：

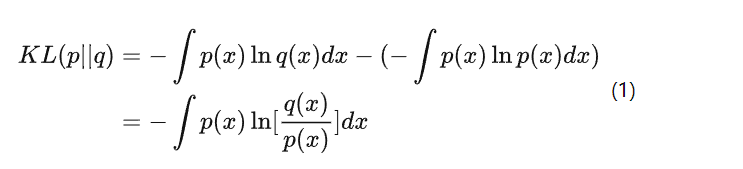
这被称为分布p(x)和分布q(x)之间的相对熵(relative entropy)或者KL散度( Kullback-Leibler divergence )。其中，交叉熵 $H(p, q)$ 指利用分布 $q$ 编码随机变量 $X$ 所需的编码长度，而熵 $H(p)$ 指编码随机变量 $X$ 所需的最优期望编码长度。

KL散度可以理解为 $p$ 和 $q$ 的交叉熵 $H(p, q) $与真实分布 $p$ 的熵 $H(p)$ 的差。最小化KL散度，可以令 $H(p, q) $与 $H(p)$ 接近，从而使得分布 $p$ 和 $q$ 变得相近。：

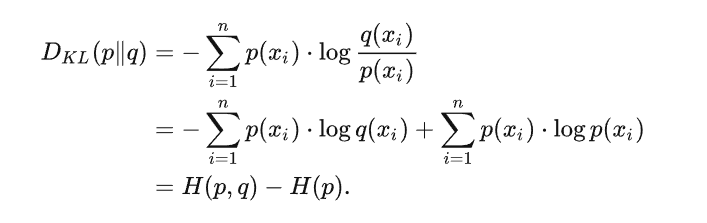
倘若我们优化KL散度，即是希望减小所需的额外编码数，使得分布 $p$ 和 $q$ 变得接近。这里有两种情况：

若真实分布 $p$ 恒定，那么优化KL散度等价于优化交叉熵，其目的是令交叉熵逼近最优期望编码长度，使得 $q$ 尽可能接近 $p$ 。在训练辨别模型时，往往是这种情况。为了简化计算，人们往往直接对交叉熵进行优化。
若真实分布 $p$ 不恒定，那么优化KL散度会同时改变交叉熵和熵的值，使得 $p$ 和 $q$ 相互接近。在训练生成模型时，往往是这种情况，为了使分布 $p$ 与 $q$ 相互接近，我们必须直接对KL散度进行优化。

Note：

KL散度恒大于0（显然用分布 $q$ 来对 $X$ 进行编码所需的编码长度一定是要比用真是分布 $p$ 进行编码的编码长度更长的）

最小化 KL 散度等价于最大化似然函数

关于正则化的直觉

潜在空间为了使生成过程可能发生而期望的规律性可以通过两个主要属性表示：连续性（潜在空间中的两个靠近的点解码后应该生成两个接近图像，比如下图右边三角形和圆角三角形）和完整性（针对选定的分布，从潜在空间采样的点在解码后应提供“有意义”的内容）。

VAE将输入编码为高斯分布而不是一个潜空间向量并不足以确保连续性和完整性。如果没有明确定义的正则化项，则模型可以学习以最小化其重构误差，从而“忽略”分布返回并表现得几乎像经典自动编码器（导致过度拟合）的事实。如果这样做，编码器可以返回具有微小变化的分布（倾向于punctual distributions），也可以返回具有非常不同的均值的分布（然后在潜空间中彼此相距相当远）。在这两种情况下，分布的被错误使用（取消了预期收益），并且不满足连续性和/或完整性。

因此，为了避免这些影响，我们必须对协方差矩阵和编码器返回的分布均值进行正则化。在实践中，通过强制分布接近标准正态分布（centred and reduced）来完成此正则化。这样，我们要求协方差矩阵接近于同一性，防止punctual distributions，并且均值接近于0，防止编码分布彼此相距太远。最终效果如下图右侧所示

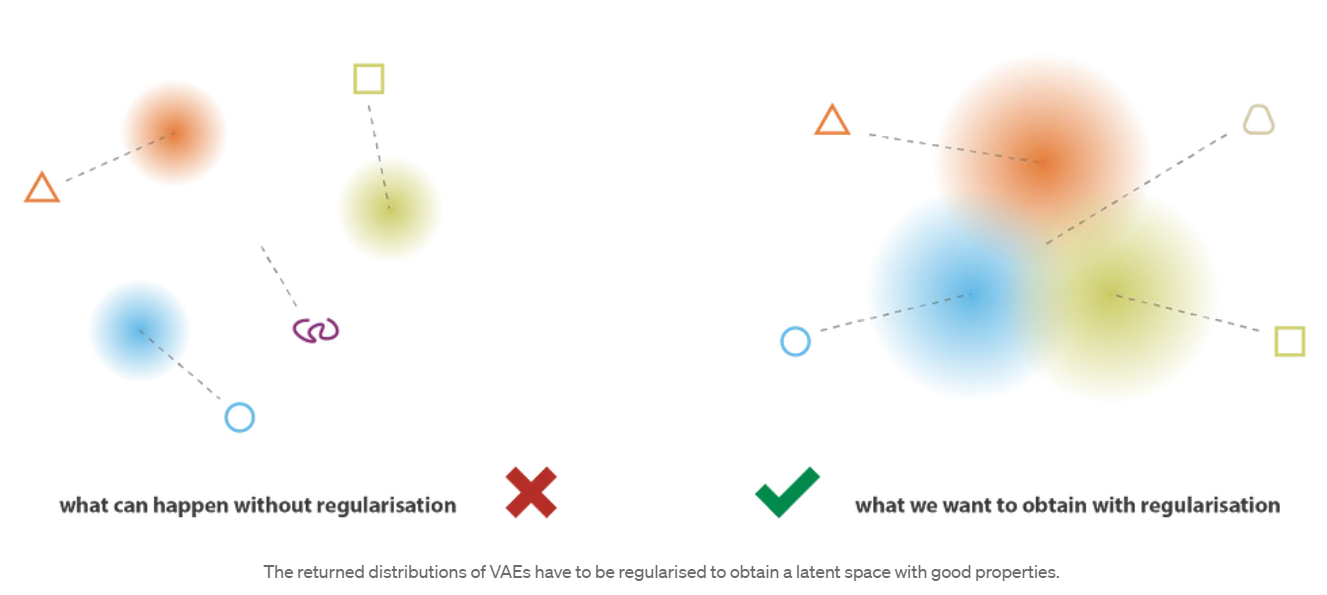
使用此正则化项，我们可以防止模型在潜在空间中对数据进行编码，并鼓励尽可能多的返回分布“重叠”，从而满足预期的连续性和完整性条件。当然，加入任何正则化项都是以训练数据上更高的解码器重建误差为代价的。但是，在重建误差与KL散度之间可以取得一个平衡，我们将在下一部分中看到如何从公式推导中自然得出平衡的表达。

总结这一小节，我们可以观察到，通过正则化获得的连续性和完整性往往会在潜在空间中编码的信息上产生“梯度”。例如，应将潜在空间中位于来自不同训练数据的两个编码分布的均值之间的中间点解码为提供第一个分布的数据与提供第二个分布的数据之间的某处，如下所示：在两种情况下，它都可以由自动编码器采样。

顺带一提，我们可以注意到我们提到的第二个潜在问题（网络使潜空间的向量之间彼此远离）在规模上变化几乎与第一个潜在问题（网络倾向于punctual distributions）：在两种情况下，分布方差相对于均值之间的距离都变小。

数学细节

在上一节中，我们给出了以下直观的概述：VAE是将输入编码为分布而不是点的自动编码器，并且其潜在空间“组织”通过将编码器返回的分布约束为接近标准高斯而得以规范化。在本节中，我们将对VAE进行更数学的介绍，这将使我们能够更严格地证明正则化项的合理性。为此，我们将建立一个明确的概率框架，并将特别使用变分推理技术。

概率框架和假设

首先，定义一个概率图形模型来描述我们的数据。我们用 x 表示代表我们的数据的变量，并假设x是由未直接观察到的潜在变量 z（编码表示）生成的。因此，对于每个数据点，假定以下两个步骤生成过程：

首先，从先验分布 $p(z)$ 中采样一个潜在表示 $z$
第二，从条件似然分布 $p(x | z)$ 采样数据 $x$

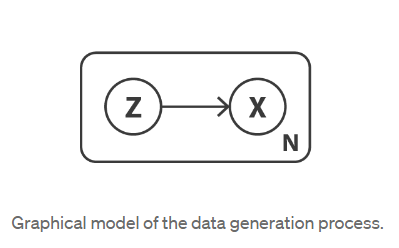
考虑到这种概率模型，我们可以重新定义编码器和解码器的概念。确实，与考虑确定性编码器和解码器的简单自动编码器相反，我们现在将考虑这两个对象的概率版本。自然地，“概率解码器”由 $p(x | z)$ ，它描述给定已编码变量的解码变量的分布，而“概率编码器”由 $p(z | x)$ 定义，它描述给定已编码变量的编码变量的分布。

在这一点上，我们已经注意到，在简单的自动编码器中所缺乏的潜在空间的正则化自然出现在数据生成过程的定义中：确实假设潜在空间中的编码表示 z 遵循先验分布 $p(z)$。这里提一下贝叶斯定理，该定理在先验 $p(z)$ ，似然性 $p(x | z)$ 和后验 $p(z | x)$ 之间建立联系。

\[p(z|x)=\frac {p(x|z)p(z)}{p(x)}=\frac{p(x|z)p(z)}{\int p(x|u)p(u)du} \]

现在让我们假设 $p(z)$是标准的高斯分布，$p(x | z)$是高斯分布，其均值由 z 变量的确定函数 f 定义，并且其协方差矩阵为 a 的形式乘以单位矩阵 I 的正常数 c。假定函数 f 属于表示为 F 的函数族，此族暂时未指定，稍后将选择。因此，我们有

\[\begin{array}{l}p(z)\equiv\mathcal{N}(0,I)\\ p(x|z)\equiv\mathcal{N}(f(z),cI)\quad f\in F\quad c>0\end{array} \]

现在，让我们考虑一下f的定义和固定。从理论上讲，我们知道 $p(z)$ 和 $p(x | z)$ ，我们可以使用贝叶斯定理来计算 $p(z | x)$ ：这是经典的贝叶斯推理问题。但是，正如我们在前一篇文章中所讨论的那样，这种计算通常是棘手的（由于分母处的积分），并且需要使用诸如变分推断之类的近似技术。

注意：在这里我们可以提到 $p(z)$ 和 $p(x | z)$ 都是高斯分布。因此，如果我们有 $E(x | z)= f(z) = z$，则意味着 $p(z | x)$ 也应遵循高斯分布，并且从理论上讲，我们可以“仅”尝试表示均值以及 $p(z | x)$ 的协方差矩阵相对于 $p(z)$ 和 $p(x | z)$ 的均值和协方差矩阵。但是，在实践中不能满足此条件，因此我们需要使用近似算法（如变分推理），使该方法相当通用，并且对模型假设的某些更改更加健壮。

变分公式推导

在统计中，变分推论（VI）是一种近似复杂分布的技术。这个想法是要设定一个参数化的分布族(parametrised family of distribution)（例如高斯族，其参数是均值和协方差），并寻找该族中我们目标分布的最佳近似值。该族中最好的元素是使给定的近似误差测量值最小化的元素（大多数情况下，近似值与目标之间的Kullback-Leibler差异），并通过描述该族的参数的梯度下降来发现。

在这里，我们将通过高斯分布 $q_x(z)$ 近似 $p(z | x)$ ，其均值和协方差由参数x的两个函数 g 和 h 定义。这两个函数应该分别属于函数 G 和 H的族，这将在以后指定，但是应该对其进行参数化。因此我们可以表示

\[\begin{array}{l}q_x(z)\equiv\mathcal{N}(g(x),h(x))\quad g\in G \quad h\in H\end{array} \]

因此，我们已经以这种方式定义了一个变分推论的候选者家族，现在需要通过优化函数 g 和 h（实际上是它们的参数）以最小化近似值和Kullback-Leibler之间的散度，从而找到该族中的最佳近似值。目标 $p(z | x)$。换句话说，我们正在寻找最优的 g *和 h *

\[\begin{aligned} \left(g^*, h^*\right) & =\underset{(g, h) \in G \times H}{\arg \min } K L\left(q_x(z), p(z \mid x)\right) \\ & =\underset{(g, h) \in G \times H}{\arg \min }\left(\mathbb{E}_{z \sim q_x}\left(\log q_x(z)\right)-\mathbb{E}_{z \sim q_x}\left(\log \frac{p(x \mid z) p(z)}{p(x)}\right)\right) \\ & =\underset{(g, h) \in G \times H}{\arg \min }\left(\mathbb{E}_{z \sim q_x}\left(\log q_x(z)\right)-\mathbb{E}_{z \sim q_x}(\log p(z))-\mathbb{E}_{z \sim q_x}(\log p(x \mid z))+\mathbb{E}_{z \sim q_x}(\log p(x))\right) \\ & =\underset{(g, h) \in G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_x}(\log p(x \mid z))-K L\left(q_x(z), p(z)\right)\right) \\ & =\underset{(g, h) \in G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_x}\left(-\frac{\|x-f(z)\|^2}{2 c}\right)-K L\left(q_x(z), p(z)\right)\right) \end{aligned} \]

在第二个等式中，我们可以观察到存在一个权衡点-近似后验 $p(z | x)$ 时-在最大化“观测”的可能性（预期的对数似然率，对于第一项）的最大化与保持之间接近先验分布（第二项 $q_x(z)$ 和 $p(z)$ 之间的KL散度最小）。这种折衷对于贝叶斯推理问题是很自然的，并表达了我们在数据的置信度与先前的置信度之间需要找到的平衡。

到目前为止，我们已经假设函数 f 是已知的并且是固定的，并且已经表明，在这种假设下，我们可以使用变分推断技术来近似后验 $p(z | x)$ 。然而，实际上，定义解码器的该函数 f 是未知的，并且还需要选择。我们的最初目标是找到一种性能良好的编解码方案，其潜空间足够规则以用于生成目的。如果规则性主要由潜在空间上假设的先验分布所决定，则整个编码-解码方案的性能高度取决于函数 f 的选择。确实，由于 $p(z | x)$ 可以从 $p(z)$ 和 $p(x|z)$ 近似（通过变分推论），并且 $p(z)$ 是简单的标准高斯模型，因此在我们的模型中，我们唯一可以使用的两个杠杆是参数 c（定义似然的方差）和函数 f（定义似然的均值）。我们可以在模型中使用参数 c（定义似然性的方差）和函数 f（定义似然性的平均值）进行优化。

因此，让我们考虑一下，正如我们之前讨论的那样，对于 F 中的任何函数 f（每个函数定义一个不同的概率解码器 $p(x|z)$ ，我们都可以得到 $p(z | x)$ 的最佳近似值，表示为 $q^*_x(z)$。尽管它具有概率性，但我们正在寻找一种尽可能高效的编码-解码方案，然后，当从 $q^*_x(z)$（ z 采样 z 时，给定 z，我们希望选择函数 f 使 x 的预期对数似然性最大化）。换句话说，对于给定的输入 x，当我们从分布 $q^*_x(z)$ 采样 z 然后从分布 $q^*_x(z)$ 采样 $x̂$ 时，我们希望最大化 $x̂ = x$ 的概率。因此，我们正在寻找最优f *。

\[\begin{aligned} f^* & =\underset{f \in F}{\arg \max } \mathbb{E}_{z \sim q_x^*}(\log p(x \mid z)) \\ & =\underset{f \in F}{\arg \max } \mathbb{E}_{z \sim q_x^*}\left(-\frac{\|x-f(z)\|^2}{2 c}\right) \end{aligned} \]

其中 $q^*_x(z)$取决于函数 f，如前所述获得。将所有部分聚集在一起，我们正在寻找最优的f *，g *和h *，以便

\[\left(f^*, g^*, h^*\right)=\underset{(f, g, h) \in F \times G \times H}{\arg \max }\left(\mathbb{E}_{z \sim q_x}\left(-\frac{\|x-f(z)\|^2}{2 c}\right)-K L\left(q_x(z), p(z)\right)\right) \]

我们可以在此目标函数中确定上一节中对VAE的直观描述中引入的元素：$x$ 和 $f(z)$ 之间的重构误差以及 $q_x(z)$ 和 $p(z)$ （z之间的KL散度给出的正则化项）（这是标准的高斯）。我们还可以注意到常数 c，它决定了前两个条件之间的平衡。 c 越高，我们对模型中的概率解码器假设 $f(z)$ 周围的方差就越大，因此，相对于重构项，我们更倾向于正则化项（如果 c 低，则相反）。

将神经网络引入模型

至此，我们已经建立了一个概率模型，该模型依赖于三个函数 f，g和h，并使用变分推理表示要解决的优化问题，以便获得能够给出最优值的f*，g*和h*。从而给出该模型的最佳编码-解码方案。。

由于我们无法轻松地在函数的整个空间上进行优化，因此我们限制了优化域，并决定将f，g和h表示为神经网络。因此，F，G和H分别对应于网络体系结构定义的功能族，并且对这些网络的参数进行了优化。

实际上，g和h不是由两个完全独立的网络定义的，而是共享它们的一部分架构和权重

\[g(x)=g_2(g_1(x)) \quad h(x)=h_2(h_1(x)) \quad g_1(x)=h_1(x) \]

由于定义了 $q_x(z)$ 的协方差矩阵，因此 $h(x)$ 被假定为方矩阵。但是，为了简化计算并减少参数的数量，我们做出了附加假设，即我们的 $p(z | x)$ 近似值 $q_x(z)$ 是具有对角协方差矩阵的多维高斯分布（变量独立性假设）。在此假设下， $h(x)$ 只是协方差矩阵对角元素的向量，因此其大小与 $g(x)$ 相同。但是，我们以这种方式减少了我们考虑用于变化推断的分布族，因此，获得的 $p(z | x)$ 的近似值可能不太准确。

与对 $p(z | x)$ 建模并考虑均值和协方差均是 x（g和h）的函数的高斯模型的编码器部分相反，我们的模型假设 $p(x | z)$ 为固定的高斯模型协方差。定义高斯平均值的变量z的函数f由神经网络建模。

然后，通过将编码器和解码器部分串联在一起，可以获得总体架构。但是，在训练过程中，我们仍然需要非常小心从编码器返回的分布中进行采样的方式。采样过程必须以允许错误通过网络反向传播的方式表示。尽管有随机抽样发生在体系结构的中间，但有一个简单的技巧称为重新参数化技巧，该技巧使梯度下降成为可能，并且包括以下事实：如果z是遵循均值为 $g(x)$ 的高斯分布的随机变量，协方差为 $H(x)=h(x).h^t(x)$ 则可以表示为

\[z=h(x)\zeta+g(x)\quad \zeta \sim \mathcal{N}(0, I) \]

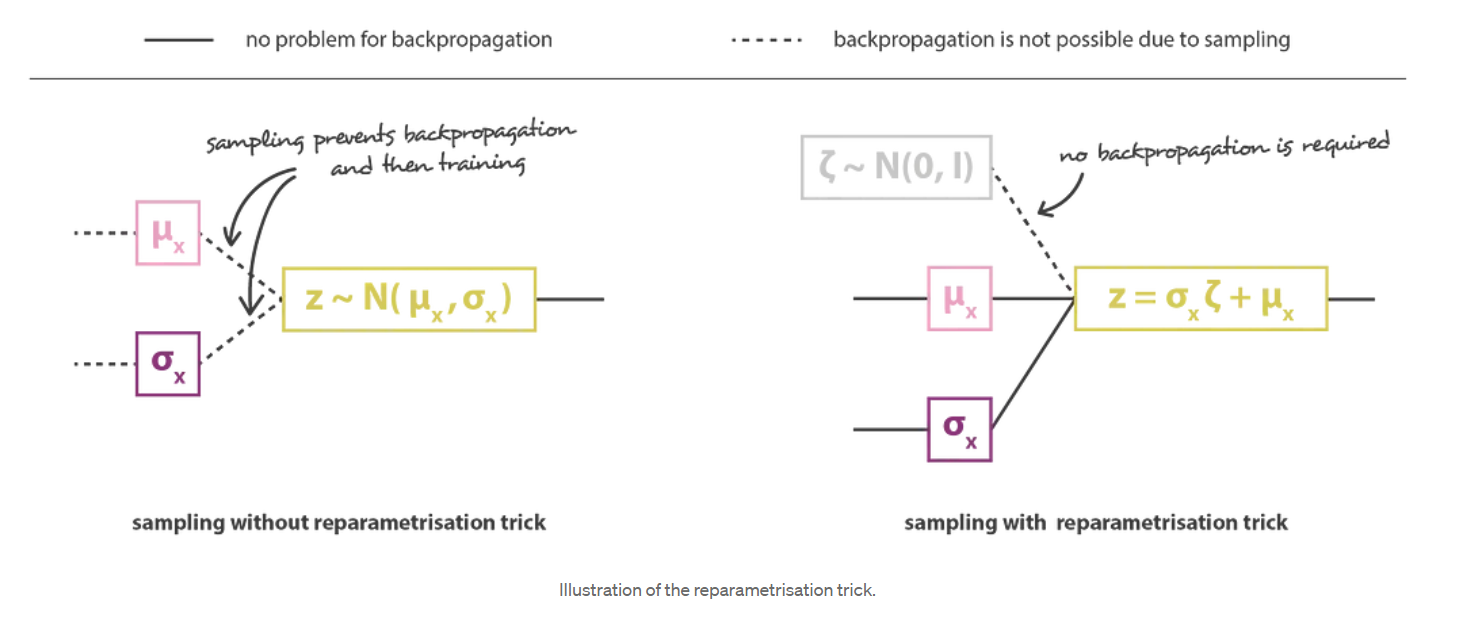
最后，这种方式获得的变分式自动编码器架构的目标函数由上一小节的最后一个方程式给出，在该方程式中，理论上的期望值或多或少地被精确的蒙特卡洛近似所取代，该近似值在大多数情况下包含在单次抽奖。因此，考虑此近似值并表示 $C = 1 /(2c)$，我们得到了上一节中直观得出的损失函数，该函数由一个重构项，一个正则项和一个常数来定义这两项的相对权重。

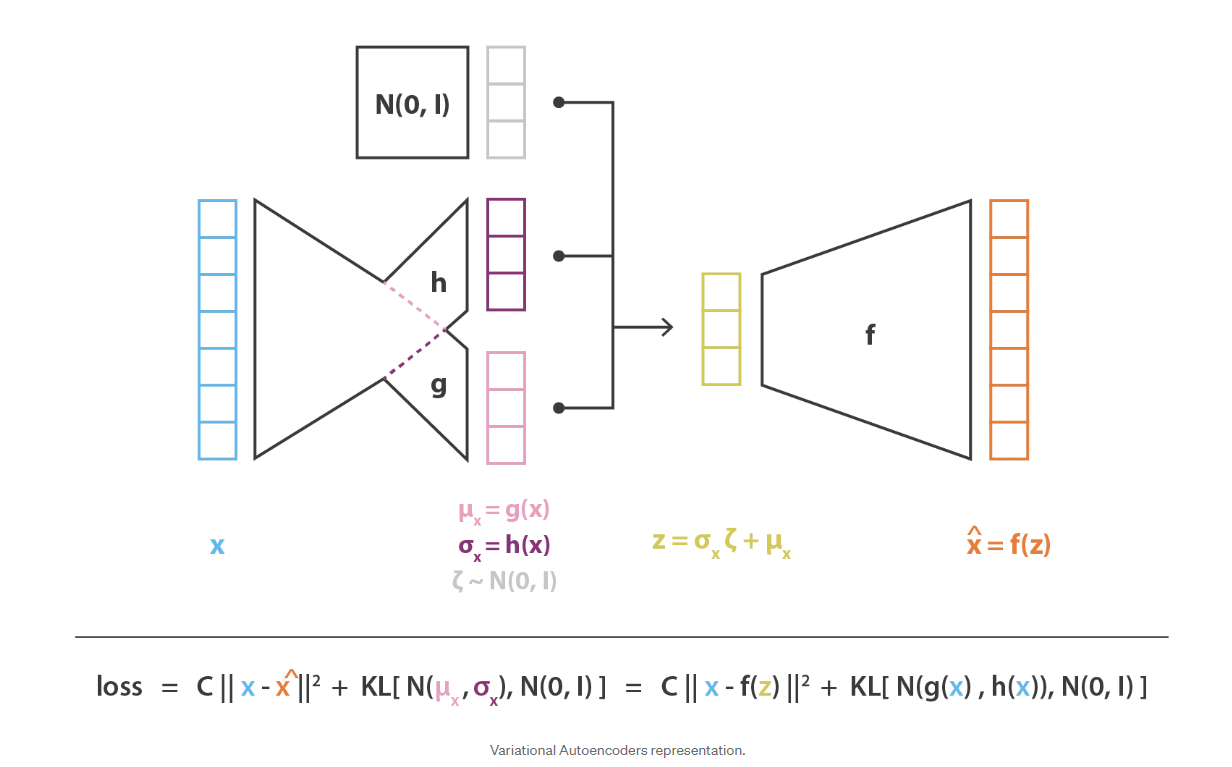
要点（Takeaways）

The main takeways of this article are:

dimensionality reduction is the process of reducing the number of features that describe some data (either by selecting only a subset of the initial features or by combining them into a reduced number new features) and, so, can be seen as an encoding process
autoencoders are neural networks architectures composed of both an encoder and a decoder that create a bottleneck to go through for data and that are trained to lose a minimal quantity of information during the encoding-decoding process (training by gradient descent iterations with the goal to reduce the reconstruction error)
due to overfitting, the latent space of an autoencoder can be extremely irregular (close points in latent space can give very different decoded data, some point of the latent space can give meaningless content once decoded, …) and, so, we can’t really define a generative process that simply consists to sample a point from the latent space and make it go through the decoder to get a new data
variational autoencoders (VAEs) are autoencoders that tackle the problem of the latent space irregularity by making the encoder return a distribution over the latent space instead of a single point and by adding in the loss function a regularisation term over that returned distribution in order to ensure a better organisation of the latent space
assuming a simple underlying probabilistic model to describe our data, the pretty intuitive loss function of VAEs, composed of a reconstruction term and a regularisation term, can be carefully derived, using in particular the statistical technique of variational inference (hence the name “variational” autoencoders)