title: DAA HW
Classical Sort
Insertion sort
n = 6
L = [1, 2, 3, 5 ,10, 4]
# n = int(input())
# L = [int(x) for x in input().split()]
def insertion_sort(L):
n = len(L)
for i in range(n):
for j in range(i, 0, -1):
if L[j - 1] > L[j]:
L[j - 1], L[j] = L[j], L[j - 1]
return L
insertion_sort(L)
[1, 2, 3, 4, 5, 10]
Selection sort
n = 6
L = [1, 2, 3, 5 ,10, 4]
# n = int(input())
# L = [int(x) for x in input().split()]
def selection_sort(L):
n = len(L)
for i in range(n - 1):
# print(L[i: n + 1])
min_val = min(L[i: n + 1])
# print(min_val)
min_index = L.index(min_val)
L[i], L[min_index] = L[min_index], L[i]
return L
selection_sort(L)
[1, 2, 3, 4, 5, 10]
Bubble sort
n = 6
L = [1, 2, 3, 5 ,10, 4]
# n = int(input())
# L = [int(x) for x in input().split()]
def bubble_sort(L):
n = len(L)
for i in range(n):
for j in range(1, i + 1):
if L[j - 1] > L[j]:
L[j - 1], L[j] = L[j], L[j - 1]
return L
bubble_sort(L)
[1, 2, 3, 5, 4, 10]
Merge sort
n = 6
L = [1, 2, 3, 5 ,10, 4]
from heapq import merge
def merge_sort(L):
if len(L) < 2:
return L
mid = int(len(L)/2)
L1 = merge_sort(L[:mid])
L2 = merge_sort(L[mid:])
return list(merge(L1, L2))
LL = merge_sort(L)
print(LL)
[1, 2, 3, 4, 5, 10]
import pandas as pd
from timeit import default_timer as tic
from timeit import default_timer as toc
def poipoi(n):
L = [x for x in range(n, 0, -1)]
cur = []
cur.append(n)
start = tic()
insertion_sort(L)
end = toc()
cur.append(end - start)
start = tic()
selection_sort(L)
end = toc()
cur.append(end - start)
start = tic()
bubble_sort(L)
end = toc()
cur.append(end - start)
start = tic()
merge_sort(L)
end = toc()
cur.append(end - start)
return cur
import numpy as np
matrix = []
for nn in range(1, 11):
n = nn * 1000
cur = poipoi(n)
matrix.append(cur)
matrix = np.array(matrix)
col = ['n', 'insertion', 'selection', 'bubble', 'merge']
df = pd.DataFrame(matrix, columns = col)
df.style.hide_index()
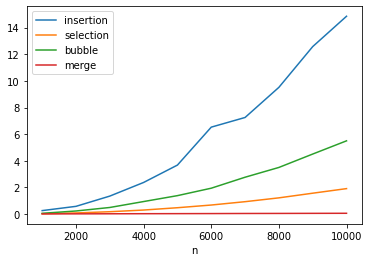
| n | insertion | selection | bubble | merge |
|---|---|---|---|---|
| 1000.000000 | 0.253705 | 0.018792 | 0.050956 | 0.004787 |
| 2000.000000 | 0.573651 | 0.077297 | 0.224771 | 0.009916 |
| 3000.000000 | 1.344024 | 0.170123 | 0.488674 | 0.014862 |
| 4000.000000 | 2.368482 | 0.295751 | 0.934055 | 0.021222 |
| 5000.000000 | 3.674450 | 0.469937 | 1.377981 | 0.025488 |
| 6000.000000 | 6.524600 | 0.672289 | 1.937233 | 0.030519 |
| 7000.000000 | 7.250596 | 0.924020 | 2.761573 | 0.037561 |
| 8000.000000 | 9.514974 | 1.211665 | 3.496719 | 0.041284 |
| 9000.000000 | 12.575886 | 1.561482 | 4.502677 | 0.047156 |
| 10000.000000 | 14.856315 | 1.905542 | 5.495838 | 0.052396 |
Runtime
df.plot(x = 'n', y = col[1:], kind = 'line')
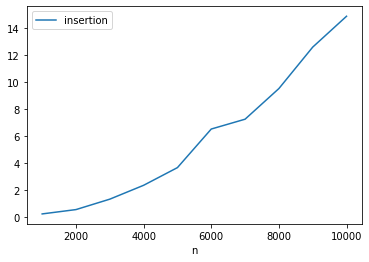
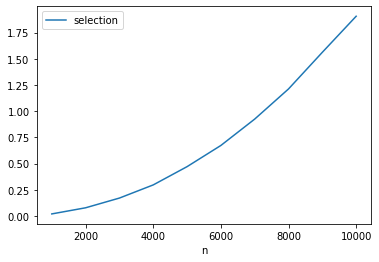
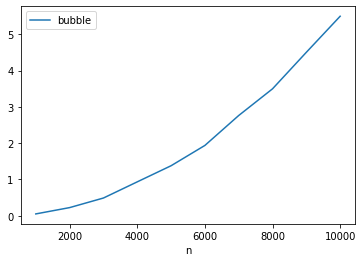
for i in range(4):
df.plot(x = 'n', y = col[i + 1], kind = 'line')
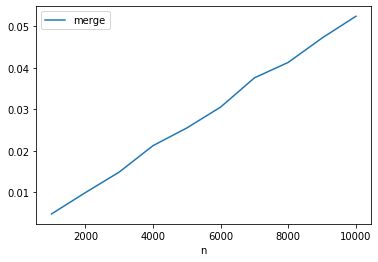
Divide and Conquer
Binary Search
def binary_search(L, tar):
l = 0
r = len(L) - 1
while(l <= r):
mid = int((l + r) / 2)
if L[mid] == tar:
return mid
if L[mid] > tar:
r = mid - 1
continue
if L[mid] < tar:
l = mid + 1
continue
return -1
example = [15,20,14,10,18, 22, 90, 100]
example.sort()
print(example)
binary_search(example, 90)
[10, 14, 15, 18, 20, 22, 90, 100]
6
import numpy as np
A = np.array([[1, 1], [1, 0]])
def power(A, n):
if n == 0:
return np.identity(2)
if n == 1:
return A
if n % 2 == 0:
return power(A, int(n/2)).dot( power(A, int(n/2)))
return (power(A, int(n/2)).dot( power(A, int(n/2)))).dot(A)
print(power(A, 0))
print(power(A, 5))
print(power(A, 10))
[[1. 0.]
[0. 1.]]
[[8 5]
[5 3]]
[[89 55]
[55 34]]
Maximum Subarray
example = [-2, 11, -4, 13, -5, -2]
def find_max_cross_subarray(a, low, mid, high):
left_sum = -0x7fffffff
sum = 0
for i in range(mid, low - 1, -1):
sum += a[i]
if sum > left_sum:
left_sum = sum
max_left = i
right_sum = -0x7fffffff
sum = 0
for i in range(mid + 1, high + 1):
sum += a[i]
if sum > right_sum:
right_sum = sum
max_right = i
return max_left, max_right, left_sum + right_sum
def find_max_subarray(a, low, high):
if high == low:
return low, high, a[low]
mid = int((high + low) / 2)
left_low, left_high, left_sum = find_max_subarray(a, low, mid)
right_low, right_high, right_sum = find_max_subarray(a, mid + 1, high)
cross_low, cross_high, cross_sum = find_max_cross_subarray(a, low, mid, high)
if left_sum >= right_sum and left_sum >= cross_sum:
return left_low, left_high, left_sum
if right_sum >= left_sum and right_sum >= cross_sum:
return right_low, right_high, right_sum
return cross_low, cross_high, cross_sum
find_max_subarray(example, 0, len(example)-1)
(1, 3, 20)
Strassen’s algorithm for matrix multiplication
square matraces, any dimension
import random
import numpy as np
ss = (10,10)
A = np.random.randint(10, size=ss)
B = np.random.randint(10, size=ss)
print(A.dot(B))
def padd(A):
sp = A.shape
n = sp[0]
A = np.concatenate((A, np.zeros((n, 1))), axis=1)
A = np.concatenate((A, np.zeros((1, n + 1))), axis=0)
return A
def dell(A):
sp = A.shape
# print(sp)
# print(A)
n = sp[0]
A = np.delete(A, n - 1, 0)
A = np.delete(A, n - 1, 1)
return A
def mat_mul(A, B):
sp = A.shape
n = sp[0] - 1
if n == 0:
return A.dot(B)
flag = 0
if (n + 1) % 2 != 0:
A = padd(A)
B = padd(B)
flag = 1
sp = A.shape
n = sp[0] - 1
mid = int(n / 2) + 1
A11 = A[:mid, :mid]
A12 = A[:mid, mid:]
A21 = A[mid:, :mid]
A22 = A[mid:, mid:]
B11 = B[:mid, :mid]
B12 = B[:mid, mid:]
B21 = B[mid:, :mid]
B22 = B[mid:, mid:]
S1 = B12 - B22
S2 = A11 + A12
S3 = A21 + A22
S4 = B21 - B11
S5 = A11 + A22
S6 = B11 + B22
S7 = A12 - A22
S8 = B21 + B22
S9 = A11 - A21
S10 = B11 + B12
P1 = mat_mul(A11, S1)
P2 = mat_mul(S2, B22)
P3 = mat_mul(S3, B11)
P4 = mat_mul(A22, S4)
P5 = mat_mul(S5, S6)
P6 = mat_mul(S7, S8)
P7 = mat_mul(S9, S10)
C11 = P5 + P4 - P2 + P6
C12 = P1 + P2
C21 = P3 + P4
C22 = P5 + P1 - P3 - P7
if not flag:
return np.bmat([[C11, C12], [C21, C22]])
R = np.bmat([[C11, C12], [C21, C22]])
R = dell(R)
return R
print(mat_mul(A, B))
[[170 198 225 211 227 282 306 330 295 174]
[145 187 150 201 195 178 248 240 218 140]
[171 251 276 234 267 308 380 373 337 191]
[158 204 215 240 284 246 245 276 278 126]
[176 215 167 251 255 215 263 285 281 140]
[134 152 231 170 203 233 277 291 261 156]
[ 98 111 135 158 197 129 163 188 156 85]
[ 79 115 146 117 142 138 189 173 143 120]
[167 250 239 266 262 222 332 308 350 180]
[101 124 92 141 139 106 162 157 139 94]]
[[170. 198. 225. 211. 227. 282. 306. 330. 295. 174.]
[145. 187. 150. 201. 195. 178. 248. 240. 218. 140.]
[171. 251. 276. 234. 267. 308. 380. 373. 337. 191.]
[158. 204. 215. 240. 284. 246. 245. 276. 278. 126.]
[176. 215. 167. 251. 255. 215. 263. 285. 281. 140.]
[134. 152. 231. 170. 203. 233. 277. 291. 261. 156.]
[ 98. 111. 135. 158. 197. 129. 163. 188. 156. 85.]
[ 79. 115. 146. 117. 142. 138. 189. 173. 143. 120.]
[167. 250. 239. 266. 262. 222. 332. 308. 350. 180.]
[101. 124. 92. 141. 139. 106. 162. 157. 139. 94.]]
Randomized Quick Sort
import random
def part(l, r, a):
rd_ind = random.randint(l, r + 1)
a[l], a[rd_ind] = a[rd_ind], a[l]
pivot, p = a[l], r
for i in range(r, l, -1):
if a[i] >= pivot:
a[i], a[p] = a[p], a[i]
print(a)
p -= 1
a[p], a[l] = a[l], a[p]
print(a)
return p
def quicksort(l, r, a):
if len(a) == 1:
return a
if l < r:
pi = part(l, r, a)
quicksort(l, pi-1, a)
quicksort(pi+1, r, a)
return a
example = [15,20,14,10,18]
print(quicksort(0, len(example)-1, example))
[15, 20, 14, 10, 18]
[15, 10, 14, 20, 18]
[14, 10, 15, 20, 18]
[10, 14, 15, 20, 18]
[10, 14, 15, 18, 20]
[10, 14, 15, 18, 20]
[10, 14, 15, 18, 20]
Dynamic Programming
Rod cutting problem (Both Top-down and Bottom-up)
# top-down
INF = 0x7fffffff
def memo_cut_rod(p, n):
r = [-INF for x in range(0, n + 1)]
return memo_cut_rod_aux(p, n, r)
def memo_cut_rod_aux(p, n, r):
if(r[n]) >= 0:
return r[n]
if n == 0:
q = 0
else:
q = -INF
for i in range(1, n + 1):
q = max(q, p[i] + memo_cut_rod_aux(p, n - i, r))
r[n] = q
return q
def bt_up_cut_rod(p, n):
r = [0 for x in range(0, n + 1)]
r[0] = 0
for j in range(1, n + 1):
q = -INF
for i in range (1, j + 1):
q = max(q, p[i] + r[j - i])
r[j] = q
return r[n]
def ext_bt_up_cut_rod(p, n):
r = [0 for x in range(0, n + 1)]
s = [0 for x in range(0, n + 1)]
for j in range(1, n + 1):
q = -INF
for i in range(1, j + 1):
if q < p[i] + r[j - i]:
q = p[i] + r[j - i]
s[j] = i
r[j] = q
return r, s
def print_cut_rod_sol(p, n):
r, s = ext_bt_up_cut_rod(p, n)
print(r)
print(s)
while n > 0:
print(s[n])
n = n - s[n]
p=[-INF, 1, 5, 8, 9 , 10 , 17, 17 ,20]
n = len(p) - 1
ans_bt = bt_up_cut_rod(p, n)
ans_tp = memo_cut_rod(p, n)
print(ans_bt)
print(ans_tp)
print_cut_rod_sol(p, n)
22
22
[0, 1, 5, 8, 10, 13, 17, 18, 22]
[0, 1, 2, 3, 2, 2, 6, 1, 2]
2
6
p = [-INF, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
n = len(p) - 1
ans_bt = bt_up_cut_rod(p, n)
ans_tp = memo_cut_rod(p, n)
print(ans_bt)
print(ans_tp)
print_cut_rod_sol(p, n)
30
30
[0, 1, 5, 8, 10, 13, 17, 18, 22, 25, 30]
[0, 1, 2, 3, 2, 2, 6, 1, 2, 3, 10]
10
Matrix chain multiplication problem (Bottom-up)
def matrix_chain_order(p):
# n = len(p) - 1
n = len(p) - 2
aux_a = [0 for x in range(0, n + 1)]
m = [aux_a for x in range(0, n + 1)]
s = [aux_a for x in range(0, n + 1)]
for l in range(2, n + 1):
for i in range(1, n - l + 1 + 1):
j = i + l - 1
m[i][j] = -INF
for k in range(i, j - 1 + 1):
q = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j]
if q < m[i][j]:
m[i][j] = q
s[i][j] = k
return m, s
def print_optimal_parens(s, i, j):
if i == j:
print("A_" + str(i), end='')
else:
print("(", end='')
print_optimal_parens(s, i, s[i][j])
print_optimal_parens(s, s[i][j] + 1, j)
print(")", end='')
m, s = matrix_chain_order(p)
print_optimal_parens(s, 1, len(p) - 2)
((((((((A_1A_2)A_3)A_4)A_5)A_6)A_7)A_8)A_9)
Longest common subsequence (Bottom-up)
def lcs_length(x, y):
m = len(x) - 1
n = len(y) - 1
# aux_a = [0 for x in range(n + 1)]
b = [[0 for x in range(n + 1)] for x in range(m + 1)]
c = [[0 for x in range(n + 1)] for x in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if x[i] == y[j]:
c[i][j] = c[i - 1][j - 1] + 1
b[i][j] = 1
elif c[i - 1][j] >= c[i][j - 1]:
c[i][j] = c[i - 1][j]
b[i][j] = 2
else:
c[i][j] = c[i][j - 1]
b[i][j] = 3
return c, b
def print_lcs(b, x, i, j):
if i == 0 or j ==0:
return
if b[i][j] == 1:
print_lcs(b, x, i - 1, j - 1)
print(x[i], end='')
elif b[i][j] == 2:
print_lcs(b, x, i - 1, j)
else:
print_lcs(b, x, i, j - 1)
x = ['0','A', 'B', 'C', 'B', 'D', 'A', 'B']
y = ['0','B', 'D', 'C', 'A', 'B', 'A']
c, b = lcs_length(x, y)
print(c)
print(b)
print_lcs(b, x, len(x) - 1, len(y) - 1)
[[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 1], [0, 1, 1, 1, 1, 2, 2], [0, 1, 1, 2, 2, 2, 2], [0, 1, 1, 2, 2, 3, 3], [0, 1, 2, 2, 2, 3, 3], [0, 1, 2, 2, 3, 3, 4], [0, 1, 2, 2, 3, 4, 4]]
[[0, 0, 0, 0, 0, 0, 0], [0, 2, 2, 2, 1, 3, 1], [0, 1, 3, 3, 2, 1, 3], [0, 2, 2, 1, 3, 2, 2], [0, 1, 2, 2, 2, 1, 3], [0, 2, 1, 2, 2, 2, 2], [0, 2, 2, 2, 1, 2, 1], [0, 1, 2, 2, 2, 1, 2]]
BCBA
0-1 Knapsack problem (Bottom-up)
def knapsack(v, w, W):
n = len(w)
w = [INF] + w
v = [-INF] + v
m = [[0 for x in range(W + 3)] for x in range(0, n + 3)]
# m = [[0 for x in range(n + 2)] for x in range(0, W + 2)]
j_max = min(w[n] - 1, W)
for j in range(j_max + 1):
m[n][j] = 0
for j in range(w[n], W + 1):
m[n][j] = v[n]
for i in range(n - 1, 2 - 1, -1):
j_max = min(w[i] - 1, W)
for j in range(j_max + 1):
m[i][j] = m[i + 1][j]
for j in range(w[i], W + 1):
m[i][j] = max(m[i + 1][j], m[i + 1][j - w[i]] + v[i])
m[1][W] = m[2][W]
if W >= w[1]:
m[1][W] = max(m[1][W], m[2][W - w[1]] + v[1])
return m
def trace_back(m, w, W):
n = len(w)
x = [0 for x in range(n + 1)]
w = [INF] + w
for i in range(1, n - 1 + 1):
if m[i][W] == m[i + 1][W]:
x[i] = 0
else:
x[i] = 1
W = W - w[i]
if W >= w[n]:
x[n] = 1
else:
x[n] = 0
x = x[1:]
return x
W = 12
w = [4, 6, 2, 2, 5, 1]
v = [8, 10, 6, 3, 7, 2]
m = knapsack(v, w, W)
print(w)
x = trace_back(m, w, W)
print(x)
print(v)
print(m[1][W])
[4, 6, 2, 2, 5, 1]
[1, 1, 1, 0, 0, 0]
[8, 10, 6, 3, 7, 2]
24
w = [3, 4, 6, 5]
v = [2, 3, 1, 4]
W = 8
m = knapsack(v, w, W)
print(w)
x = trace_back(m, w, W)
print(x)
print(v)
print(m[1][W])
[3, 4, 6, 5]
[1, 0, 0, 1]
[2, 3, 1, 4]
6
w = 10
def foo(w):
w = w + 10
print(foo(10))
None
Heap and Linear Sort
Theory part
!pip install igraph
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: igraph in /usr/local/lib/python3.8/dist-packages (0.10.2)
Requirement already satisfied: texttable>=1.6.2 in /usr/local/lib/python3.8/dist-packages (from igraph) (1.6.7)
import igraph as ig
import matplotlib.pyplot as plt
def left(i):
return 2 * (i + 1) - 1
def right(i):
return 2 * (i + 1)
def show_tree(X):
n_vertices = len(X)
edges = []
hs = len(X)
for i in range(int(len(X)/2) ):
if left(i) < hs:
edges.append((i, left(i)))
if right(i) < hs:
edges.append((i, right(i)))
Xs = [str(int) for int in X]
B = ["(" + str(i) + ")" + Xs[i] for i in range(len(X))]
g = ig.Graph(n_vertices, edges)
g.vs["name"] = X #!!!!
fig, ax = plt.subplots(figsize=(3,3))
layout = g.layout_reingold_tilford(root=[0])
ig.plot(
g,
target=ax,
layout=layout,
vertex_size=0.7,
vertex_color="white",
vertex_frame_width=0.7,
vertex_frame_color="black",
vertex_label=g.vs["name"],
vertex_label_size=12.0,
)
plt.show()
max_heapify
def max_heapify(A, i):
hs = len(A)
l = left(i)
r = right(i)
if l < hs and A[l] > A[i]:
largest = l
else:
largest = i
if r < hs and A[r] > A[largest]:
largest = r
if largest != i :
# show_tree(A)
A[i], A[largest] = A[largest], A[i]
max_heapify(A, largest)
build_max_heap
def build_max_heap(A):
for i in range(int(len(A)/2)-1, -1, -1):
# print(i)
max_heapify(A, i)
X = [4,1,3,2,16,9,10,14,8,7]
build_max_heap(X)
show_tree(X)
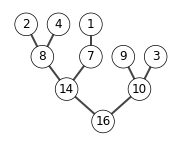
heap_sort
def heap_sort(A):
# print("build max heap")
build_max_heap(A)
# print("extracting elements from A")
hs = len(A)
B = []
for i in range(len(A) - 1, 0, -1):
B.append(A[0])
# print(B)
A = A[1:]
max_heapify(A, 0)
return B
X = [4,1,3,2,16,9,10,14,8,7]
print(heap_sort(X))
[16, 14, 10, 9, 8, 7, 4, 3, 2]
counting sort
def counting_sort(A):
INF = 0x7fffffff
n = len(A)
k = max(A)
C = [0 for i in range(k + 1)]
B = [0 for i in range(len(A))]
for j in range(n):
C[A[j]] += 1
for i in range(1, k + 1):
C[i] += C[i - 1]
for j in range(n - 1, -1, -1):
B[C[A[j]] - 1] = A[j]
C[A[j]] -= 1
return B
A = [300, 324, 311, 325, 308, 324];
print(counting_sort(A))
[300, 308, 311, 324, 324, 325]
radix sort
from IPython.core.events import post_execute
def get_max_digit(A):
x = max(A)
i = 0
while x != 0:
x = int(x / 10)
i += 1
return i
def counting_sort_for_radix(A, Ad):
INF = 0x7fffffff
n = len(A)
k = max(A)
C = [0 for i in range(k + 1)]
B = [0 for i in range(len(A))]
for j in range(n):
C[Ad[j]] += 1
for i in range(1, k + 1):
C[i] += C[i - 1]
for j in range(n - 1, -1, -1):
B[C[Ad[j]] - 1] = A[j]
C[Ad[j]] -= 1
return B
def radix_sort(A, d):
# A = np.array(A)
for i in range(d):
B = [x // (10 ** i) for x in A]
B = [x % (10) for x in B]
print(B)
A = counting_sort_for_radix(A, B)
return A
def radix_for_negative(A):
negative_part = []
positive_part = []
for i in range(len(A)):
if A[i] < 0:
negative_part = negative_part + [A[i]]
else:
positive_part = positive_part + [A[i]]
negative_part = [-x for x in negative_part]
print(positive_part)
print(negative_part)
d_negative = get_max_digit(negative_part)
d_positive = get_max_digit(positive_part)
negative_part = radix_sort(negative_part, d_negative)
positive_part = radix_sort(positive_part, d_positive)
negative_part = [-x for x in negative_part]
negative_part = negative_part[::-1]
return negative_part + positive_part
A = [329, 457, 1657, 39, 4, 63]
d = get_max_digit(A)
radix_sort(A, d)
[9, 7, 7, 9, 4, 3]
[6, 0, 5, 5, 2, 3]
[0, 3, 0, 4, 6, 0]
[0, 0, 0, 0, 0, 1]
[4, 39, 63, 329, 457, 1657]
A = [329, 457,89, 436, 63, 7,0]
d = get_max_digit(A)
radix_sort(A, d)
[9, 7, 9, 6, 3, 7, 0]
[0, 6, 3, 5, 0, 2, 8]
[0, 0, 3, 4, 4, 0, 0]
[0, 7, 63, 89, 329, 436, 457]
A = [329, 457,89, -436,- 63, 7,0]
radix_for_negative(A)
[329, 457, 89, 7, 0]
[436, 63]
[6, 3]
[6, 3]
[4, 0]
[9, 7, 9, 7, 0]
[0, 5, 0, 2, 8]
[0, 0, 3, 4, 0]
[-436, -63, 0, 7, 89, 329, 457]
max(A)
457
Code part
!pip install igraph
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: igraph in /usr/local/lib/python3.7/dist-packages (0.10.2)
Requirement already satisfied: texttable>=1.6.2 in /usr/local/lib/python3.7/dist-packages (from igraph) (1.6.7)
import igraph as ig
import matplotlib.pyplot as plt
def left(i):
return 2 * (i + 1) - 1
def right(i):
return 2 * (i + 1)
def show_tree(X):
n_vertices = len(X)
edges = []
hs = len(X)
for i in range(int(len(X)/2) ):
if left(i) < hs:
edges.append((i, left(i)))
if right(i) < hs:
edges.append((i, right(i)))
Xs = [str(int) for int in X]
B = ["(" + str(i) + ")" + Xs[i] for i in range(len(X))]
g = ig.Graph(n_vertices, edges)
g.vs["name"] = X #!!!!
fig, ax = plt.subplots(figsize=(3,3))
layout = g.layout_reingold_tilford(root=[0])
ig.plot(
g,
target=ax,
layout=layout,
vertex_size=0.7,
vertex_color="white",
vertex_frame_width=0.7,
vertex_frame_color="black",
vertex_label=g.vs["name"],
vertex_label_size=12.0,
)
plt.show()
max_heapify
def max_heapify(A, i):
hs = len(A)
l = left(i)
r = right(i)
if l < hs and A[l] > A[i]:
largest = l
else:
largest = i
if r < hs and A[r] > A[largest]:
largest = r
if largest != i :
# show_tree(A)
A[i], A[largest] = A[largest], A[i]
max_heapify(A, largest)
build_max_heap
def build_max_heap(A):
for i in range(int(len(A)/2)-1, -1, -1):
# print(i)
max_heapify(A, i)
X = [4,1,3,2,16,9,10,14,8,7]
build_max_heap(X)
show_tree(X)
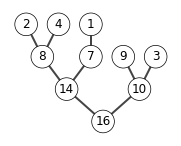
heap_sort
def heap_sort(A):
# print("build max heap")
build_max_heap(A)
# print("extracting elements from A")
hs = len(A)
B = []
for i in range(len(A) - 1, 0, -1):
B.append(A[0])
# print(B)
A = A[1:]
max_heapify(A, 0)
return B
X = [4,1,3,2,16,9,10,14,8,7]
print(heap_sort(X))
[16, 14, 10, 9, 8, 7, 4, 3, 2]
counting sort
def counting_sort(A):
INF = 0x7fffffff
n = len(A)
k = max(A)
C = [0 for i in range(k + 1)]
B = [0 for i in range(len(A))]
for j in range(n):
C[A[j]] += 1
for i in range(1, k + 1):
C[i] += C[i - 1]
for j in range(n - 1, -1, -1):
B[C[A[j]] - 1] = A[j]
C[A[j]] -= 1
return B
radix sort
def get_max_digit(A):
x = max(A)
i = 0
while x != 0:
x = int(x / 10)
i += 1
return i
def counting_sort_for_radix(A, Ad):
INF = 0x7fffffff
n = len(A)
k = max(A)
C = [0 for i in range(k + 1)]
B = [0 for i in range(len(A))]
for j in range(n):
C[Ad[j]] += 1
for i in range(1, k + 1):
C[i] += C[i - 1]
for j in range(n - 1, -1, -1):
B[C[Ad[j]] - 1] = A[j]
C[Ad[j]] -= 1
return B
def radix_sort(A, d):
# A = np.array(A)
for i in range(d):
B = [x // (10 ** i) for x in A]
B = [x % (10) for x in B]
print(B)
A = counting_sort_for_radix(A, B)
return A
A = [329, 457,89, 436, 63, 7]
d = get_max_digit(A)
radix_sort(A, d)
[9, 7, 9, 6, 3, 7]
[6, 3, 5, 0, 2, 8]
[0, 3, 4, 4, 0, 0]
[7, 63, 89, 329, 436, 457]
Heap
Heap and Heap Sort
6.1-2
Proof
A full binary tree with height \(k\) has
nodes.
If a heap has \(n\) nodes, then it satisfies
for some height \(k\). So \(k \leq \log n < k + 1\) i.e. \(k = \lfloor \log n \rfloor\).
!pip install igraph
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: igraph in /usr/local/lib/python3.7/dist-packages (0.10.1)
Requirement already satisfied: texttable>=1.6.2 in /usr/local/lib/python3.7/dist-packages (from igraph) (1.6.4)
import igraph as ig
import matplotlib.pyplot as plt
def left(i):
return 2 * (i + 1) - 1
def right(i):
return 2 * (i + 1)
def show_tree(X):
n_vertices = len(X)
edges = []
hs = len(X)
for i in range(int(len(X)/2) ):
if left(i) < hs:
edges.append((i, left(i)))
if right(i) < hs:
edges.append((i, right(i)))
Xs = [str(int) for int in X]
B = ["(" + str(i) + ")" + Xs[i] for i in range(len(X))]
g = ig.Graph(n_vertices, edges)
g.vs["name"] = X #!!!!
fig, ax = plt.subplots(figsize=(3,3))
layout = g.layout_reingold_tilford(root=[0])
ig.plot(
g,
target=ax,
layout=layout,
vertex_size=0.7,
vertex_color="white",
vertex_frame_width=0.7,
vertex_frame_color="black",
vertex_label=g.vs["name"],
vertex_label_size=12.0,
)
plt.show()
6.1-6
X = [23, 17, 14, 6, 13, 10 , 2, 5, 7, 12]
show_tree(X)
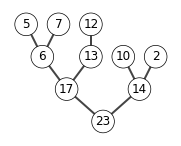
Since \(A[\operatorname{Parent}(i)] \geq A[i]\) for all \(i\) , this is a max-heap.
6.1-7
Proof First we show that node with index \(⌊\frac{n}{2} ⌋\) has at least one child. The index of node \(⌊\frac{n}{2} ⌋\)'s left child (if exist) is given by
\(2⌊\frac{n}{2} ⌋ = n\) if \(n\) is even and $2⌊\frac{n}{2} ⌋ = n -1 $ if \(n\) is odd. All circumstances are smaller then \(n\), so it has at least one child.
Then we show that \(⌊\frac{n}{2} ⌋ + k \quad (k\geq 1)\) has no child. Similar to the previous step, we have $2(⌊\frac{n}{2} ⌋ + k ) = n + 2k $ if \(n\) is even and $2(⌊\frac{n}{2} ⌋ + k ) = n -1 + 2k $ if \(n\) is odd, and all circumstances are all exceeding the maximum index. So they do not have childs.
Hence the index of leaves should starts by \(⌊\frac{n}{2} ⌋ + 1\) and ends by \(n\).
def max_heapify(A, i):
hs = len(A)
l = left(i)
r = right(i)
if l < hs and A[l] > A[i]:
largest = l
else:
largest = i
if r < hs and A[r] > A[largest]:
largest = r
if largest != i :
show_tree(A)
A[i], A[largest] = A[largest], A[i]
max_heapify(A, largest)
def build_max_heap(A):
for i in range(int(len(A)/2)-1, -1, -1):
# print(i)
max_heapify(A, i)
As = [str(int) for int in A]
print(As)
B = ["(" + str(i) + ")" + As[i] for i in range(len(A))]
print(B)
['15', '12', '9', '5', '6', '8', '7', '4', '0', '1', '2']
['(0)15', '(1)12', '(2)9', '(3)5', '(4)6', '(5)8', '(6)7', '(7)4', '(8)0', '(9)1', '(10)2']
6.2-1
X = [27,17,3,16,13,10,1,5,7,12,4,8,9,0]
show_tree(X)
max_heapify(X, 2)
show_tree(X)
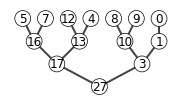
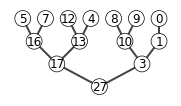
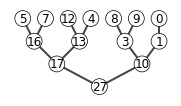
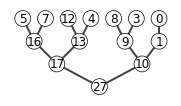
6.3-1
X = [5,3,17,10,84,19,6,22,9]
build_max_heap(X)
show_tree(X)
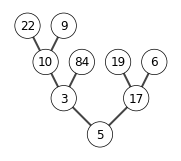
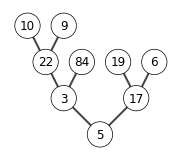
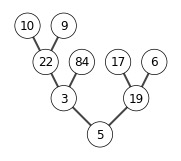
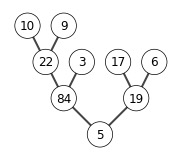
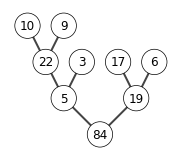
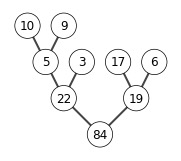
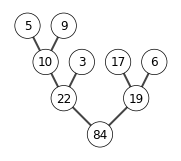
6.4-1
def heap_sort(A):
print("build max heap")
build_max_heap(A)
print("extracting elements from A")
hs = len(A)
B = []
for i in range(len(A) - 1, 0, -1):
B.append(A[0])
print(B)
A = A[1:]
max_heapify(A, 0)
return B
A = [5, 13, 2, 25, 7, 17, 20, 8,4]
B = heap_sort(A)
print(B)
build max heap
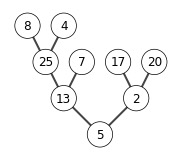
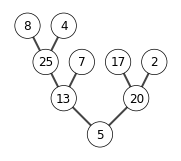
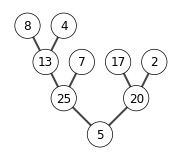
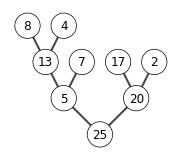
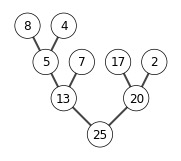
extracting elements from A
[25]
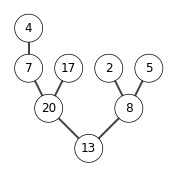
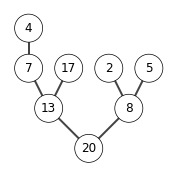
[25, 20]
[25, 20, 17]
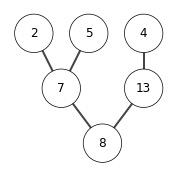
[25, 20, 17, 13]
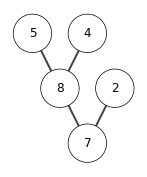
[25, 20, 17, 13, 8]
[25, 20, 17, 13, 8, 7]
[25, 20, 17, 13, 8, 7, 5]
[25, 20, 17, 13, 8, 7, 5, 4]
[25, 20, 17, 13, 8, 7, 5, 4]
Question
Prove that \(\lg 1+\lg 2+\cdots+\lg n \geq(n \lg n) / 2\).
Proof
Let \(k \leq n-1\), we have
therefore,
is smaller or equal than \(n!\) for \(1< k < n\).
Hence
def heap_max(A):
return A[0]
def heap_extract_max(A):
show_tree(A)
hs = len(A)
if hs < 1:
raise Exception("heap underflow")
max = A[0]
A[0] = A[hs - 1]
del A[0]
max_heapify(A, 0)
return max
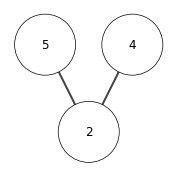
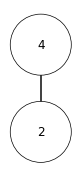
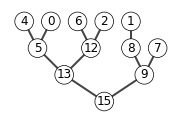
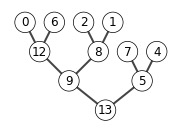
6.5-1
X = [15, 13, 9, 5, 12, 8, 7, 4,0,6,2,1]
# show_tree(X)
heap_extract_max(X)
show_tree(X)
def parent(i):
return int((i+1)/2)-1
def heap_increase_key(A, i, key):
if key < A[i]:
raise Exception("new key is smaller than current key")
A[i] = key
while i > 0 and A[parent(i)] < A[i]:
show_tree(A)
A[parent(i)], A[i] = A[i], A[parent(i)]
i = parent(i)
def max_heap_insert(A, key):
A.append(-0x7fffffff)
show_tree(A)
heap_increase_key(A, len(A) - 1, key)
6.5-2
A = [15, 13, 9, 5, 12, 8,7,4,0,6,2,1]
show_tree(A)
max_heap_insert(A, 10)
show_tree(A)
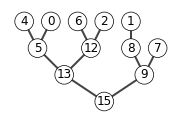
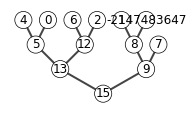
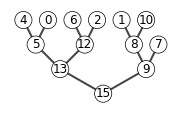
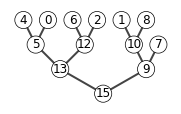
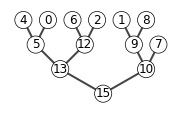
6.5-8
The code below is an implement of deleting an element in a heap.
def heap_delete(A, i):
hs = len(A)
A[i], A[hs - 1] = A[hs - 1], A[i]
del A[hs - 1]
max_heapify(A, i)
A = [15, 13, 9, 5, 12, 8,7,4,0,6,2,1]
show_tree(A)
heap_delete(A,1)
show_tree(A)
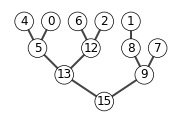
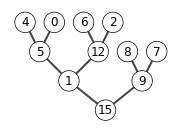
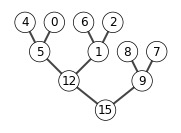
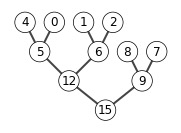
Sort in Linear Time
def counting_sort(A):
INF = 0x7fffffff
n = len(A)
k = max(A)
C = [0 for i in range(k + 1)]
B = [0 for i in range(len(A))]
for j in range(n):
C[A[j]] += 1
print("C:", end =" ")
print(C)
for i in range(1, k + 1):
C[i] += C[i - 1]
print("C:", end =" ")
print(C)
for j in range(n - 1, -1, -1):
B[C[A[j]] - 1] = A[j]
print("B:", end =" ")
print(B)
C[A[j]] -= 1
print("C:", end =" ")
print(C)
return B
import numpy as np
import random
# A = np.random.randint((10), size=10)
# A += 0
A = [5,0,2,0,1,3,2,5,1]
print(A)
print(counting_sort(A))
[5, 0, 2, 0, 1, 3, 2, 5, 1]
C: [0, 0, 0, 0, 0, 1]
C: [1, 0, 0, 0, 0, 1]
C: [1, 0, 1, 0, 0, 1]
C: [2, 0, 1, 0, 0, 1]
C: [2, 1, 1, 0, 0, 1]
C: [2, 1, 1, 1, 0, 1]
C: [2, 1, 2, 1, 0, 1]
C: [2, 1, 2, 1, 0, 2]
C: [2, 2, 2, 1, 0, 2]
C: [2, 4, 6, 7, 7, 9]
B: [0, 0, 0, 1, 0, 0, 0, 0, 0]
C: [2, 3, 6, 7, 7, 9]
B: [0, 0, 0, 1, 0, 0, 0, 0, 5]
C: [2, 3, 6, 7, 7, 8]
B: [0, 0, 0, 1, 0, 2, 0, 0, 5]
C: [2, 3, 5, 7, 7, 8]
B: [0, 0, 0, 1, 0, 2, 3, 0, 5]
C: [2, 3, 5, 6, 7, 8]
B: [0, 0, 1, 1, 0, 2, 3, 0, 5]
C: [2, 2, 5, 6, 7, 8]
B: [0, 0, 1, 1, 0, 2, 3, 0, 5]
C: [1, 2, 5, 6, 7, 8]
B: [0, 0, 1, 1, 2, 2, 3, 0, 5]
C: [1, 2, 4, 6, 7, 8]
B: [0, 0, 1, 1, 2, 2, 3, 0, 5]
C: [0, 2, 4, 6, 7, 8]
B: [0, 0, 1, 1, 2, 2, 3, 5, 5]
C: [0, 2, 4, 6, 7, 7]
[0, 0, 1, 1, 2, 2, 3, 5, 5]
Q: Is heap sort stable?
A: No. For example,
!pip install igraph
Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/
Requirement already satisfied: igraph in /usr/local/lib/python3.7/dist-packages (0.10.1)
Requirement already satisfied: texttable>=1.6.2 in /usr/local/lib/python3.7/dist-packages (from igraph) (1.6.4)
import igraph as ig
import matplotlib.pyplot as plt
def left(i):
return 2 * (i + 1) - 1
def right(i):
return 2 * (i + 1)
def show_tree(X):
n_vertices = len(X)
edges = []
hs = len(X)
for i in range(int(len(X)/2) ):
if left(i) < hs:
edges.append((i, left(i)))
if right(i) < hs:
edges.append((i, right(i)))
# Xs = [str(int) for int in X]
# B = ["(" + str(i) + ")" + Xs[i] for i in range(len(X))]
g = ig.Graph(n_vertices, edges)
g.vs["name"] = X
fig, ax = plt.subplots(figsize=(3,3))
layout = g.layout_reingold_tilford(root=[0])
ig.plot(
g,
target=ax,
layout=layout,
vertex_size=0.8,
vertex_color="white",
vertex_frame_width=0.7,
vertex_frame_color="black",
vertex_label=g.vs["name"],
vertex_label_size=12.0,
)
plt.show()
def max_heapify(A, i):
hs = len(A)
l = left(i)
r = right(i)
if l < hs and A[l] > A[i]:
largest = l
else:
largest = i
if r < hs and A[r] > A[largest]:
largest = r
if largest != i :
show_tree(A)
A[i], A[largest] = A[largest], A[i]
max_heapify(A, largest)
def build_max_heap(A):
for i in range(int(len(A)/2)-1, -1, -1):
# print(i)
max_heapify(A, i)
def heap_sort(A):
print("build max heap")
build_max_heap(A)
print("extracting elements from A")
hs = len(A)
B = []
for i in range(len(A) - 1, 0, -1):
B.append(A[0])
print(B)
show_tree(A)
A = A[1:]
max_heapify(A, 0)
return B
import numpy as np
A = [1,2,3,3,3,4,5]
B = [i for i in range(len(A))]
show_tree(A)
heap_sort(A)
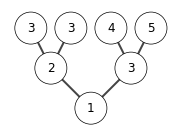
build max heap
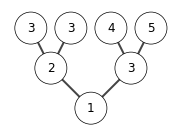
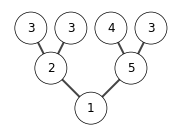
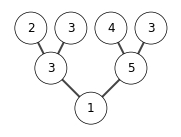
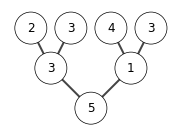
extracting elements from A
[5]
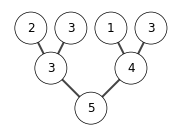
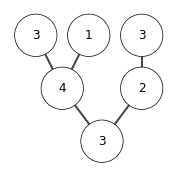
[5, 4]
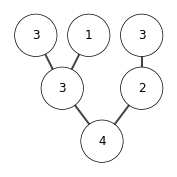
[5, 4, 3]
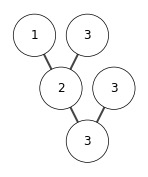
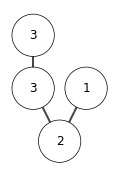
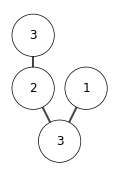
[5, 4, 3, 3]
[5, 4, 3, 3, 3]
[5, 4, 3, 3, 3, 2]
[5, 4, 3, 3, 3, 2]
in this example the nodes with same keys \(3\) has change its relative position during sort. So heap sort is not stable.
8.3-4
Show how to sort n integers in the range \(0\) to \(n^3 - 1\) in \(O(n)\) time.
Proof For linear sorting algorithms, we consider using Radix-Sort. First we use \(3\) digits \(n\)-base number to represent the input data, which can exactly represent \(n\) integers in the range \(0\) to \(n^3 - 1\). Since there are \(3\) dights, each digits with \(n\) numbers ranged \(n\), the total time complexity is \(\Theta \left( 3(n + n)\right) = \Theta (n)\)
Greedy Algorithm for Activity Selection Problem
class Activity:
def __init__(self, start, finish):
self.s = start
self.f = finish
def __lt__(self, other):
return self.f < other.f
def activity_selector(s, f):
n = len(s)
A = [1]
k = 1
for m in range(1, n):
if s[m] >= f[k]:
A = A + [m]
k = m
return A
def activity_selector_norank(s, f):
a = [Activity(s[i], f[i]) for i in range(len(s))]
a.sort()
n = len(s)
A = [1]
k = 1
for m in range(1, n):
if s[m] >= f[k]:
A = A + [m]
k = m
return A
s = [1,3,0,5,3,5,6,8,8,2,12]
f = [4,5,6,7,9,9,10,11,12,14,16]
A = activity_selector(s, f)
A1 = activity_selector_norank(s, f)
print(A)
print(A1)
[1, 3, 7, 10]
[1, 3, 7, 10]
Dijkstra’s Algorithm for Single-Source Shortest Path Problem
import numpy as np
INF = 0x7fffffff
def argmin_dijkstra(d, delta):
res = INF
res_ind_delta = 0
print(delta)
for i in range(len(delta)):
j = delta[i]
if res > d[j]:
res = d[j]
res_ind_delta = i
return res_ind_delta
def dijkstra(W, s):
n = len(W[0])
delta = [x for x in range(n)]
delta = np.array(delta)
d = [INF for x in range(n)]
d = np.array(d)
p = [-1 for x in range(n)]
d[s] = 0
p[s] = 0
while len(delta) > 0:
ind_of_delta_u = argmin_dijkstra(d, delta)
u = delta[ind_of_delta_u]
print("current u is")
print(u)
delta = np.delete(delta, ind_of_delta_u)
print("delta is")
print(delta)
print("d is")
print(d)
for v in range(n):
if W[u][v] >= INF or W[u][v] <= 0:
continue
if d[u] + W[u][v] < d[v]:
d[v] = d[u] + W[u][v]
p[v] = u
return d, p
n = 5
W = [[INF for x in range(n)] for x in range(n)]
W[0][1] = 10
W[0][2] = 3
W[1][3] = 2
W[1][2] = 1
W[2][1] = 4
W[2][4] = 2
W[2][3] = 8
W[3][4] = 7
W[4][3] = 9
for i in range(n):
W[i][i] = 0
s = 0
d, p = dijkstra(W, s)
d
[0 1 2 3 4]
current u is
0
delta is
[1 2 3 4]
d is
[ 0 2147483647 2147483647 2147483647 2147483647]
[1 2 3 4]
current u is
2
delta is
[1 3 4]
d is
[ 0 10 3 2147483647 2147483647]
[1 3 4]
current u is
4
delta is
[1 3]
d is
[ 0 7 3 11 5]
[1 3]
current u is
1
delta is
[3]
d is
[ 0 7 3 11 5]
[3]
current u is
3
delta is
[]
d is
[0 7 3 9 5]
array([0, 7, 3, 9, 5])
Prim’s Algorithm for Minimum Spanning Tree Problem
class Graph:
INF = 0x7fffffff
def __init__(self):
self.edge = list()
def add(self, u, v, w):
self.edge = self.edge + [(u, v, w)]
def print(self):
for i in self.edge:
print(i)
def get_vertex(self):
vertex = set()
for i in self.edge:
vertex.add(i[0])
vertex.add(i[1])
return vertex
def get_matrix_undirected(self):
vertex = self.get_vertex()
max_n = max(vertex)
g = [[self.INF for x in range(max_n + 1)] for x in range(max_n + 1)]
# print(g)
for i in self.edge:
u = i[0]
v = i[1]
w = i[2]
# print(u,v,w)
g[u][v] = w
g[v][u] = w
return g
# G = Graph()
# G.add(1,1,1)
# G.add(2,2,2)
# G.add(3,3,3)
# G.print()
# print(G.get_vertex())
# g = G.get_matrix_undirected()
# print(g)
# g[1][2]
def prim_min_spanning_tree(G):
n = max(G.get_vertex()) + 1
w = G.get_matrix_undirected()
vertex = G.get_vertex()
INF = 0x7fffffff
T = set()
s = [False for x in range(n)]
lowcost = [INF for x in range(n)]
closest = [-1 for x in range(n)]
ini_p = next(iter(vertex))
s[ini_p] = True
print(ini_p)
for i in range(0, n):
if i == ini_p:
continue
lowcost[i] = w[ini_p][i]
closest[i] = ini_p
s[i] = False
for i in range(0, n):
if i == ini_p:
continue
min_x = INF
j = ini_p
for k in range(0, n):
if k == ini_p:
continue
if lowcost[k] < min_x and not s[k]:
min_x = lowcost[k]
j = k
s[j] = True
print((closest[j],j))
print(lowcost)
if closest[j] != -1:
T.add((closest[j],j) )
for k in range(0, n):
if k == ini_p:
continue
if w[j][k] < lowcost[k] and not s[k]:
lowcost[k] = w[j][k]
closest[k] = j
return T
G = Graph()
G.add(1,2,6)
G.add(1,3,1)
G.add(1,4,5)
G.add(2,3,5)
G.add(2,5,3)
G.add(3,4,5)
G.add(3,5,6)
G.add(3,6,4)
G.add(4,6,2)
G.add(5,6,6)
w = G.get_matrix_undirected()
print(w)
T = prim_min_spanning_tree(G)
print(T)
[[2147483647, 2147483647, 2147483647, 2147483647, 2147483647, 2147483647, 2147483647], [2147483647, 2147483647, 6, 1, 5, 2147483647, 2147483647], [2147483647, 6, 2147483647, 5, 2147483647, 3, 2147483647], [2147483647, 1, 5, 2147483647, 5, 6, 4], [2147483647, 5, 2147483647, 5, 2147483647, 2147483647, 2], [2147483647, 2147483647, 3, 6, 2147483647, 2147483647, 6], [2147483647, 2147483647, 2147483647, 4, 2, 6, 2147483647]]
1
(1, 3)
[2147483647, 2147483647, 6, 1, 5, 2147483647, 2147483647]
(3, 6)
[2147483647, 2147483647, 5, 1, 5, 6, 4]
(6, 4)
[2147483647, 2147483647, 5, 1, 2, 6, 4]
(3, 2)
[2147483647, 2147483647, 5, 1, 2, 6, 4]
(2, 5)
[2147483647, 2147483647, 5, 1, 2, 3, 4]
(-1, 1)
[2147483647, 2147483647, 5, 1, 2, 3, 4]
{(6, 4), (3, 6), (3, 2), (2, 5), (1, 3)}