CINTA hw4-526互联

第七章
第八章

第七章

2.群 Z₁₇ * 有多少个生成元？已知 3 是其中一个生成元，请问 9 和 10 是否生成元？

Z_p* = { 1,2,3,…,16 }
|Z_p* |=16
Φ(16)=8,生成元8个
Z₁₇* 中与16互素的数有{1，3，5，7，9，11，13，15}
9=3² mod 17, 9不是生成元
10=3³mod 17, 10是生成元

3.p 和 q 是两个不同的素数，请问 Z_pq 都多少个生成元？r 是任意正整数，请问 Z_p^r都多少个生成元

对于群 Z_pq，φ(pq) = (p-1)(q-1)。
在 Z_pq 中，有 (p-1)(q-1) 个生成元。

对于群 Z_p^r，φ(p^r )= p^(r-1)(p-1) 。
则在 Z_p^r 中，有 p^(r-1)(p-1) 个生成元。

6.证明：如果群 G 没有非平凡子群，则群 G 是循环群。

证明：G有且仅有两个子群，{e}与平凡子群G，即本身。

{e}为循环群
∀g∈G且g≠e，< g >={g^k:k∈Z}为G的子群，< g >为由g生成的循环群
< g >＝G，故G为循环群。

8.证明：设 G 为任意群，且 g ∈ G。如果存在 m, n ∈ Z 使得 g^m = 1 且 gⁿ = 1，则g^d = 1，其中 d = gcd(m, n)。

证明：

g^m = 1 , gⁿ = 1
d = gcd(m, n)。
由 Bézout 定理，存在整数 x 和 y 使得 mx + ny = d。
g^d = g^{mx + ny}
= (g^m)^x · ( gⁿ )^y
= 1^x · 1^y
= 1
因此，g^d = 1，其中 d = gcd(m, n)。

第八章

1.证明：设 G 是群，H 是 G 的子群。任取 g₁, g₂ ∈ G，则 g₁H = g₂H 当且仅当 g₁^-1g₂ ∈ H。

g₁H = g₂H,证明 g1^-1g₂∈H 。

因为 g₁H = g₂H
所以对于 h ∈ H，有 g₁h = g₂。
等式两边同时左乘 g1^-1，得 g1^-1(g₁h) = g₁^-1g₂
有 h = g1^-1g₂ , h∈H
故g₁H = g₂H，有 g1^-1g₂∈H
g₁^-1g₂ ∈H，证明 g₁H = g₂H。

g₁^-1g₂ ∈ H，所以 g₁(g₁^-1g₂) ∈ g₁H。
有g₂ ∈ g₁H。
对于 h ∈ H，由上述证明，我们可以写成 h = g₁^-1g₂。
有 g₁h = g2，即 g₁(g₁^-1g₂) = g₂。
即g₂ ∈ g₁H。
故g₁^-1g₂∈ H，那么 g₁H = g₂H。

g₁H = g₂H当且仅当 g₁^-1g₂ ∈ H 得证。

3.如果 G 是群，H 是群 G 的子群，且 [G : H] = 2，请证明对任意的 g ∈ G，gH = Hg

证明：gH⊆Hg且Hg⊆gH
[G : H]=2，即H在G上有两个不同的左陪集。其中一个为H本身。
设另一个左陪集为H‘

由于 H 是 G 的子群，那么 e ∈ H，其中 e 是群 G 的单位元素。因此有 H = He。
H 和 gH 是 G 的左陪集，则 G = H ∪ gH。
若H∪ gH非空，那么由于H和 gH 是左陪集，它们的交集不应包含非空集合。
因此，H ∪ gH 必须是空集。
∃h∈H 使得 gh∈H。
即∀g ∈G，∃ h ∈H 使得 gh ∈ H，即 gH ⊆ H。
g ∈G，则 g = ge , e ∈ H。
H是子群，e ∈H，所以 g ∈ gH。
因此，H ⊆ gH。

综上所述， gH = Hg。

5.设 G 是阶为 pq 的群，其中 p 和 q 是素数。请证明 G 的任意非平凡子群是循环群

证明：
给定群 (G) 的阶为 (pq)，其中 (p) 和 (q) 是素数。现在我们来证明 (G) 的任意非平凡子群是循环群。

首先，由拉格朗日定理，|G| = pq，G可能的阶数为 1, p, q, pq。

|H| = 1，那么 H 是平凡子群。
|H| = p 或 |H| = q，
据拉格朗日定理， H 是 G 的一个非平凡的循环子群。
（p 和 q 是素数，所以只有平凡子群和 G 本身的阶才是 pq 的因数。）
|H| 只能为 p或 q。
|H| = pq，那么 H=G ，是非平凡的循环子群。

若|H| = p或 |H| = q 。
p 和 q 是素数，存在阶为 p 或 q 的循环群。
设|H| =p，是一个阶为 p 的子群。
由群论的基本定理，阶为 p的群同构于 C_p循环群。
同理， |H| = q，也同构于 C_q循环群。

对于任意非平凡子群 H，它都是循环群。

9.编程完成以下工作：对任意给定的一个素数 p，求出 Z_p* 的最小生成元。任取一个整数 n，对大于 1 小于 n 的所有素数 p，求 Z_p* 最小生成元，并求以上最小生成元集合中最大者所对应的素数 p。

点击查看代码

#include <iostream>
#include <cmath>
#include <vector>

bool isPrime(int n) {
    if (n < 2) {
        return false;
    }
    for (int i = 2; i <= sqrt(static_cast<double>(n)); i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

int gcd(int a, int b) {
    if (b == 0) {
        return a;
    }
    return gcd(b, a % b);
}

int findMinGenerator(int p) {
    std::vector<int> factors;
    int phi = p - 1;

    for (int i = 2; i <= sqrt(static_cast<double>(phi)); i++) {
        if (phi % i == 0) {
            factors.push_back(i);
            if (i != phi / i) {
                factors.push_back(phi / i);
            }
        }
    }

    for (int i = 2; i <= p; i++) {
        bool isGenerator = true;
        for (int factor : factors) {
            if (gcd(i, p) == 1 && static_cast<int>(pow(i, phi / factor)) % p == 1) {
                isGenerator = false;
                break;
            }
        }
        if (isGenerator) {
            return i;
        }
    }

    return -1;
}

int main() {
    int n;
    std::cout << "Enter a positive integer n: ";
    std::cin >> n;

    int maxGenerator = -1;
    int maxPrime = -1;

    for (int p = 2; p < n; p++) {
        if (isPrime(p)) {
            int generator = findMinGenerator(p);
            if (generator > maxGenerator) {
                maxGenerator = generator;
                maxPrime = p;
            }
        }
    }

    std::cout << "The maximum generator is " << maxGenerator << " for prime p = " << maxPrime << std::endl;

    return 0;
}

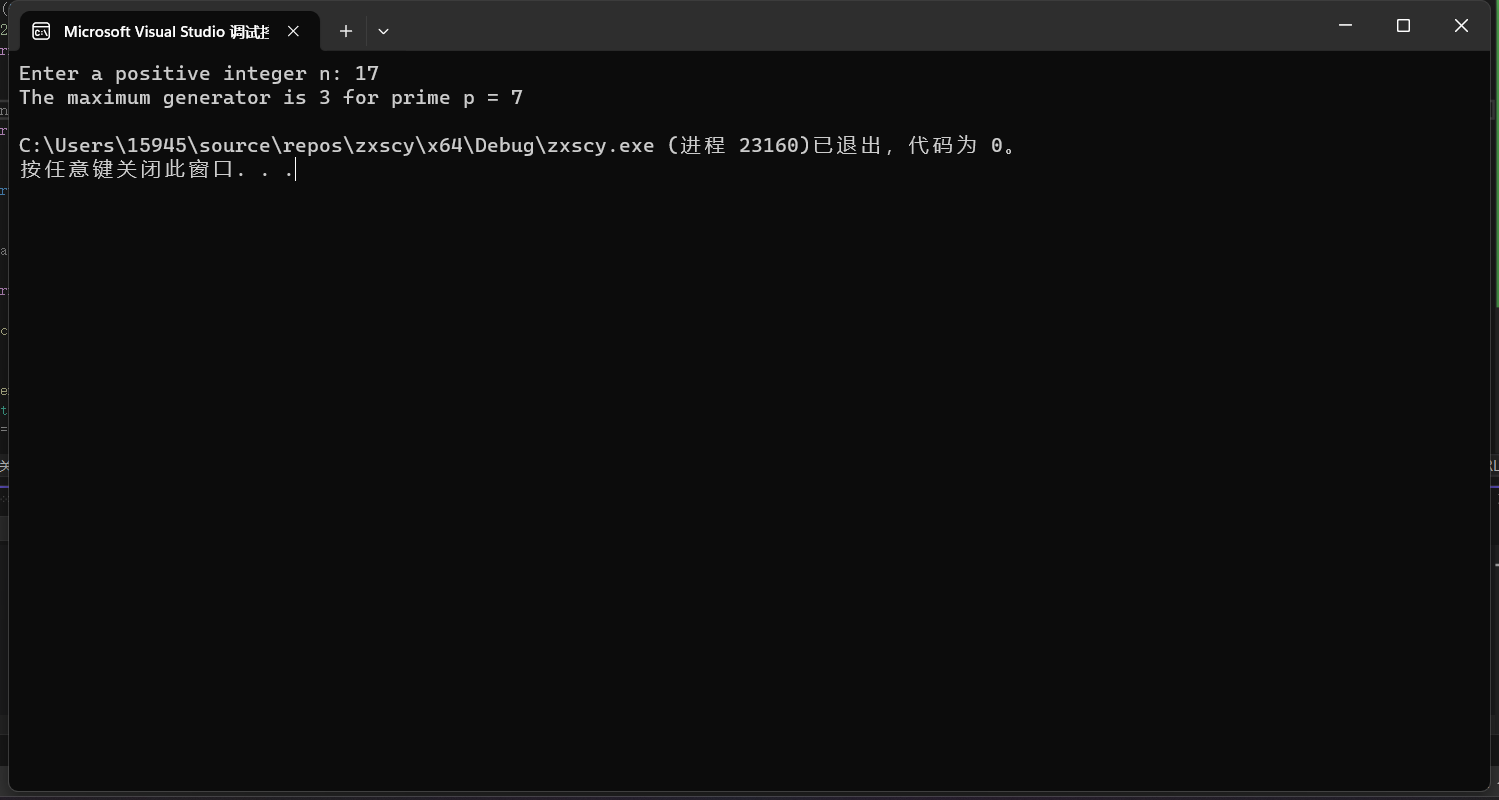
运行结果：