正交矩阵
正交:可以简单理解成就是垂直.
正交矩阵 定义:满足 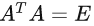 的矩阵.
的矩阵.


正交矩阵是指其转置等于逆的矩阵,性质是逆也是正交阵、积也是正交阵。
特征值、特征向量与变换是高等代数的灵魂,而正交变换是唯一没有发生形变的变换,由旋转和反射构成。
正交矩阵的定义“行向量和列向量皆为正交的单位向量”带来了另一个好处:正交矩阵的转置就是正交矩阵的逆,比普通矩阵求逆矩阵简单多了。
如果矩阵的各列向量都是单位向量,并且两两正交。那么就说这个矩阵是正交矩阵。(参考xyz三维空间, 各轴上一个长度为1的向量构成的矩阵)
对于正交矩阵,组成它的列向量 构成了一个空间的基,称之为:规范正交基。 而我们知道:对于一个空间而言,我们是可以找到很多个不同的基来表示的(参考相似矩阵的基底变换),那对于一个空间:假设已知的基底是非规范正交基,有什么办法获取到它的规范正交基呢?【施密特正交法】。
正交矩阵的几何意义
(https://www.cnblogs.com/yibeimingyue/p/16706756.html)
正交矩阵是方块矩阵,行向量和列向量皆为正交的单位向量。
行向量皆为正交的单位向量,任意两行正交就是两行点乘结果为0,而因为是单位向量,所以任意行点乘自己结果为1。
对于3x3正交矩阵,每行是一个3维向量,两个3维向量正交的几何意义就是这两个向量相互垂直。
所以3x3正交矩阵的三行可以理解为一个3D坐标系里的三个坐标轴,下面是3*3正交矩阵M,
x1, x2, x3, // x轴 y1, y2, y3, // y轴 z1, z2, z3,// z轴
单位矩阵表示的三个坐标轴就是笛卡尔坐标系里的x,y,z轴:
1, 0, 0, // x轴 0, 1, 0, // y轴 0, 0, 1, // z轴
一个向量乘以3x3正交矩阵的几何意义就是把这个向量从当前坐标系变换到这个矩阵所表示的坐标系里,比如下面的矩阵M1,
0, 1, 0, 1, 0, 0, 0, 0, 1,
一个向量(1, 2, 3)右乘这个矩阵M1得到新的向量(2, 1, 3),就是把原向量从原坐标系变换到一个新的坐标系。
新坐标系的x轴在原坐标系里是(0,1,0),即落在原坐标系的y轴上,
新坐标系就是把原坐标系的x和y轴对调,所以这个正交矩阵M1作用于向量(1,2,3)后把向量的x和y分量对调了。
正交矩阵:本身就是相互垂直,只是说它不见得是各个标准轴。以三维空间为例,我们希望正交矩阵是:

但是实际上他很可能是下边这个样子:
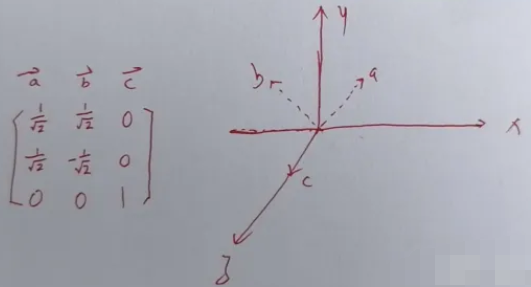
亦即以z轴为中心逆时针旋转了45°, 此时向量a,b,c依然相互正交,但是其列向量并不都在标准轴上.
而对角化的结果是一个对角矩阵,本质就是把矩阵列向量都放到标准轴上。 那么很显然:正交矩阵一定可以做到!
注意了,正交矩阵每个列向量都是单位向量,所以对角化后,按道理得到的是一个单位矩阵。
正交矩阵的性质
1、正交矩阵一定是对实矩阵而言的。
2、正交矩阵不一定对称。
3、正交矩阵的特征值为正负1或者cos(t)+isin(t),换句话说特征值的模长为1。
4、正交矩阵的行列式肯定是正负1,正1是叫第一类,负1时叫第二类。
5、对称的正交矩阵不一定是对角的,只是满足A'=A=A^{-1},例如副对角线全为1,其余元素都为零的那个方阵就是这种类型。
6、正交矩阵乘正交矩阵还是正交矩阵,但是正交矩阵相加相减不一定还是正交矩阵。
7、正交矩阵的每一个行(列)向量都是模为1的,并且任意两个行(列)向量是正交的,即所有的行(列)向量组成R^n的一组标准正交基。
8、正交矩阵每个元素绝对值都小于等于1,如果有一个元素为1,那么这个元素所在的行列的其余元素一定都为零。
9、一个对称矩阵,如果它的特征值都为1或者-1,那么这个矩阵一定是对称的正交矩阵。
10、如果b是一个n维单位实列向量,则E_n-2bb'是一个对称正交矩阵.因为E_n-2bb'的特征值为1(n-1重),-1(1重),同时还是一个对阵矩阵。
REF
https://zhuanlan.zhihu.com/p/258464098
https://jingyan.baidu.com/article/75ab0bcbafbd0497874db24f.html
https://zhuanlan.zhihu.com/p/258464098
https://baijiahao.baidu.com/s?id=1716565928303047882&wfr=spider&for=pc