本文主要是对顾樵老师 数物方法 一书对应章节的内容的梳理(主要为了抛砖引玉),有一些自己的理解,如有不妥,还请慷慨指出。
化简的理论
这里所说的二阶偏微分方程主要是指二阶线性双变量偏微分方程,它的一般形式如下所示:
\(A\frac{\partial^2u}{\partial x^2}+2B\frac{\partial^2 u}{\partial x\partial y}+C\frac{\partial^2 u}{\partial y^2}+D\frac{\partial u}{\partial y}+Fu = G\)
其中大写的英文字母都是\(x,y\)的函数,这是一个非齐次方程,如果\(G = 0\),那么它就变成一个齐次的方程。
为了化简上述方程,我们进行变量的替换: \(\xi = \xi(x,y);\ \eta = \eta(x,y)\). 需要注意的是这里进行变量替换的目的是为了化简上述方程,它可以用图表示为:
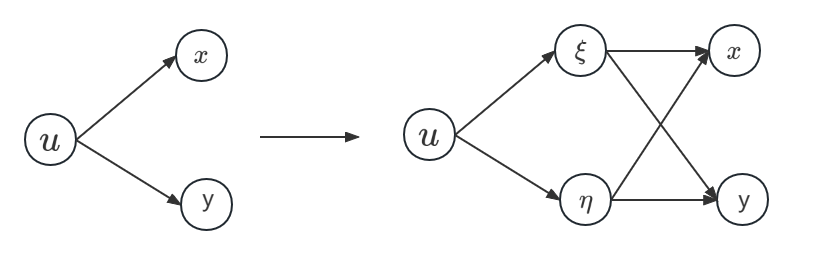
而在多元函数的微积分中我们也有过进行变量替换的操作(主要是为了进行积分的方便): \(x = x(\xi,\eta);\ y = y(\xi,\eta)\), 它的图为:

需要注意这两种变量替换是不同的,在多元函数的微积分中的变量替换一般是线性的,而这里为了化简方程所进行的变量替换一般不是线性的。
进行变量替换后的方程可以写为:
\(a\frac{\partial^2u}{\partial \xi^2}+2b\frac{\partial^2 u}{\partial \xi\partial \eta}+c\frac{\partial^2 u}{\partial \eta^2}+d\frac{\partial u}{\partial \eta}+fu = g\quad (1)\)
其中的小写字母如下所示:
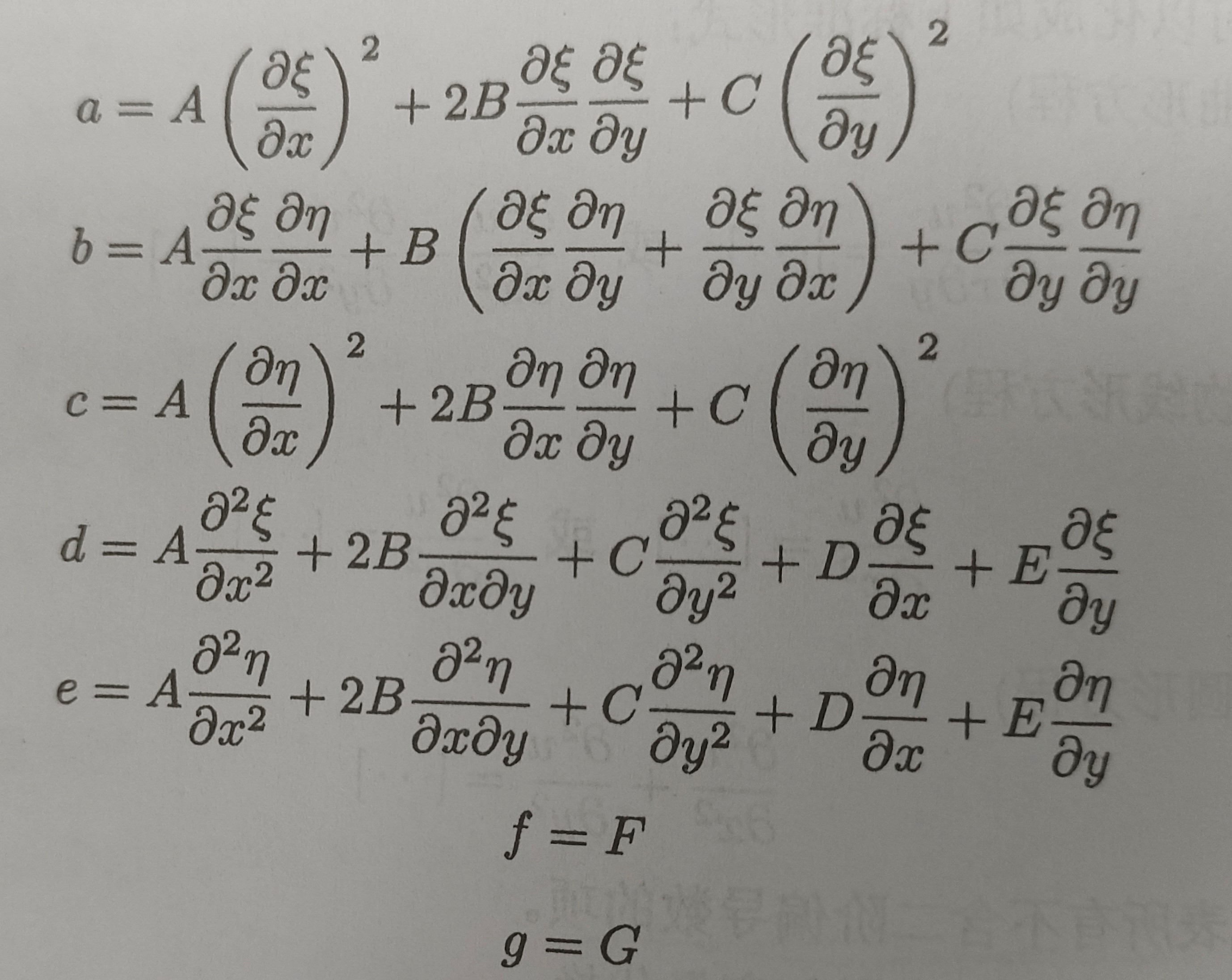
双曲型的: \(\frac{\partial^2 u}{\partial x\partial y} = 所有不含二阶偏导数的项\) 或者 \(\frac{\partial^2 u}{\partial x^2}-\frac{\partial^2 u}{\partial y^2} = 同前\)
抛物线型的: \(\frac{\partial^2 u}{\partial x^2} = 所有不含二阶偏导数的项\) 或者 \(\frac{\partial^2 u}{\partial y^2} = 同前\)
椭圆型的:\(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2} = 所有不含二阶偏导数的项\)
根据以上的想法,我们可以看到我们定义的变换\(\xi, \eta\)只需要使得(1)式中的二阶导数项中有一项或者两项的系数为0就可以达到目的。
这里\(a,c\)有相同的形式,我们先考虑它,进而考虑齐次方程
\(A(\frac{\partial W}{\partial x})^2+2B\frac{\partial W}{\partial x}\frac{\partial W}{\partial y}+C(\frac{\partial W}{\partial y})^2 = 0\quad (2)\)
当\(W\)不是常数时,两边同时除以\((\frac{\partial W}{\partial y})^2\), 可以得到下面的方程:
\(A(\frac{\frac{\partial W}{\partial x}}{\frac{\partial W}{\partial y}})^2+2B\frac{\frac{\partial W}{\partial x}}{\frac{\partial W}{\partial y}}+C = 0\)
此时,如果\(y = y(x)\),那么根据隐函数定理有\(\frac{dy}{dx} = -\frac{\frac{\partial W}{\partial x}}{\frac{\partial W}{\partial y}}\)
那么有:
\(A(\frac{dy}{dx})^2-2B(\frac{dy}{dx})+C = 0\)
这是一个关于\(y'\)的二次方程,它的解为:
\(y' = \frac{B+\sqrt{B^2-AC}}{A}\) 以及 \(y' = \frac{B-\sqrt{B^2-AC}}{A}\)
那么根据\(\Delta = B^2-AC\)的情况我们有:
a. \(\Delta \gt 0\)时,有两个不同的\(\frac{dy}{dx}\),从而解出两个不同的\(y_1 = y_1(x)\) 和 \(y_2 = y_2(x)\), 那么通过整理可以得到\(\xi(x,y_1) = \gamma_1\)以及\(\eta(x,y_2) = \gamma_2\)
其中\(\gamma_1\)和\(\gamma_2\)是任意的两个常数,它们的存在保证了\(\xi(x,y_1)\)和\(\eta(x,y_2)\)使得\(a = c = 0\), 从而达到将(1)式化简为双曲型的目的。
b. \(\Delta = 0\)时,有两个相同的\(\frac{dy}{dx}\), 从而解出一种 \(y = y(x)\), 整理得到\(\xi(x,y) = \gamma_1\)这里 \(\gamma_1\)的存在使得\(a = 0\)(当然也可以是\(c= 0\), 但是它俩只有一个等于0)。另外,将\(B^2 = AC\)带入上面求\(b\)的式子中我们可以得到\(b = 0\), 结合\(a = 0\), 我们可以将(1)式化简为抛物线型的式子。
c. \(\Delta \lt 0\)时,\(\frac{dy}{dx}\)有一对共轭复函数解,从而解出一对共轭的复函数\(y_1 = y_1(x)\)以及\(y_2 = y_2(x)\)。这里假设得到的其中一个整理过后的复函数解为\(\psi(x,y) = \psi_1(x,y)+i\psi_2(x,y)\), 这里\(\psi(x,y)\)满足方程(2),即\(A(\frac{\partial \psi}{\partial x})^2+2B\frac{\partial \psi}{\partial x}\frac{\partial \psi}{\partial y}+C(\frac{\partial \psi}{\partial y})^2 = 0\) , 根据这个等式,把\(\psi\)换为\(\psi_1+i\psi_2\)然后进行化简,最后根据实部和虚部都为0,可以得到下列方程:
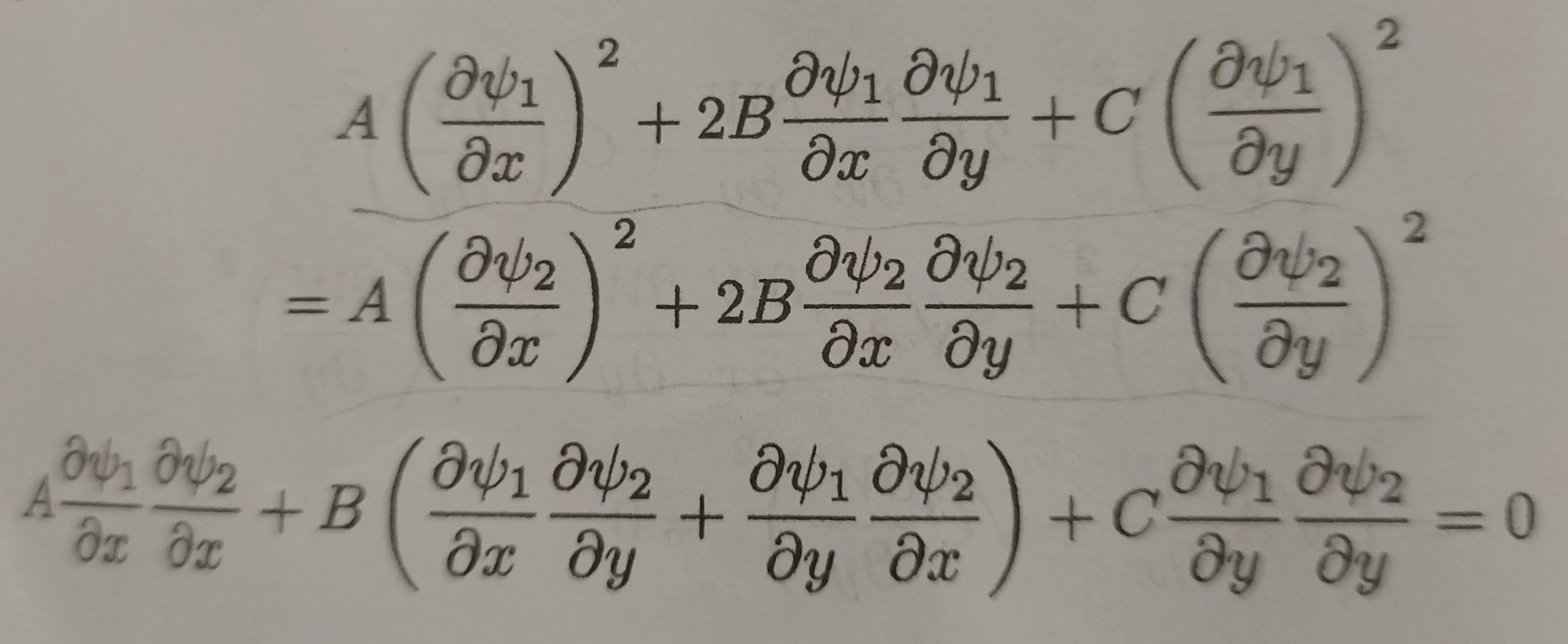
这个方程结合前面\(a,b,c\)的方程可以得出,如果取\(\xi = \psi_1(x,y)\), \(\eta = \psi_2(x,y)\), 那么有\(a = c\),\(b = 0\),那么方程(1)就可以化简为椭圆型的方程。
化简的步骤
根据上面介绍的化简的理论,下面我们来总结一下给定一个二阶线性双变量的偏微分方程,我们如何对其进行化简:
①. 首先识别出给定的二阶偏微分方程中对应上面的\(A,B,C\),然后计算出\(\Delta\)
②. 根据计算出的\(\Delta\)求解出\(y = y(x)\), 然后整理成为\(\xi(x,y) = \gamma_1\)和\(\eta(x,y) = \gamma_2\)
③. 利用②中的结果求解出其他系数(\(b,d,e\)),最后带入到变换后的方程(1)中得到结果。