微分中值定理
一、罗尔定理
内容
如果函数 \(f(x)\) 满足:
- 在 \([a,b]\) 上连续;
- 在 \((a,b)\) 内可导;
- 在区间端点处的函数值相等,即 \(f(a)=f(b)\)。
那么在 \((a,b)\) 内至少有一点 \(\xi(a<\xi<b)\) 使得函数 \(f(x)\) 在该点处的导数零,即 \(f'(\xi)=0\)。
证明
由于函数 \(f(x)\) 在 \([a,b]\) 上连续,有闭区间上连续函数最值定理可知,\(f(x)\) 在 \([a,b]\) 上必定取得最大值 \(M\) 和最小值 \(m\)。
当 \(M=m\) 时,\(f(x)\) 在 \([a,b]\) 上必为常数:\(y\equiv M\),于是 \(f'(x)\equiv 0\)
因此任取一点 \(\xi\in (a,b)\),都有 \(f'(\xi)=0\)。
当 \(M>m\) 时,\(M\) 和 \(m\) 这两个数中至少有一个不等于 \(f(a)\)。
不妨设 \(M \ne f(a)\),由于 \(f(a)=f(b)\),因此 \(M\ne f(b)\)。
于是存在 \(\xi\in (a,b)\),使得 \(f'(\xi)=M\)。
因此对 \([a,b]\) 上的任意 \(x\),有 \(f(\xi)\ge f(x)\),从而由费马定理可知 \(f'(\xi)=0\)。
证毕。
几何意义
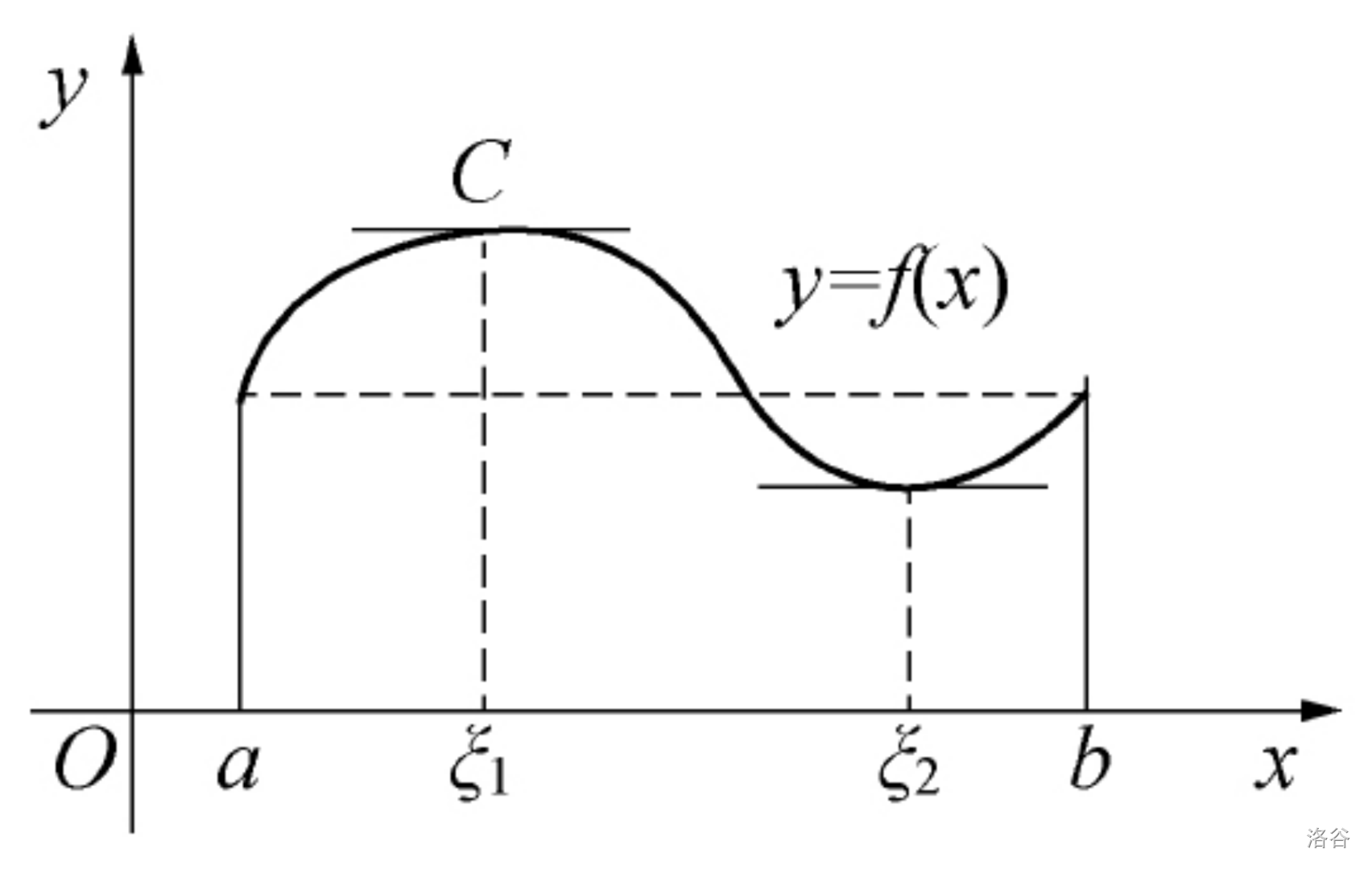
如果曲线段 \(f(x)(x\in[a,b])\) 是连续不断的、光滑的,且两端纵坐标相等,则该曲线段在 \([a,b]\) 上至少有一条水平切线。
二、拉格朗日中值定理
内容
如果函数 \(f(x)\) 满足:
- 在 \([a,b]\) 上连续;
- 在 \((a,b)\) 内可导;
那么在 \((a,b)\) 内至少有一点 \(\xi(a<\xi<b)\) 使得 \(f'(\xi)=\frac{f(b)-f(a)}{b-a}\), 即 \(f(b)-f(a)=f(\xi)(b-a)\)。
证明
令 \(g(x)=f(x)-\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)-f(a)\)。
如图所示,\(g(x)\) 即为曲线 \(f(x)\) 与直线 \(f(a)+\displaystyle\frac{f(b)-f(a)}{b-a}(x-a)\) 的纵坐标之差。
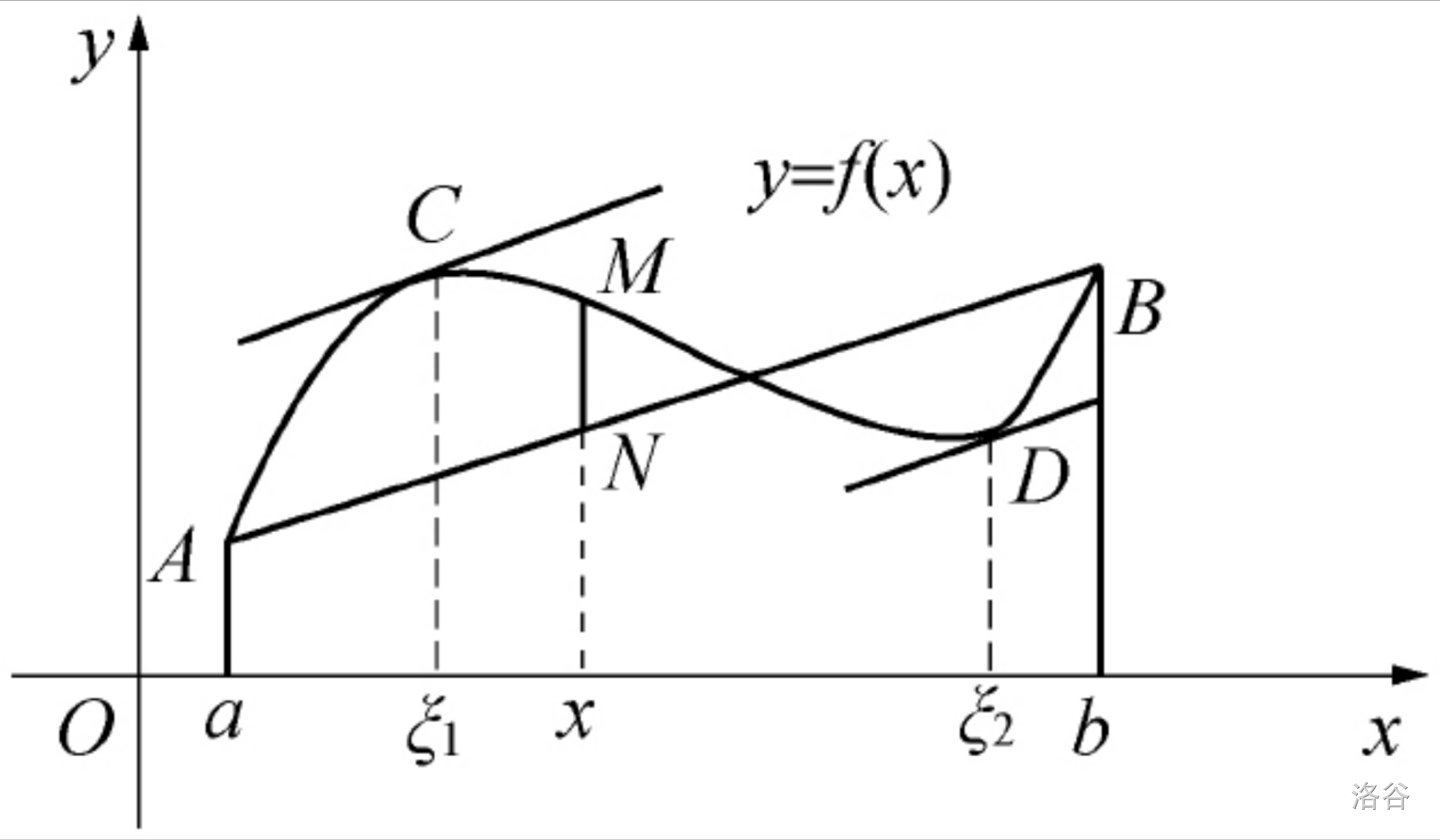
\(g(x)\) 在 \([a,b]\) 上连续,在 \((a,b)\) 内可导,且 $f(a)=f(b)=0 $。
则由罗尔定理知至少有一点 \(\xi(a<\xi<b)\) 使得函数 \(f(x)\) 在该点处的导数零。
即 \(f'(\xi)=0\),即 \(f'(\xi)=\displaystyle\frac{f(b)-f(a)}{b-a}\)。
证毕。
几何意义
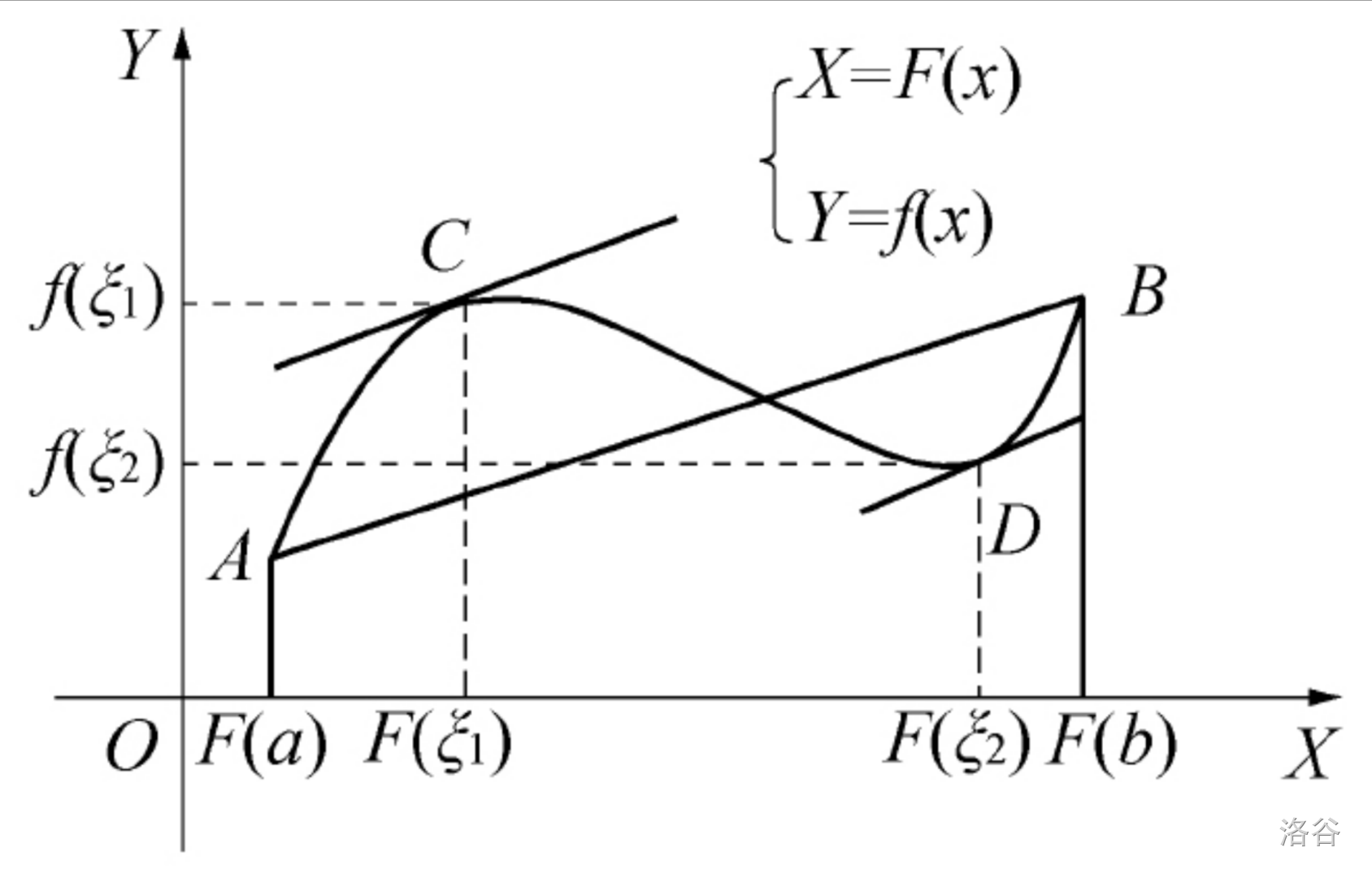
如果曲线段 \(f(x)(x\in[a,b])\) 是连续不断的、光滑的,且除端点外处处具有不垂直于横坐标轴的切线,则该曲线段在 \([a,b]\) 上至少有一点,使曲线在该点处的切线与两端点的连线(弦)平行。

柯西中值定理
内容
如果函数 \(f(x)\),\(g(x)\) 满足:
- 在 \([a,b]\) 上连续;
- 在 \((a,b)\) 内可导;
- 当 \(x\in(a,b) 时,g'(x)\ne 0\)。
则至少存在一点 \(\xi\in(a,b)\) 使得:
证明
可构造辅助函数:
其中 \(h(x)\) 在 \([a,b]\) 上连续,在 \((a,b)\) 内可导,且有 \(g(a)=g(b)=0\)。
由罗尔定理可知 \(\exist\xi\in(a,b)\) 使得 \(g'(\xi)=0\),即 :
又 \(g'(x)\ne 0\),所以有:
证毕。