526互联

三维计算几何

发布时间 2023-11-26 10:30:58作者: Martian148

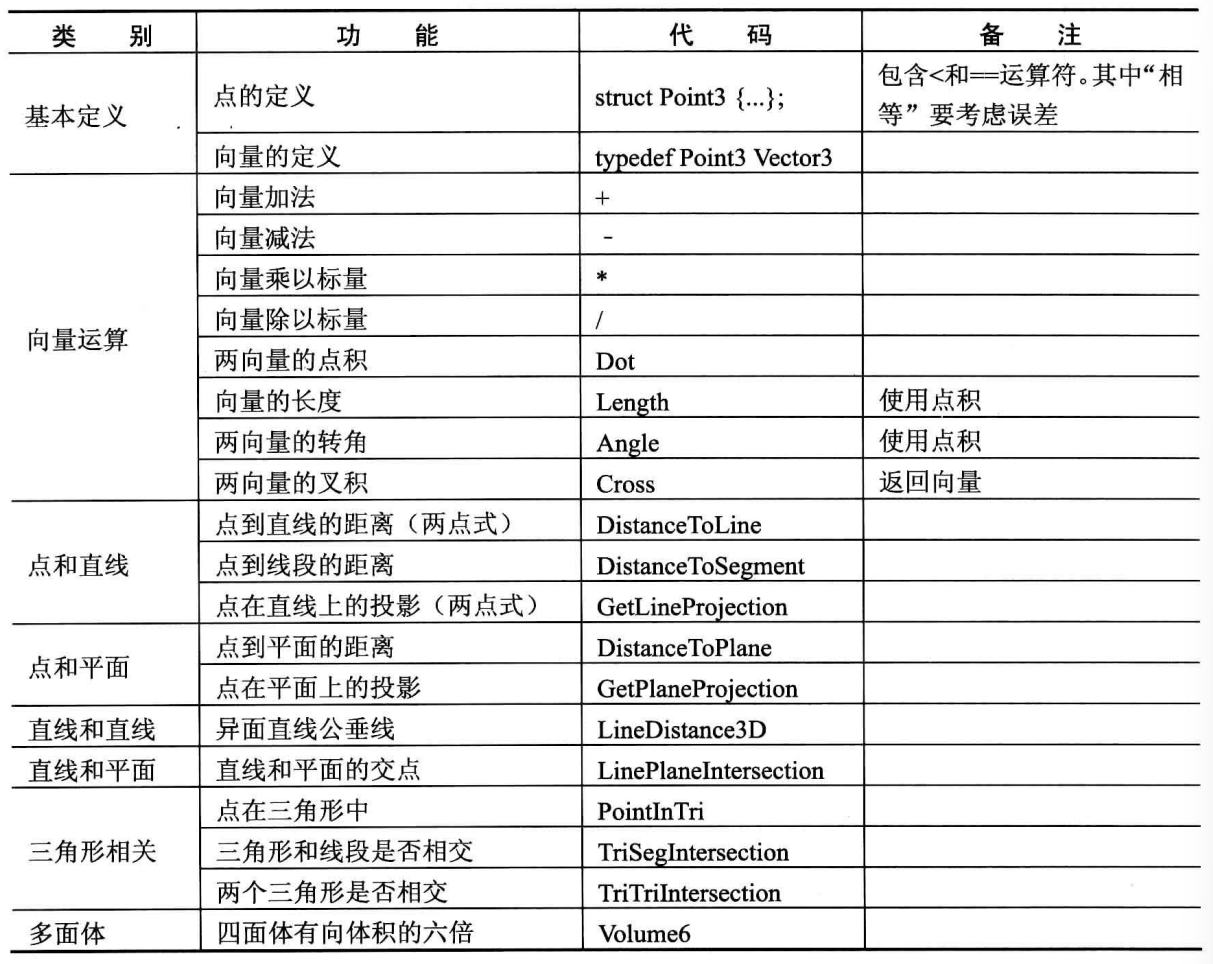
定义

struct Point3{
    double x,y,z;
    Point3(double x=0,double y=0,double z=0):x(x),y(y),z(z){}
};
typedef Point3 Vector3;

基本运算

Vector3 operator +(Vector3 A,Vector3 B){return Vector3(A.x+B.x,A.y+B.y,A.z+B.z);}
Vector3 operator -(Point3 A,Point3 B){return Vector3(A.x-B.x,A.y-B.y,A.z-B.z);}
Vector3 operator *(Vector3 A,double p){return Vector3(A.x*p,A.y*p,A.z*p);}
Vector3 operator /(Vector3 A,double p){return Vector3(A.x/p,A.y/p,A.z/p);}

直线的表示，可以用参数方程 （点和向量）来表示，射线和线段可以看成”参数由取值范围限制的“的直线

平面的表示，用点法式 \((p_0,n)\)， 其中 \(p_0\) 是平面上的一个点，向量 \(n\) 是平面的法向量。每个平面把空间分成了两个部分，我们用点法式表示其中一个半空间，是法向量所背离的哪一个。\(n\) 垂直于平面上的所有直线。平面上任意点 \(p\) 满足 \(Dot(n,p-p_0)=0\) 。设 \(p\) 的坐标为 \((x,y,z)\) ，\(p_0\) 的坐标为 \((x_0,y_0,z_0)\) ，向量 \(n\) 的坐标表示为 \((A,B,C)\) 上述等式等价于 $$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$$
整理得： \(Ax+By+Cz-(Ax_0+By_0+Cz_0)=0\) 如果令 \(-(Ax_0+By_0+Cz_0)\)，就得到了平面的一般式 $$Ax+By+Cz+D=0$$
当 \(Ax+By+Cz+D>0\) 上述点积大于 \(0\) ，即点 \((x,y,z)\) 在半平面空间 \((p_0,n)\) 外。换句话说 \(Ax+By+Cz+D>0\) 表示的是以一个半空间

点积

double Dot(Vector3 A,Vector3 B) {return A.x*B.x+A.y*B.y+A.z*B.z;}

长度

double Length(Vector3 A) {return sqrt(Dot(A,A));}

向量夹角

double Angle(Vector3 A,Vector3 B) {return acos(Dot(A,B)/Length(A)/Length(B));}

点到平面的距离

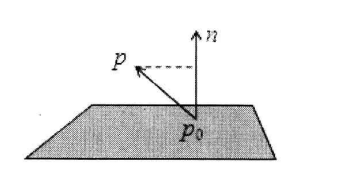
image.png

把 \(p-p_0\) 投影到向量 \(n\) 上可得 ：\(p\) 到平面的有向距离为 \(Dot(p-p_0,n)/Length(n)\)。

double DistanceToPlane(Point3 p,Point3 p0,Vector3 n){return fabs(Dot(p-p0,n))/Length(n);}//点 p 到平面 p0-n 的距离，如果不取绝对值，得到的是有向距离

点在平面上的投影点

设 \(p\) 在平面 \((p_0,n)\) 上的投影为 \(p'\) 则 \(p'-p\) 平行于 \(n\) ，且 \(p'-p=dn\) 其中 \(d\) 为 \(p\) 到平面的的有向距离

Point3 GetPlaneProjection(Point3 p,Point3 p0,Vector3 n){//点在平面上的投影
    double d=Dot(p-p0,n)/Length(n);
    return p-n*d;
}

直线和平面的交点

设平面方程为 \(\operatorname{Dot}(n,p-p_0)=0\)，过点 \(p_1\) 和 \(p_2\) 的直线的参数方程为 \(p=p_1+t(p_2-p_1)\) ，则与平面方程联立解得$$t=\operatorname{Dot}(n,p_0-p_1)/\operatorname{Dot}(n,p_2-p_1)$$
如果分母为 \(0\) 则直线和平面平行，或者直线在平面上

如果平面用一般式 \(Ax+By+Cz+D=0\) ，则联立出来的表达式为

\[t=\frac{Ax_1+By_1+Cz_1+D}{A(x_1-x_2)+B(y_1-y_2)+C(z_1-z_2)} \]

叉积

三维叉积的结果是一个向量

\[v_1 \times v_2=\begin{bmatrix}y_1z_2-y_2z_1\\z_1x_2-z_2x_1\\x_1y_2-x_2y_1\end{bmatrix} \]

叉积同时垂直于 \(v_1\) 和 \(v_2\) ，方向遵循右手定则。当且仅当 \(v_1\) 和 \(v_2\) 平行时，叉积为 \(0\)

Vector3 Cross(Vector3 A, Vector3 B) {return Vector3(A.y*B.z-A.z*B.y,A.z*B.x-A.x*B.z,A.x*B.y-A.y*B.x);}

通过向量叉积，可以进行一些拓展的基础问题。

过不共线的三点的平面，法向量为 \(\operatorname{Cross}(p_2-p_0,p_1-p_0)\) ，任取一个点即可得到平面的点法式。

三角形的有向面积的两倍

double Area2(Point3 A,Point3 B,Point3 C) {return Length(Cross(B-A,C-A));}

判断点是否在三角形内

先判断点是否在三角形所在平面上，然后利用简单的面积关系即可

bool TriSegIntersection(Point3 P0,Point3 P1,Point3 P2,Point3 A,Point3 B,Point3& P){//▲P0P1P2是否和线段AB相交
    Vector3 n=Cross(P1-P0,P2-P0);
    if(dcmp(Dot(n,B-A))==0) return false; //线段 AB 和平面 P0P1P2 平行或共面
    else{
        double t=Dot(n,P0-A)/Dot(n,B-A);
        if(dcmp(t)<0||dcmp(t-1)>0) return false; //交点不在线段AB上
        P=A+(B-A)*t;  //计算交点
        return PointInTri(P,P0,P1,P2);  //判断交点是否在三角形 P0-P1-P2 内
    }
}

点到直线/线段的距离，用面积法

double DistanceToLine(Point3 P,Point A,Point3 B){
    Vector3 v1=B-A,V2=P-A;
    return Length(Cross(v1,v2))/Length(v1);
}

四面体的体积

已知 \(4\) 个顶点为 \(A,B,C,D\)

\[V=\frac{1}{3}S\cdot h = \frac{1}{6}(\overrightarrow{AB}\times \overrightarrow{AC})\cdot h=\frac{1}{6}(\overrightarrow{AB}\times \overrightarrow{AC})\cdot \overrightarrow{AD} \]

三维凸包

求三位凸包的求法有很多，常用的有暴力法，卷包裹法，和增量法。

初始时随机选取两个点 \(p_1,p_2\) 然后找一个不和两个点共线的点 \(p_3\) 找一个和他们不共面的点 \(p_4\) 组成初始凸包。 然后依次考虑其他店 \(p_r\)

  • 如果这个点在当前的凸包内，直接忽略
  • 否则找到这个点能 "看到" 的所有面，删除他们，然后把阴影边界上的所有点和 \(p_r\) 连接起来，其中每条边和 \(p_r\) 一起构成一个三角形

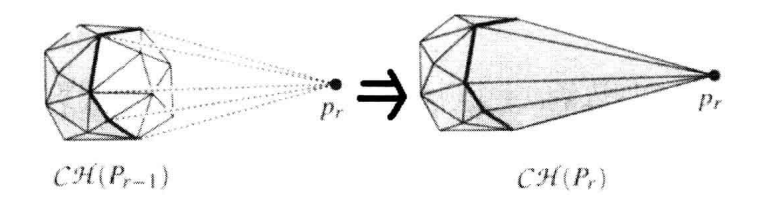
image.png

实现方法就是遍历所有面，判断是否可见，然后遍历所有边，判断是否在阴影边界上（即该边的两侧恰好有一个面可见）。

struct Face{
    int v[3]; //v表示三个点的序号
    Vector3 normal(Point3 *P) const{return Cross(P[v[1]]-P[v[0]],P[v[2]]-P[v[0]]);}
    int cansee(Point3 *P,int i) const{return Dot(P[i]-P[v[0]],normal(P))>0?1:0;} //i能不能看到P这个平面
};

vector<Face> CH3D(Point3 *P,int n){
    vector<Face> cur; //cur表示现在选中在凸包里面的面、
    cur.push_back((Face){{0,1,2}});
    cur.push_back((Face){{2,1,0}});
    for(int i=3;i<n;i++){
        vector<Face> next;
        for(int j=0;j<cur.size();j++){
            Face& f=cur[j];
            int res=f.cansee(P,i);
            if(!res) next.push_back(f); //如果不能看见，则不管
            for(int k=0;k<3;k++) //如果能看见，把这个面的每一条边标记
                vis[f.v[k]][f.v[(k+1)%3]]=res;
        }
        for(int j=0;j<cur.size();j++)
            for(int k=0;k<3;k++){
                int a=cur[j].v[k],b=cur[k].v[(k+1)%3];
                if(vis[a][b]!=vis[b][a]&&vis[a][b])  //如果一个边，只有相邻的一个平面被标记，那么这个边就被选中
                    next.push_back((Face){{a,b,i}});
            }
        cur=next;
    }
    return cur;
}

如果存在凸包上多点共面，简单起见，实践中常常把输入点进行微笑扰动后在调用上述过程

double rand01() {return rand()/(double)RAND_MAX;}  
double randeps() {return (rand01()-0.5)*eps;} //-eps/2到eps/2的随机数
Point3 add_noise(Point3 p){return Point3(p.x+randeps(),p.y+randeps(),p.z+randeps());}

扰动之前的点需要备份。上述代码记录的是 \(Face\) 是顶点的下标，所以可以用扰动后的点求三维图包，然后用这些下标引用原来 (未扰动的点)。此外，输入点应该先判重，否则在扰动后容易出现极小的面，这样的面容易造成麻烦。

三维向量小结

image.png