526互联

二维几何

发布时间 2023-11-17 00:16:34作者: Martian148

定义向量

struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){};
};

typedef Point Vector;

Vector operator + (Vector A,Vector B) {return Vector{A.x+B.x,A.y+B.y};} //向量+向量=向量
Vector operator - (Point A,Point B) {return Vector{A.x-B.x,A.y-B.y};} //点-点=向量
Vector operator * (Vector A,double p) {return Vector{A.x*p,A.y*p};} //向量*数=向量
Vector operator / (Vector A,double p) {return Vector{A.x/p,A.y/p};} //向量/数=向量

bool operator<(const Point& a,const Point& b){
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}

const double eps=1e-9;
int dcmp(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;}
bool operator ==(const Point &a,const Point &b){
    return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}

基本运算

点积

\(\overrightarrow{OA} \cdot \overrightarrow{OB}=x_Ax_B+y_Ay_B\)

double Dot(Vector A,Vector B) {return A.x*B.x+A.y*B.y;}
double Length(Vector A) {return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B) {return acos(Dot(A,B)/Length(A)/Length(B));}

叉积

\(\overrightarrow{OA} \times \overrightarrow{OB}=x_Ay_B+x_By_A\)

double Cross(Vector A,Vector B) {return A.x*B.y-A.y*B.x;}
double Area2(Point A,Point B,Point C) {return Cross(B-A,C-A);}

向量旋转

\(x'=x \cos a - y \sin a,y'=x \sin a+y \cos a\)

\[\begin{bmatrix}x'\\y'\end{bmatrix}= \begin{bmatrix}\cos x &\ -sinx\\\sin x\ &\ cos x\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix} \]

//向量逆时针旋转 rad
Vector Rotate(Vector A,double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));} //rad是弧度

求单位法向量

//求向量的单位法线,调用前判断 A 是不是零向量
Vector Normal(Vector A){double L=Length(A);return Vector(-A.y/L,A.x/L);}

完整代码

struct Point{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){};
};

typedef Point Vector;

Vector operator + (Vector A,Vector B) {return Vector{A.x+B.x,A.y+B.y};} //向量+向量=向量
Vector operator - (Point A,Point B) {return Vector{A.x-B.x,A.y-B.y};} //点-点=向量
Vector operator * (Vector A,double p) {return Vector{A.x*p,A.y*p};} //向量*数=向量
Vector operator / (Vector A,double p) {return Vector{A.x/p,A.y/p};} //向量/数=向量

bool operator<(const Point& a,const Point& b){
    return a.x<b.x||(a.x==b.x&&a.y<b.y);
}

const double eps=1e-9;
int dcmp(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;}
bool operator ==(const Point &a,const Point &b){
    return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}

double Dot(Vector A,Vector B) {return A.x*B.x+A.y*B.y;}
double Length(Vector A) {return sqrt(Dot(A,A));}
double Angle(Vector A,Vector B) {return acos(Dot(A,B)/Length(A)/Length(B));}

double Cross(Vector A,Vector B) {return A.x*B.y-A.y*B.x;}
double Area2(Point A,Point B,Point C) {return Cross(B-A,C-A);}

//向量逆时针旋转 rad
Vector Rotate(Vector A,double rad){return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));} //rad是弧度

//求向量的单位法线,调用前判断 A 是不是零向量
Vector Normal(Vector A){double L=Length(A);return Vector(-A.y/L,A.x/L);}

点和直线

直线可以用直线上一点 \(P_0\) 和方向向量 \(v\) 表示(虽然这个向量的大小没什么用处)。直线上所有点 \(P\) 满足 \(P=P_0+tv\) 其中 \(t\) 称为参数。如果已知直线上的两个不同点 \(A,B\) 则方向向量为 \(B-A\) 所以参数方程为 \(A+(B-A)t\)

参数方程方便的地方在于直线，射线和线段的方程形式是一样的，区别仅仅在于参数。直线的 \(t\) 没有范围限制，涉嫌的 \(t>0\) 线段的 \(t\) 在 \(0 \sim 1\) 之间，这样很多对于直线使用的公式可以很方便的用在射线和线段上

直线交点

设直线分别为 \(P+tv\) 和 \(Q+tw\) ，设向量 \(\overrightarrow{u}=QP\) ，交点在第一条直线的参数为 \(t_1\)，第二条直线上的参数为 \(t_2\) 则 \(x\) 和 \(y\) 坐标可以列出一个方程，解得

\[t_1=\frac{cross(w,u)}{cross(v,w)},t_2=\frac{cross(v,u)}{cross(v,w)} \]

代码如下，调用前请确保两条直线有唯一交点，当且仅当 \(Cross(v,w) \ne 0\)

Point GetLineInersection(Point P,Vector v,Point Q,Vector w){
    Vector u=P-Q;
    double t=Cross(w,u)/Cross(v,w);
    return P+v*t;
}

点到直线的距离

用叉积算出，用平行四边形的面积除以底

double DistanceToLine(Point P,Point A,Point B){
    Vector v1=B-A,v2=P-A;
    return fabs(Cross(v1,v2))/Length(v1);
}

点到线段的距离

点到线段的距离有两种可能

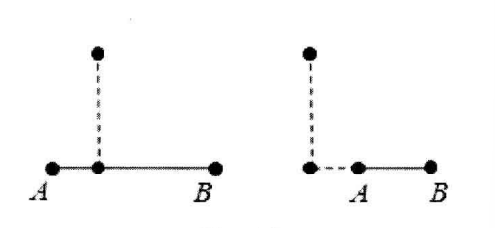
image.png

如果投影点为 \(Q\) 如果 \(Q\) 在线段 \(AB\) 上，则所求距离就是 \(P\) 点直线 \(AB\) 的距离(左图)，如果在射线 \(BA\) 上，则所求距离为 \(QA\) ，如果在涉嫌 \(AB\) 上，则所求距离为 \(QB\)
判断 \(Q\) 的位置建议用点积确定

double DistanceToSegment(Point P,Point A,Point B){
    if(A==B) return Length(P-A);
    Vector v1=B-A,v2=P-A,v3=P-B;
    if(dcmp(Dot(v1,v2))<0) return Length(v2);
    else if(dcmp(Dot(v1,v3)>0)) return Length(v3);
    else return fabs(Cross(v1,v2))/Length(v1);
}

点在直线上的投影

我们把直线 \(AB\) 写成参数式 \(A+tv\) （\(v\) 为向量 \(AB\)）且设 \(Q\) 的参数为 \(t_0\) 那么 \(Q=A+t_0v\) 根据 \(PQ\) 垂直于 \(AB\)，两个向量的点积应该为 \(0\)，可以得出 \(v \cdot (P-(A+t_0v))=0\) 根据分配律有 \(v \cdot (P-A)-t_0 \cdot (v \cdot v)=0\) 就能解出 \(t_0\) 了

//点在直线上的投影
Point GetLineProjection(Point P,Point A,Point B){
    Vector v=B-A;
    return A+v*(Dot(v,P-A)/Dot(v,v));
}

线段相交判定

我们定义两条线段相交的冲要条件是，每条线段的两个端点都在另一条线段的两侧(叉积的符号不同)，不包括在端点处相交

bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2){
    double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1),c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
    return dcmp(c1)*dcmp(c2)<0 && dcmp(c3)*dcmp(c4)<0;
}

如果允许在端点处相交

  • 如果 \(c_1,c_2\) 都是 \(0\) , 表示两线段共线
  • 如果 \(c_1,c_2\) 不都是 \(0\) ,则只有一种相交方法，即某个端点在另外一条线段上，为了判断上述情况是否发生，还需要如下一段代码判断一个点是否在一条线段上(不包含端点)
bool OnSegment(Point p,Point a1,Point a2){
    return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p));
}

多边形

把多边形从第一个顶点出发把凸多边形分成 \(n-2\) 个三角形，然后把面积加起来

其实这个方法对非凸多边形也适用，因为三角形的面积是有向的，在外面的部分可以抵消掉

//判断一个点是否在一条线段上
bool OnSegment(Point p,Point a1,Point a2){
    return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p));
}