会议:IJCAI,时间:2023,学校:1 中国科学院计算机网络信息中心,北京 2中国科学院大学,北京 3 澳门大学智慧城市物联网国家重点实验室,澳门 4 香港科技大学(广州),广州 5 佛罗里达大学计算机科学系,奥兰多
摘要:
提出一种新的具有TKG关联特征的体系结构建模方法,即自适应路径-记忆网络(DaeMon)。该模型对查询主题和每个候选对象之间跨越历史时间的时间路径信息进行自适应建模,而不依赖实体表示。具体来说,DaeMon使用路径内存来记录从路径聚合单元派生的时间路径信息,并考虑相邻时间戳之间的内存传递策略。
介绍:
本文的重点侧重于TKG推理中的外推部分,具体设计了一个模型来预测未来时间戳的链接。之前的方法中,历史上出现的实体是建模结构和时间特征的关键组成部分:(a)对于结构特征,实体及其各自相邻实体的识别是必不可少的,因为大多数当前模型利用从历史事实中提取的结构信息作为TKG推理的基础。随之出现的问题是对于没有历史背景的情况很难预测。
在本文中,我们将集中研究时间路径作为一种以新颖和独立于实体的方式利用历史事件信息的手段。通过考虑查询实体和任何候选实体之间存在的整个时间路径,我们能够推断它们之间将来可能发生的潜在关系。由时间路径连接的中间实体的身份以及它们是新实体还是预先存在的实体,对最终预测没有影响,从而使这种建模方法完全独立于实体。下图说明了时间路径是独立于实体的
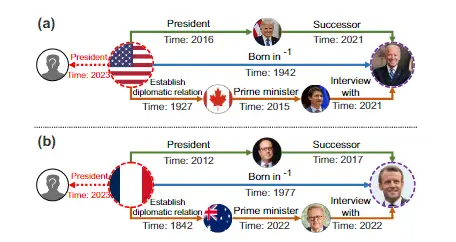
本文工作:尝试对查询主题实体和候选对象实体之间的所有时间路径进行建模,并提出了一种具有时间轴上关系特征的新型体系结构建模。该模型由三部分组成(1)路径记忆(2)路径聚合单元(3)内存传递策略
相关工作:
一.静态知识图谱推理:GNN逐渐成为主流,效果很好,但无法预测未来时间
二.时态知识图谱推理:仍然需要灵活高效、能够处理长期依赖关系和可扩展需求的TKG推理模型
问题的数学化描述:
与之前类似,本文对于知识图谱的定义依然是四元组(s,r,o,t)。我们要解决的问题是,根据给出的 \({\left\{ \left( s,r,o,t_i \right) |t_i<t_q \right\}}\)来预测 \({(s,r,?,t_q)}\)而tq期间的事实未知。具体来说,我们将E中的所有实体视为候选实体,并通过分数函数对它们进行排序,以预测给定查询的缺失对象。此外,对于时序知识图谱中的每个事实,我们相应地将逆四元组 \({(o,r^{-1},s,t)}\)插入到Gt之中。
模型方法:
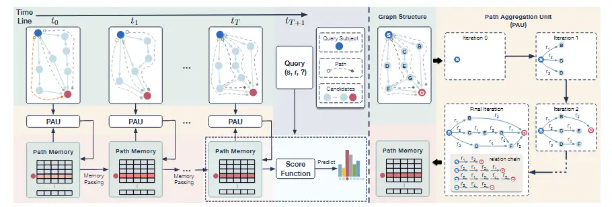
上图是模型的框架概述。我们以查询主题(深蓝色节点)和所选对象候选(深红色节点)之间的建模时间路径为例,为了清楚起见,仅显示路径内存更新过程只关注所选对象候选。
一.模型概述:
DaeMon的主要思想是在考虑查询关系r的同时,利用顺序子图自适应地对查询主题s和每个对象候选 \({o_i∈E}\)之间的查询感知路径信息进行建模。
1.通过不断更新收集到的路径信息来捕获跨时间的连接信息
2.为了保存,构建了路径内存,以暂时保留当前收集信息的状态
3.根据内存状态,使用路径聚合单元对s到 \({o_i∈E}\)之间的综合路径信息进行处理和建模
此外,本文提出了内存传递策略来引导相邻时间之间的内存状态传递。基于存储在内存中的最终学习到的查询感知路径信息,可以使用匹配函数对未来时间戳进行推理。
高级思想:捕获子图序列之间的关系链模式。
路径记忆:
核心操作:构建查询感知内存单元,将获取到的过去路径信息缓存到后续处理中使用,以便在后续查询中不断细化。
数学公式: \({\mathbf{M}_{\left( s,r \right) \rightarrow \mathcal{E}}^{t}\in \mathbb{R} ^{|\mathcal{E} |\times d}}\)内存在t时刻的状态,其中|E|为候选集合的基数,d为路径嵌入的维数。
具体操作:给定一个查询(s, r, ?),我们以对象候选oi为例。我们所考虑的和oi之间的路径信息是所有以s开始并以oi结束的路径的聚合形式。由于我们的目标是捕获跨越历史时间轴的路径信息,我们最终可以获得存储在最后一个历史时间戳T的内存中的完整路径信息表示 \({\mathbf{m}_{\left( s,r \right) \rightarrow o_i}^{T}\in \mathbf{M}_{\left( s,r \right) \rightarrow \mathcal{E}}^{T}}\)
形式描述: \({\mathbf{m}_{\left( s,r \right) \rightarrow o_i}^{t}=MPS\left( \mathbf{m}_{\left( s,r \right) \rightarrow o_i}^{t-1} \right) \oplus PAU\left( \mathcal{P} _{s\rightarrow o_i}^{t} \right)}\)
\({PAU\left( \mathcal{P} _{s\rightarrow o_i}^{t} \right) =\mathbf{p}_{0}^{t}\oplus \mathbf{p}_{1}^{t}\oplus …\oplus \mathbf{p}_{|\mathcal{P} _{s\rightarrow o_i}^{t}|}^{t}|_{p_{k}^{t}\in \mathcal{P} _{s\rightarrow o_i}^{t}}}\)
其中MPS(·)表示内存传递策略,旨在继承前一个时间戳的内存状态;PAU(·)是路径聚合单元,聚合查询主题 s 和对象候选 oi 之间的路径信息。⊕ 表示路径聚合算子。\({P_{s\rightarrow o_i}^t}\)表示时间戳 t 从 s 到 oi 的路径集。当\({{p_{k}^{t}\in \mathcal{P} _{s\rightarrow o_i}^{t}}}\)确定时,证明其中包含:
\({\mathbf{p}_{k}^{t}=\mathbf{w}_r\left( e_0 \right) \otimes \mathbf{w}_r\left( e_1 \right) \otimes \cdots \otimes \mathbf{w}_r\left( e_{|p_{k}^{t}|} \right)}\)
\({w_r(e_*)}\)是边 \({e_*}\)的r感知表示,⊗表示合并路径\({p^t_k}\)中边缘信息的算子
路径聚合单元:
PAU是处理特定主题 s 和所有候选 oi ∈ E 之间的路径信息的表示,同时考虑特定的查询关系类型 r。
我们设计了一种时间路径聚合方法来不断学习时间线上的历史子图结构。如之前所说,由于路径特征在不考虑时间的情况下一直是静态的,所以PAU会随着时间的发展自适应地细化内存,和之前历史中的路径进行聚合。
数学表达:
对于一个给定的查询(s,r,?),该网络基于时间戳 t 处子图的先前记忆状态和拓扑, \({P_{s \rightarrow \mathcal{E}}^t}\)对于所有的 \({o_i\in\mathcal{E}}\)的路径信息将由 w 层 r 感知路径聚合神经网络学习。在完成 w 层聚合迭代后,内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^t}\) 将更新为聚合路径信息。
我们可以使用 \({\mathbf{H}_{(s,r)\rightarrow \mathcal{E}}^{t,l}\in\mathbb{R}^{|\mathcal{E}|\times d}}\)表示第l层迭代路径信息状态, \({\mathbf{h}_{(s,r)\rightarrow o_i}^{t,l}\in\mathbf{H}_{(s,r)\rightarrow \mathcal{E}}^{t,l}}\)表示候选oi在第l层迭代时的状态,其中l∈[0,w],d是路径嵌入的维数。当l=0时, \({\mathbf{H}_{(s,r)\rightarrow \mathcal{E}}^{t,0}}\)表示迭代在时间戳处的初始状态。我们将 \({\mathbf{h}_{(s,r)\rightarrow o_i}^{t,l},\mathbf{H}_{(s,r)\rightarrow \mathcal{E}}^{t,l}}\)缩写成 \({\mathbf{h}_{o_i}^{t,l},\mathbf{H}_{\mathcal{E}}^{t,l}}\)。那么,我们可以将以时间戳t的PAU迭代过程为例描述如下:
\({\mathbf{h}_{o_i}^{t,l}=AGG(\left\{ MSG\left( \mathbf{h}_{z}^{t,l-1},\mathbf{w}_r\left( z,p,o_i \right) \right) |\left( z,p,o_i \right) \in G_t \right\})}\)
式中,AGG(·)和MSG(·)为聚合函数和消息生成函数,分别对应式2和式3中的算子;Wr表示边型p的r感知表示;(z,p,oi)∈Gt是子图Gt中的一条边,其中关系p发生在实体z与候选实体oi之间。
此外,我们提前初始化了所有具有可学习参数 \({\mathbf{R}\in\mathbb{R}^{|\mathcal{R}|\times d}}\)的关系类型表示,并将嵌入r∈R的查询关系项目化为用于消息生成的R感知关系表示。wr的数学表达如下:
\({\mathbf{w}_r(z,p,o_i)=\mathbf{W}_p\mathbf{r}+\mathbf{b}_p}\)
对于MSG函数,我们使用乘法的矢量化方法,其中算子⊗被定义为h和w之间的元素乘法。在我们的路径信息建模中,乘法操作可以解释为将 $ \mathbf{h}_z^{t,l-1}
$缩放为 \({\mathbf{w}_r(z,p,o_i)}\):
\({MSG\left( \mathbf{h}_{z}^{t,l-1},\mathbf{w}_r\left( z,p,o_i \right) \right) =\mathbf{h}_{z}^{t,l-1}\otimes \mathbf{w}_r\left( z,p,o_i \right)}\)
对于AGG函数,我们采用了[Corso et al., 2020]中提出的主邻域聚合(PNA)。经过w层聚合迭代后,路径内存 \({\mathbf{m}_{(s,r)\rightarrow o_i}^{t}\in\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t}}\)最终更新为 \({\mathbf{h}_{o_i}^{t,w}\in\mathbf{H}_{\mathcal{E}}^{t,w}}\)。 \({\mathbf{H}_{\mathcal{E}}^{t,0}}\)通过内存传递策略利用最后相邻的内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\)进行初始化。若不存在前一层内存状态,只有当oi等于查询主题s即 \({\mathbf{h}_s^{0,0}\leftarrow r}\)时,我们才初始化第一层之前实体i上的查询关系嵌入r,否则为零嵌入。对于t > 0的情况,采用内存传递策略设置PAU迭代的初始状态 \({\mathbf{H}^{t,0}_{\mathcal{E}}}\)。
内存传递策略:
为了捕获跨越时间的路径信息,我们继续改进先前维护的路径信息。我们设计了一种内存传递策略,目的是应对相邻拓扑结构的变化。 \({\mathbf{H}^{0,0}_{\mathcal{E}}}\)在时间(t = 0)开始时通过查询关系表示进行初始化,对于t > 0,初始状态 \({\mathbf{H}_{\mathcal{E}}^{t,0}}\)应该继承之前的内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\),即最后一层状态 \({\mathbf{H}_{\mathcal{E}}^{t-1,w}}\),该层在时间戳t−1之前已经收集了路径信息。
根据上述情况,我们选择设计一种时间感知的门控内存传递策略;初始状态 \({\mathbf{H}^{t,0}_{\mathcal{E}}}\)由两部分决定,即时间戳t−1时最开始的初始状态 \({\mathbf{H}^{0,0}_{\mathcal{E}}}\)和最后学习到的内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\)。从数学形式上: \({\mathbf{H}_{\mathcal{E}}^{t,0}=\mathbf{U}_t\odot \mathbf{H}_{\mathcal{E}}^{0,0}+\left( 1-\mathbf{U}_t \right) \odot \mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\),式中⊙表示哈达玛乘积运算。时敏门矩阵 \({\mathbf{U}_t\in\mathbb{R}^{|\mathcal{E}|\times d}}\)应用非线性变换为: \({\mathbf{U}_t=\sigma \left( \mathbf{W}_{GATE}\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}+\mathbf{b}_{GATE} \right) }\)其中σ(·)为sigmoid函数, \({\mathbf{W}_{GATE}\in \mathbb{R}^{d\times d}}\)为时间感知门权矩阵参数。
学习与推理:
DaeMon具有迁移到使用预训练模型进行TKG预测的其他数据集的可转移性。接下来,我们将要介绍我们是如何对TKG进行未来推理,即我们的得分函数。给定查询主题s和查询关系r在时间戳T + 1,我们使用 \({\mathbf{m}_{\left( s,r \right) \rightarrow o_i}^{T}\in \mathbf{M}_{\left( s,r \right) \rightarrow \mathcal{E}}^{T}}\)预测未来对象候选对象oi∈E的条件似然为: \({p\left( o_i|s,r \right) =\sigma \left( \mathcal{F} \left( \mathbf{m}_{\left( s,r \right) \rightarrow o_i}^{T} \right) \right) }\),其中F(·)为前馈神经网络,σ(·)为s型函数。由于我们提前在数据集中加入了逆四元组 \({(o,r^{−1},s, t)}\),在不损失通用性的前提下,我们也可以在给定查询关系r和查询对象o的情况下,用相同的模型预测主题si∈E: \({p\left( s_i|o,r^{-1} \right) =\sigma \left( \mathcal{F} \left( \mathbf{m}_{\left( o,r^{-1} \right) \rightarrow s_i}^{T} \right) \right) }\)。最后,本文分析了参数学习:对给定查询的推理可以看作是一个二元分类问题。我们将正负三元组的负对数似然最小化为 \({\mathcal{L} _{TKG}=-\log p\left( s,r,o \right) -\sum_{j=1}^n{\frac{1}{n}\log \left( 1-p\left( \overline{s_j},r,\overline{o_j} \right) \right)}}\),其中 n 是每个正样本负样本数的超参数; (s, r, o) 和 (sj , r, oj ) 分别是正样本和第 j 个负样本。根据部分完整性假设,在每个推理时间戳生成负样本。也就是说,我们在正三元组中破坏其中一个实体,以从推理的未来三元组集中创建一个负样本。为了鼓励在开始时初始化的可学习参数 R 中的正交性,在目标函数中添加了正则化项 \({\mathcal{L} _{REG}=\left\| \mathbf{R}^T\mathbf{R}-\alpha \mathbf{I} \right\| }\),其中 I 是单位矩阵,α 是超参数,∥ · ∥ 表示 L2-norm。因此,DaeMon 的最终损失可以表示为: \({\mathcal{L}=\mathcal{L}_{TKG}+\mathcal{L}_{REG}}\)
实验:
数据集:ICEWS18,GDELT,WIKI,YAGO

通过时间戳将数据集分割为训练/有效/测试(训练的时间戳)<(有效的时间戳)<(测试的时间戳)
评估指标:为了评估所提出的模型对 TKG 推理的性能,我们还选择了广泛使用的链接预测任务,用于未来时间戳。报告平均倒数排名 (MRR) 和 Hits@{1, 3, 10} 作为评估指标来评估所提出模型的性能。
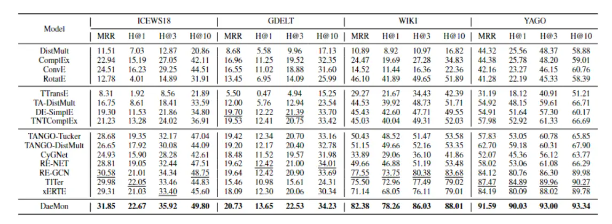
基线方法:
1.KG推理方法:DistMult[Yang et al., 2014]、ComplEx [Trouillon et al., 2016]、ConvE [Dettmers et al., 2017]和RotatE [Sun et al., 2019]
2.插值TKG推理模型:TTransE [Leblay和Chekol, 2018]、TADistMult [Garcia-Duran等人,2018]、DE-SimplE [Goel等人,2020]和TNTComplEx [Lacroix等人,2020]
3.外推TKG推理模型: TANGOTucker [Han et al., 2021]、TANGO-DistMult [Han et al., 2021]、CyGNet [Zhu et al., 2021a]、RE-NET [Jin et al., 2020]、RE-GCN [Li et al., 2021]、TITER [Sun et al., 2021] 和 xERTE [Han et al., 2020]
设置参数:
对于 Memory 和 PAU,嵌入维度 d 设置为 64;路径聚合层数 w 设置为 2;聚合的激活函数为 relu。层归一化和快捷方式在聚合层上进行。对于参数学习,负样本数设置为64;正则化项中的超参数α设为1。采用Adam [Kingma and Ba, 2014]进行学习率为5e−4的参数学习,最大训练周期设置为30。
历史长度分析:
DaeMon强烈依赖于图的拓扑连通性;对于图 3(a,b) 所示的 ICEWS18 和 GDELT,它们的区间比前者短得多。因此,它们需要更长的历史来提高准确性。

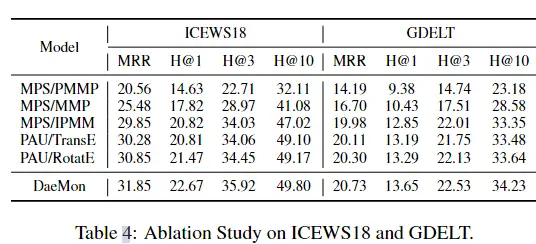
消融研究:
1)我们对前一个内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\) 进行平均池化,即在当前处理时间戳 t 之前已经对路径信息进行编码的最后一层状态,并直接传递给当前初始状态 \({\mathbf{H}^{t,0}_{\mathcal{E}}}\) ,表示为 MPS/PMMP。MPS/PMMP对最终结果的影响更显著,因为它破坏了之前收集的路径信息。
2)去掉传递步骤,将每个初始状态 \({\mathbf{H}^{t,0}_{\mathcal{E}}}\)初始化为 \({\mathbf{H}^{0,0}_{\mathcal{E}}}\)相同,最后每次计算每个更新层状态 \({\mathbf{H}^{t,w}_{\mathcal{E}}}\)的平均值,记为MPS/MMP。它还具有不良的结果,因为它忽略了序列模式信息和过程路径,而不考虑连续性
3)我们将提出的门控传递策略替换为Mean算子,计算最开始的初始状态 \({\mathbf{H}^{0,0}_{\mathcal{E}}}\)和先前学习的内存状态 \({\mathbf{M}_{(s,r)\rightarrow \mathcal{E}}^{t-1}}\)的平均值作为时间戳t处的初始层状态 \({\mathbf{H}^{t,0}_{\mathcal{E}}}\),记为MPS/IPMM。直观地说,它属于所提出策略的一个特例,很难自动适应时间序列和路径特征的多样性
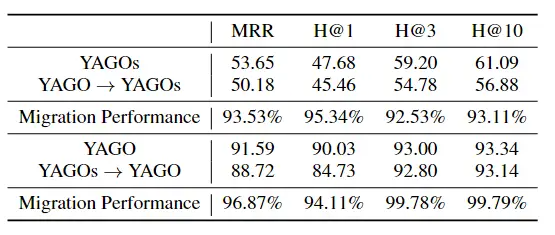
迁移效果: