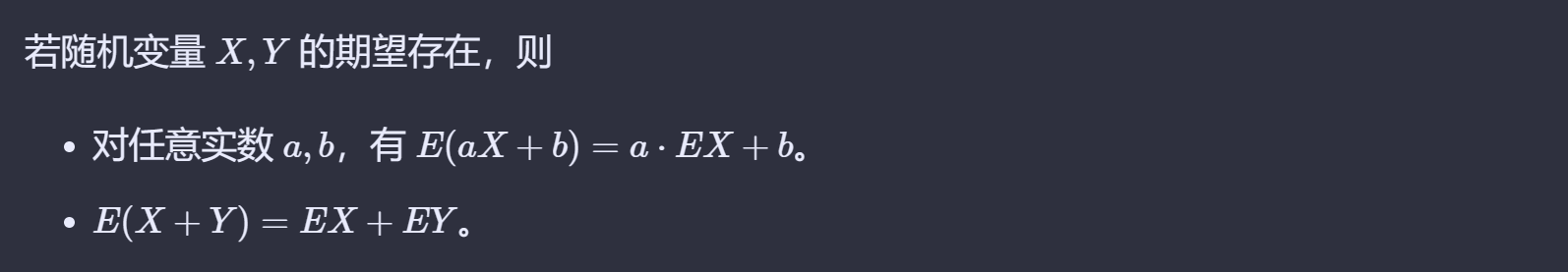期望的线性性

例1·CodeForces - 453A

题解

我们定义随机变量$X=x$ 代表独立投掷$n$次的最大点数为$x$

对于离散变量的概率，具有类似前缀和的性质：

\[P(X=k) =P(X \leq k) - P(X \leq k-1)\\ =(\frac{k}{m})^n - (\frac{k-1}{m})^n \]

\[\]

\[ * 所以我们直接$O(m)$枚举点数即可 \]

const int N = 2e5 + 10, M = 4e5 + 10;

int n, m;

void solve()
{
    cin >> m >> n;
    double ans = 0.0;
    for (int i = 1; i <= m; ++i)
    {
        ans += (pow(1.0 * i / m, n) - pow(1.0 * (i - 1) / m, n)) * i;
    }
    cout << fixed << setprecision(12) << ans << endl;
}

例2·CF1612E Messages

题解

我们定义随机变量$X = x$ 代表读到自己对应消息的学生的数量为$x$，$Y_i = 0 / 1$ 代表第$i$个人有没有读到自己对应的消息

利用随机变量的可加性得：$X = Y_1 + Y_2+...+Y_n$，对于$Y_i$的取值只有$0$和$1$两种情况，$1$代表第$i$个人读到了自己对应的消息，$0$代表第$i$个人没有读到了自己对应的消息

根据期望的线性性可知，读到自己对应消息的学生数量的期望$E[X] = E[Y_1]+E[Y_2]+...+E[Y_n]$

我们考虑每个人的$E[Y_i]$，因为只有两种情况，所以

\[E[Y_i] = 0 \times P(Y_i = 0)+1 \times P(Y_i = 1)\\ E[Y_i] = P(Y_i = 1) \]

所以每个人的$E[Y_i]$就等于每个人读到自己对应消息$m_i$的概率

所以我们把题目转化为求每个人读到自己对应消息$m_i$的概率之和的最大值

接下来我们考虑如何计算每个人读到自己对应消息$m_i$的概率

假设我们已经确定了$t$则消息，分别为$c_1,c_2...c_t$

如果这$t$则消息中不包含$m_i$，那么读到消息的概率一定为$0$

如果这$t$则消息中包含$m_i$，且$t \leq k_i$，那么读到消息的概率一定为$1$

如果这$t$则消息中包含$m_i$，且$t > k_i$，那么读到消息的概率为$\frac{C_{t-1}^{k_i-1}}{C_{t}^{k_i}}=\frac{k_i}{t}$

假设我们确定了$t$，那么每个人的$E[Y_i]$期望都可以通过上面的式子$O(1)$得到，所以我们$O(n)$枚举每个人求出选每一个$m_i$能够产生的贡献，那么贡献之和就是$E[X]$，所以现在的关键是怎样枚举$t$

观察到题目中$k_i<=20$的情况，对于$t <= 20$的时候，我们不妨直接暴力枚举$t$，贪心取前$t$个最大的消息对答案产生的贡献

对于$t \geq 21$的时候，我们没有必要枚举，因为只会出现第$3$种情况，所以随着$t$的变大答案只会越来越小，最优值一定会出现在$t \leq 20$的情况中

时间复杂度$O(20 \times mlog\ m)$

const int N = 2e5 + 10, M = 4e5 + 10;

int n;
int m[N], k[N];
vector<int> ans;

void solve()
{
    cin >> n;
    for (int i = 1; i <= n; ++i)
        cin >> m[i] >> k[i];
    double mx = 0;
    for (int t = 1; t <= 20; ++t)
    {
        vector<pii> vec(N); // 记录选择每个消息能够产生的贡献
        double sum = 0;
        for (int i = 1; i <= n; ++i)
        {
            vec[m[i]].first += min(t, k[i]);
            vec[m[i]].second = m[i];
        }
        sort(all(vec), greater<pii>()); // 将贡献排序
        vector<int> tmp;
        for (int i = 0; i < t; ++i) // 贪心选择前t个消息
        {
            sum += vec[i].first;
            if (vec[i].second)
                tmp.push_back(vec[i].second);
        }
        sum /= t; // 不要忘记除以t
        if (sum > mx)
        {
            mx = sum;
            ans = tmp;
        }
    }
    cout << ans.size() << endl;
    for (auto it : ans)
        cout << it << " ";
    cout << endl;
}

期望DP

上面的题目基本都是直接基于期望的性质或者定义来进行计算，但很多题目是无法直接计算的

期望DP一般通过记忆化搜索的方式进行DP

DP模型

给出一个有向无环图($DAG$)，每条有向边有一个权值$w_u$，一个人从节点$x$出发，假设当前处于节点$u$，则：

如果节点$u$不存在连向其他任何点的边，则过程停止

如果节点$u$存在连向其他点的边，人从$u$随机的走向它的邻点$v$的概率为$P_{u,v}$，其中$\sum_{v邻接于u}P_{u,v} = 1$，$u$和$v$是有边相邻的点，且两者之间路程（边权）为$w_{u,v}$

求人从$x$出发直到停止走过的总路程的期望

我们定义随机变量$D_u=d$ 代表从$x$出发到$u$停止时走过的总路程为$d$，则：

$E[D_u] = \sum_d d \times P(D_u = d)$

我们再定义随机变量$Next_u = v$ 代表$v$是与$u$相连的点，则：

\[D_u = D_{Next_u} + W_{Next_u,u} \]
\[\begin{flalign} E[D_u] =&\sum_d d \times P(D_u = d)\\ =&\sum_d d \times \sum_v P(u,v)\times P(D_v = d - w_{u,v})\\ =&\sum_v P(u,v)\times \sum_d d \times P(D_v = d - w_{u,v})\\ =&\sum_v P(u,v)\times \sum_{d'} (d' + w_{u,v}) \times P(D_v = d')\ \ (令d'=d-w_{u,v})\\ =&\sum_v P(u,v)\times \{\sum_{d'} d' \times P(D_v = d') + \sum_{d'}w_{u,v} \times P(D_v = d') \}\\ =&\sum_v P(u,v) \times (E[D_v] + w_{u,v})&\\ \end{flalign} \]

\[\]

\[ * 实际上对于**有向有环图**来说，该公式也是**有效**的，只不过无法进行期望DP罢了 \]

例1·AtCoder - abc184_d

题解

由于按照期望的性质和定义比较麻烦得到答案，我们考虑期望DP

$f[i][j][k]$代表金币状态为$(i,j,k)$时操作次数的期望

我们考虑DP的状态转移：

\[\]

\[\]

const int N = 1e2 + 10, M = 4e5 + 10;

int A, B, C;
double f[N][N][N];

double dfs(int a, int b, int c)
{
    if (a >= 100 || b >= 100 || c >= 100)
        return 0;
    if (f[a][b][c] != 0)
        return f[a][b][c];
    double ans = 0;
    double p1 = (1.0 * a) / (a + b + c), p2 = (1.0 * b) / (a + b + c), p3 = (1.0 * c) / (a + b + c);
    ans = p1 * (dfs(a + 1, b, c) + 1) + p2 * (dfs(a, b + 1, c) + 1) + p3 * (dfs(a, b, c + 1) + 1);
    return f[a][b][c] = ans;
}

void solve()
{
    cin >> A >> B >> C;
    memset(f, 0, sizeof f);
    f[A][B][C] = dfs(A, B, C);
    cout << fixed << setprecision(8) << f[A][B][C] << endl;
}

例2·Timaeus

题解

我们考虑期望DP

我们定义$f[x]$为有$x$个材料最多能够合成材料数量的期望

我们考虑状态的转移，两个人分为两种情况：

如果我们选择第一个人，有$p$的概率获得双倍合成材料，有$1-p$的概率不获得双倍合成材料

\[f[x] = \frac{p}{100} \times(f[x - B] + 2) + (1 - \frac{p}{100}) \times (f[x - B] + 1) \]

如果我们选择第二个人，有$q$的概率返还一个材料，有$1-q$的概率不返还一个材料

\[f[x] = \frac{q}{100}\times(f[x - B + 1] + 1) + (1 - \frac{q}{100}) \times (f[x - B] + 1) \]

但是我们发现当$B = 1$的时候，会从$DAG$变成有自环的有向图，即使刚刚推导的公式可以使用，但是我们无法DP

但是如果我们将$B = 1$代入第二个状态转移的式子后，容易得到:

\[f[x] = dp[x - 1] + \frac{100}{100 - q}\ \ (B = 1) \]

所以当$B = 1$时按照上述式子转移即可

const int N = 1e6 + 10, M = 4e5 + 10;

// p / 100 * (f[x - B] + 2) + (1 - p / 100) * (f[x - B] + 1)
// q / 100 * (f[x - B + 1] + 1) + (1 - q / 100) * (f[x - B] + 1)

int a, b, p, q;
double f[N];

double dfs(int x, int b, int p, int q)
{
    if (x < b)
        return 0;
    if (f[x] != 0)
        return f[x];
    double ans = 1.0 * p / 100 * (dfs(x - b, b, p, q) + 2) + (1 - 1.0 * p / 100) * (dfs(x - b, b, p, q) + 1);
    if (b == 1)
    {
        ans = max(ans, dfs(x - 1, b, p, q) + (100.0 / (100 - q)));
    }
    else
    {
        ans = max(ans, 1.0 * q / 100 * (dfs(x - b + 1, b, p, q) + 1) + (1 - 1.0 * q / 100) * (dfs(x - b, b, p, q) + 1));
    }
    return f[x] = ans;
}

void solve()
{
    cin >> a >> b >> p >> q;
    cout << fixed << setprecision(10) << dfs(a, b, p, q) << endl;
}

例3·Fork in the Road

题解

我们考虑期望DP

我们定义$f[u]$代表从$u$到$N$号房间要走的通道数的期望

题目要求我们堵塞一条路，我们先考虑$O(m)$枚举所有边，然后将这条边删去后$O(m)$再做一遍期望DP，所以时间复杂度为$O(m^2)$，显然不可行

但是容易发现如果我们枚举每个节点，对其最大的$dp$贡献值的边删去后，再做一遍期望DP，时间复杂度为$O(m\times n)$

const int N = 6e2 + 10, M = 4e5 + 10;

int n, m;
vector<int> g[N];
int deg[N];
double f[N];
double dp[N];
bool vis[N][N];
bool st[N];

double dfs(int u)
{
    if (u == n)
        return 0;
    if (f[u])
        return f[u];
    double ans = 0;
    for (auto v : g[u])
    {
        ans += (1.0 / deg[u]) * (dfs(v) + 1);
    }
    return f[u] = ans;
}

double DFS(int u)
{
    if (u == n)
        return 0;
    if (dp[u])
        return dp[u];
    double ans = 0;
    for (auto v : g[u])
    {
        if (vis[u][v])
            continue;
        if (st[u])
            ans += (1.0 / (deg[u] - 1)) * (DFS(v) + 1);
        else
            ans += (1.0 / deg[u]) * (DFS(v) + 1);
    }
    return dp[u] = ans;
}

void solve()
{
    cin >> n >> m;
    for (int i = 1; i <= m; ++i)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        ++deg[u];
    }
    double ans = INF;
    ans = min(ans, dfs(1));
    for (int i = 1; i <= n; ++i)
    {
        int u = i;
        if (deg[u] == 1)
            continue;
        double mx = 0;
        int p = -1;
        for (auto v : g[u])
        {
            if (mx < (f[v] + 1) * (1.0 / deg[u]))
            {
                mx = (f[v] + 1) * (1.0 / deg[u]);
                p = v;
            }
        }
        memset(dp, 0, sizeof dp);
        vis[u][p] = true;
        st[u] = true;
        ans = min(ans, DFS(1));
        vis[u][p] = false;
        st[u] = false;
    }
    cout << fixed << setprecision(10) << ans << endl;
}