论文信息

论文标题：Cross-domain Activity Recognition via Substructural Optimal Transport
论文作者：Wang Lu, Yiqiang Chen, Jindong Wang, Xin Qin
论文来源：Neurocomputing
论文地址：download
论文代码：download

1 背景

　　使用从传感器收集到的原始信号，学习有关人类活动的高级知识。应用于步态分析、手势识别、睡眠阶段检测等领域

　　跨域活动识别（CDAR）：借助辅助数据集，使用领域自适应的方式为无标签的新活动数据集构建模型

　　贝叶斯信息准则（BIC）：

- 背景：参数估计问题采用似然函数作为目标函数，提高模型复杂度可提高模型精度，但会导致过拟合问题发生，希望在模型复杂度与模型对数据集描述能力之间寻求最佳平衡；
- 公式：$\mathrm{BIC}=k \ln (n)-2 \ln (\widehat{L})$，其中后项为精度惩罚，$L$ 表示似然函数的值；前项为复杂度惩罚，$k$ 表示自由参数数量，$n$ 表示样本数量；
- 解释：增加参数数量会增大似然函数，但是参数过多时，似然函数增速减缓，易产生过拟合现象，选取使BIC最小的自由参数数量即可达到较优状态

　　最优输运问题（OT）：

- 概率向量：元素值在 $[0,1]$ 间，和为 $1$ 的数组
- 离散测度：将概率向量对应给某个数的函数

　　　　　　　　$\alpha=\sum_{i=1}^{n} \mathbf{a}_{i} \delta_{x_{i}}$

- 最优输运问题：对于两个测度，找到最优的映射方式 $P$，使下式成立（$C$ 为代价矩阵）：

　　　　　　　　$\mathrm{L}_{\mathbf{C}}(\mathbf{a}, \mathbf{b}) \stackrel{\text { def. }}{=} \min _{\mathbf{P} \in \mathbf{U}(\mathbf{a}, \mathbf{b})}\langle\mathbf{C}, \mathbf{P}\rangle \stackrel{\text { def. }}{=} \sum_{i, j} \mathbf{C}_{i, j} \mathbf{P}_{i, j}$

2 传统方法简介

　　分类

- 粗糙匹配：域级匹配/类级匹配/域级和类级匹配，通过学习域不变表示/类不变表示来匹配分布；
- 样本级匹配：实现两个域的成对样本对齐；

　　局部性：两个传感器信号之间的细粒度相似度

　　缺陷

- 粗糙匹配：忽略活动数据的局部信息，可能导致不适应；
- 样本级匹配：易受噪声点或异常值的影响，导致过度适应，学习局部信息时出现过拟合；匹配太多的点，耗时；

　　实验分析

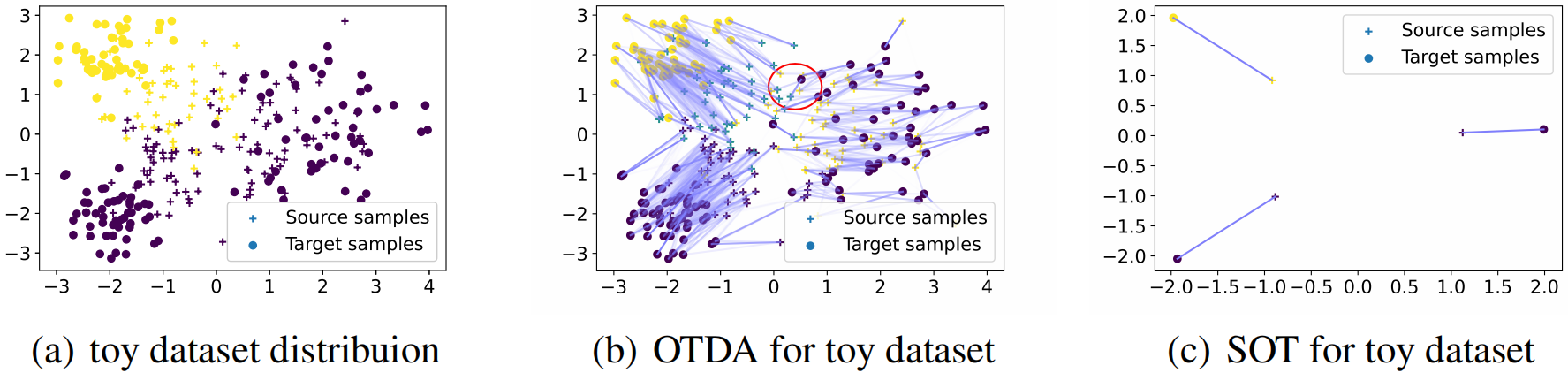
- 源域/目标域分别由高斯混合分别采样得到，对应于两个类和三个不同的簇；
- 由于其中一个类对应两个簇，使用粗糙匹配将忽略这种局部信息；
- 数据携带噪音或扰动，直接对数据样本进行匹配可能出现不匹配的情况；

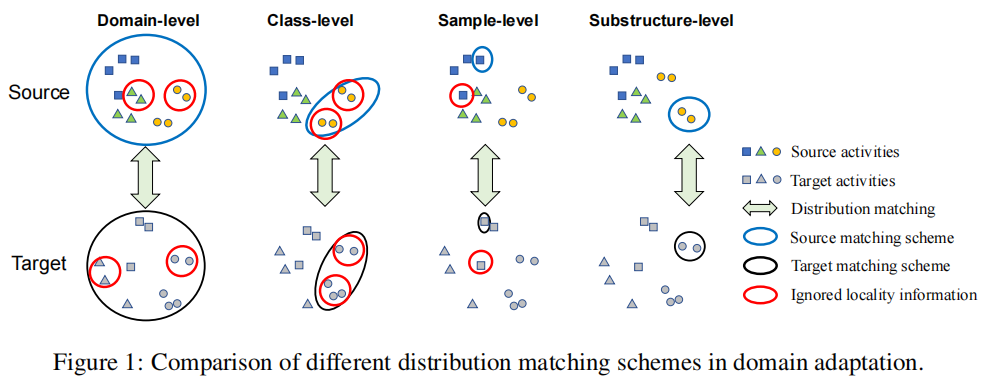
- 域级匹配完全忽略了域内数据结构；
- 类级匹配需要稍微精细的对齐；
- 样本级方法容易受到异常值影响，导致过拟合，且耗时；

3 子结构域自适应（SSDA）

　　子结构：描述数据的细粒度潜在分布，可理解为类内部簇，对应于局部信息；

　　优势

- 相较于粗略匹配，利用更细粒度的局部性信息（子结构），克服不适应问题；
- 相较于样本级匹配，避免噪声与异常值的过分影响，防止过度适应问题；
- 通用框架，可使用不同算法完成定制；

　　实现

　　　　基于最优传输，提出子结构最优传输（SOT）方法

　　　　步骤：

- - 通过聚类方法获得内部子结构；
  - 通过部分最优传输方法给出源域的活动子结构权值；
  - 学习匹配两个子结构上的概率分布函数的运输计划；

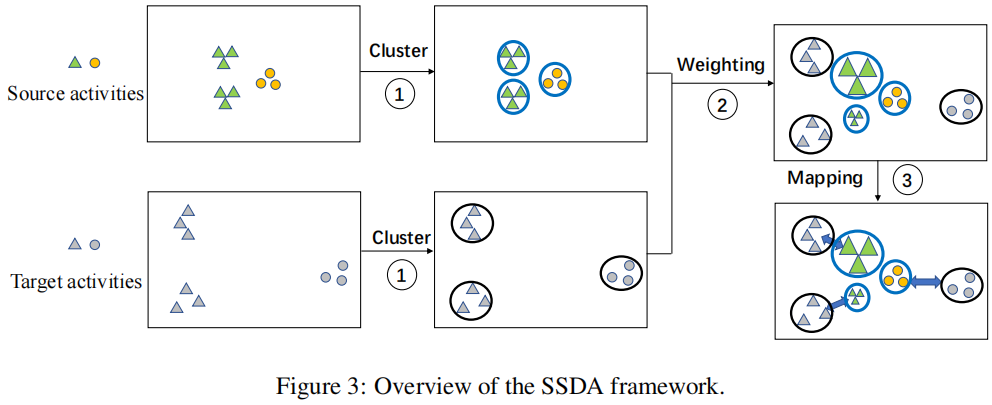
　　理论分析

　　　　域级匹配对象 $p(x)$，类级匹配对象 $p(x|y)$，进一步将域划分为更精细的子结构：

　　　　$\begin{aligned}p(\mathbf{x}) & =\sum_\limits{y} p(\mathbf{x} \mid y) p(y) \\& =\sum_\limits{y}\left(\sum_\limits{o} p(\mathbf{x}, o \mid y)\right) p(y) \\& =\sum_\limits{y} \sum_\limits{o} p(\mathbf{x} \mid y, o) p(y, o) \text { (For source domain) } \\& =\sum_\limits{o} \sum_\limits{y} p(\mathbf{x} \mid y, o) p(y \mid o) p(o) \\& =\sum_\limits{o} p(\mathbf{x} \mid o) p(o) . \text { (For target domain) }\end{aligned}$

　　重点观察

　　由于类和子结构之间的关系：

　　　　$p(y \mid o)=\left\{\begin{array}{ll}1 & o \text { is part of } y \\0 & o . w\end{array}\right.$

　　统一源域和目标域的匹配对象：

　　　　$p(\mathbf{x} \mid o)$

　　子结构最优运输（SOT）

　　步骤一：子结构生成和表示

　　$X$ 表示所有特征数据，$X_{k} \sim N\left(\mu_{k}, \sigma_{k}\right)$ 表示第 $k$ 个聚类的数据，服从高斯混合分布；可使用特征数据 $X$ 借助期望最大值（EM）算法获得高斯混合模型的参数。

　　针对源域为保持标签一致性，将其视为 $C$ 个高斯混合模型的混合分布，每个模型对应一个类，针对每个模型分别完成聚类；针对目标域由于缺少标签，直接对整个目标域完成聚类。

　　聚类数量由贝叶斯信息准则（$BIC$）决定，选取使 $BIC$ 最小的自由参数 $k$ 的数量来决定聚类的数量。

　　聚类算法可自由定制；

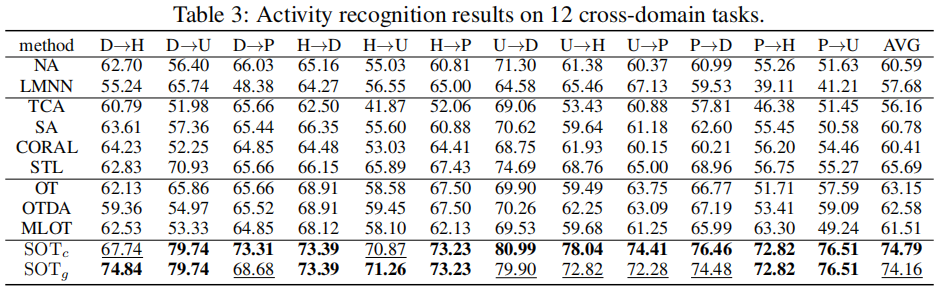
　　子结构表示：中心表示的 $S O T_{c}$ 表示法（只利用聚类中心，计算简单，效率高）与分布表示的 $S O T_{g}$ 表示法（利用更多聚类中心，计算时需近似）

　　$\operatorname{SOT}_{c}$ 表示法

　　目标域分布（源域类似）:

　　　　$\mu_{c, t}=\sum_{i=1}^{k_{t}} w_{t, i} \delta_{\mathbf{z}_{t, i}}$

　　其中 $z$ 表示聚类中心， $\delta_{z}$ 表示聚类中心处的 Dirac 函数, $\omega$ 表示与聚类中心相关的概率质量，和为 $1$。

　　使用欧式距离的平方作为两个域间聚类中心的距离度量: $\quad c\left(\mathbf{z}_{s, i}, \mathbf{z}_{t, j}\right)=\left\|\mathbf{z}_{s, i}-\mathbf{z}_{t, j}\right\|_{2}^{2}$ .

　　$\boldsymbol{SOT}_{g}$ 表示法

　　目标域分布（源域类似）：

　　　　$\mu_{g, t}=\sum_{i=1}^{k_{t}} w_{t, i} \mathcal{N}\left(\mathbf{z}_{t, i}, \boldsymbol{\sigma}_{t, i}\right)$

　　使用高斯分布代替聚类中心位置的 Dirac 函数使用 Wasserstein 距离的平方作为两个域间聚类中心的距离度量:

　　　　$c\left(\mathcal{N}\left(\mathbf{z}_{s, i}, \boldsymbol{\sigma}_{s, i}\right), \mathcal{N}\left(\mathbf{z}_{t, j}, \boldsymbol{\sigma}_{t, j}\right)\right)=W_{2}^{2}\left(\mathcal{N}\left(\mathbf{z}_{s, i}, \boldsymbol{\sigma}_{s, i}\right), \mathcal{N}\left(\mathbf{z}_{t, j}, \boldsymbol{\sigma}_{t, j}\right)\right)$

　　距离度量用于计算最优输运中的代价矩阵 $C$

　　将协方差矩阵强制为对角矩阵，经过转化的距离度量：

　　　　$\begin{aligned}c\left(\mathcal{N}\left(\mathbf{z}_{s, i}, \sigma_{s, i}\right), \mathcal{N}\left(\mathbf{z}_{t, j}, \sigma_{t, j}\right)\right) & =\left\|\mathbf{z}_{s, i}-\mathbf{z}_{t, j}\right\|^{2}+\left\|\sqrt{\mathbf{r}_{s, i}}-\sqrt{\mathbf{r}_{t, j}}\right\|_{2}^{2} \\& =\left\|\left(\mathbf{z}_{s, i}, \sqrt{\mathbf{r}_{s, i}}\right)-\left(\mathbf{z}_{t, j}, \sqrt{\mathbf{r}_{t, j}}\right)\right\|_{2}^{2}\end{aligned}$

　　其中 $r$ 表示簇的协方差矩阵的对角线，聚类中心 $z$ 和 $r$ 共同构成表示子结构的特征。

　　步骤二：计算子结构权值（概率质量）

　　对两种子结构表示法进行统一表示：

　　　　$P_{s}=\sum\limits_{s=1}^{k_{s}} w_{s, i} p_{s, i}$

　　对信息过少的目标域将 $\omega_{t, i}$ 固定为 $1 / k_{t}$ 自适应计算源域的子结构权值

　　由于 $ \omega$ 本身的特性 (和为 $1$）, 可看作概率分布向量，利用部分最优运输问题进行求解，求解最优运输方式对应的优化目标:

　　　　$\begin{array}{r}\boldsymbol{\pi}_{1}^{*}=\arg \min _{\pi}\langle\boldsymbol{\pi}, \mathbf{C}\rangle_{F}+\lambda_{1} H(\boldsymbol{\pi}) \\\text { s.t }\quad\quad\quad\quad\quad\quad \quad\boldsymbol{\pi}^{T} \mathbf{1}_{k_{s}}=\mathbf{w}_{t} \\\boldsymbol{\pi} \mathbf{1}_{k_{t}} \leq \mathbf{1}_{k_{s}} \\\mathbf{1}_{k_{t}}^{T} \boldsymbol{\pi}^{T} \mathbf{1}_{k_{s}}=1 .\end{array}$

　　其中 $\pi$ 为两个子结构概率分布函数的朱合合矩阵（co upling matrix)，$C$ 为代价矩阵，$\langle\cdot\rangle_{F}$ 为 Frobenius 点积，$\langle\pi, C\rangle_{F}$ 即为部分最优输运总代价，$H(\pi)$ 为便于计算加入的正则化项，定义式

　　　　$H(\boldsymbol{\pi})=\sum_{i j} \pi_{i j} \log \pi_{i j}$

　　可保证约束条件后两项必然成立，因此最终优化目标：$\boldsymbol{\pi}_{1}^{*}=\arg \min _{\boldsymbol{\pi}}\langle\boldsymbol{\pi}, \mathbf{C}\rangle_{F}+\lambda_{1} H(\boldsymbol{\pi})$

　　　　$\text { s.t } \quad \boldsymbol{\pi}^{T} \mathbf{1}_{k_{s}}=\mathbf{w}_{t} \text {. }$

　　由于约束条件为的可行解集为凸集，易得问题的封闭形式，可使用拉格朗日方法解决问题：

　　　　$L=\langle\boldsymbol{\pi}, \mathbf{C}\rangle_{F}+\lambda_{1} H(\boldsymbol{\pi})+\boldsymbol{\phi}^{T}\left(\boldsymbol{\pi}^{T} \mathbf{1}_{k_{s}}-\mathbf{w}_{t}\right)$

　　步骤三：基于最优输运（OT）的子结构映射

　　子结构最优运输 (SOT) 的总体优化目标:

　　　　$\begin{array}\boldsymbol{\pi}^{*}&=\arg \min _{\boldsymbol{\pi}}\langle\boldsymbol{\pi}, \mathbf{C}\rangle_{F}+\lambda H(\boldsymbol{\pi})+\eta \Omega(\boldsymbol{\pi}) \\\text { s.t } & \boldsymbol{\pi}^{T} \mathbf{1}_{k_{s}}=\mathbf{w}_{t} \\& \boldsymbol{\pi} \mathbf{1}_{k_{t}}=\mathbf{w}_{s} .\end{array}$

　　其中 $ \Omega(\pi)$ 为群稀疏正则化器，期望每个目标样本只从具有相同标签的源样本接收质量。

　　通过广义条件梯度 (GCG) 求解最优输运问题得到最优耦合矩阵 $\pi^{*}$ 后, 可通过重心咉射计算出变换后的 $\boldsymbol{p}_{s, i}$ 的值:

　　　　$\hat{\mathbf{p}}_{s, i}=\arg \min _{\mathbf{p}} \sum_{j} \pi^{*}(i, j) c\left(\mathbf{p}, \mathbf{p}_{t, j}\right)$

　　当代价函数为欧式距樆时, 可表示为

　　　　$\hat{\mathbf{P}}_{s}=\operatorname{diag}\left(\boldsymbol{\pi}^{*} \mathbf{1}_{k_{t}}\right)^{-1} \boldsymbol{\pi}^{*} \mathbf{P}_{t}$

　　其中 $P_{t}$ 为目标表示，$\widehat{P_{s}}$ 为源映射表示
　　使用计算出的 $ \widehat{P_{s}}$ 和标签 $ Y_{s}$ 可建立模型以预测 $ P_{t}$ 对应标签，将预测出的标签拭予目标域中属于对应聚类的数据即可最终完成目标域的标签预测任务，即实现跨域活动识别任务。