古典解:Schauder理论
Poisson方程和Newton位势
1:一些记号
回顾我们在调和方程中得到的一些结果.
基本解:
\[\Gamma(x-y)=\begin{cases}
\dfrac{1}{n(2-n)\omega_n}\dfrac{1}{|x-y|^{n-2}},&n\ge 3\\
\dfrac{1}{2\pi }\ln |x-y|,&n=2
\end{cases}
\]
对于区域\(\Omega\),以及\(f\in L(\Omega)\),我们称:
\begin{equation}
w(x):=\int_{\Omega}\Gamma(x-y)f(y)dy
\end{equation}
为函数\(f\)的Newton位势.
设\(x_0\)是区域\(D\)中一点,\(0 < \alpha < 1\),称\(f\)在\(x_0\)处具有指数为\(\alpha\)的Holder连续性,如果:
\[ [f]_{\alpha;x_0}:=\sup_{D}\frac{|f(x)-f(x_0)|}{|x-x_0|^{\alpha}}
\]
是有限的,称\(f_{\alpha;x_0}\)是\(f\)关于\(D\)在\(x_0\)处的\(\alpha\)解Holder系数.
如果
\[\begin{equation}
[f]_{\alpha,D}:=\sup_{x,y\in D,x\ne y}\frac{|f(x)-f(x_0)|}{|x-x_0|^{\alpha}}
\end{equation}
\]
是有限的,则称\(f\)在\(D\)中具有指数为\(\alpha\)的Holder连续性.(下称\(\alpha\)阶Holder连续性).
如果(eq:3)只是在\(D\)的任意一个紧子集上有限的,则称\(f\)在\(D\)中\(\alpha\)阶局部的Holder连续性.
下边回顾一下连续函数空间以及Holder连续函数空间的一些范数.
对\(C^k(\bar{\Omega})\)函数空间,我们可以定义其拟范数为:
\[[u]_{k;\Omega}:=|D^ku|_{0;\Omega}=\sup_{|\beta|=k}\sup_{\Omega}|D^\beta u|
\]
以及范数:
\[||u||_{C^k(\bar{\Omega})}:=|u|_{k;\Omega}=\sum_{j=0}^{k}[u]_{j;\Omega}
\]
对于\(C^{k,\alpha}(\bar{\Omega})\)函数空间,我们定义其拟范数为:
\[[u]_{k,\alpha;\Omega}:=[D^ku]_{\alpha;\Omega}=\sup_{|\beta|=k}[D^{\beta u}]_{\alpha;\Omega}
\]
以及范数:
\[||u||_{C^{k,\alpha}(\bar{\Omega})}:=|u|_{k;\Omega}+[u]_{k,\alpha;\Omega}
\]
当空间\(\Omega\)是有界集时我们记\(d=\mathrm{diam}\Omega\),此时我们还有与\(||\cdot||\)等价的范数\(||\cdot ||'\).定义为:
\[\|u\|_{C^k(\bar{\Omega})}^{\prime}=|u|_{k ; \Omega}^{\prime}=\sum_{j=0}^k d^j[u]_{j, 0 ; \Omega}=\sum_{j=0}^k d^j\left|D^j u\right|_{0 ; \Omega} ;
\]
和:
\[\begin{aligned}
\|u\|_{C^{k, \alpha}(\bar{\Omega})}^{\prime} & =|u|_{k, \alpha ; \Omega}^{\prime}=|u|_{k ; \Omega}^{\prime}+d^{k+\alpha}[u]_{k, \alpha ; \Omega} \\
& =|u|_{k ; \Omega}^{\prime}+d^{k+\alpha}\left[D^k u\right]_{\alpha ; \Omega}
\end{aligned}
\]
2.Poisson方程的内估计1
下边的一个引理是我们在调和方程已经学习过的:
引理1.设\(f\)在\(\Omega\)中是有界可积的,\(w\)是\(f\)的Newton位势,则\(w\in C^1(\mathbb{R}^n)\),且对任意的\(x\in \Omega\),我们有:
\[\begin{equation}
D_iw(x)=\int_{\Omega}D_i\Gamma(x-y)f(y)dy
\end{equation}
\]
下边的一个引理虽然我们在调和方程中没有学习,但是也不难证明,因此这里我们暂且省略.
引理2:设\(f\)在\(\Omega\)中有界且局部Holder连续(以后我们默认指数为\(\alpha,\)这里\(\alpha\le 1\).),又设\(w\)是\(f\)的Newton位势,则\(w\in C^2(\Omega)\),并且在\(\Omega\)中\(\Delta w=f\).对任意的\(x\in \Omega\),有:
\begin{equation}
D_{ij}w(x)=\int_{\Omega_0}D_{ij}\Gamma(x-y)(f(y)-f(x))dy-f(x)\int_{\partial \Omega_0}D_i\Gamma(x-y)\nu_i(y)dS_y
\end{equation}
其中\(\Omega_0\)是任何一个包含\(\Omega\)的区域,在\(\Omega_0\)上散度定理成立.
下边我们给出关于\(w\)的二阶导数Holder估计.
定理3: 设\(x_0\in \mathbb{R}^n\),记\(B_1=B_R(x_0),B_2=B_{2R}(x_0)\).假设\(f\in C^{\alpha}(\bar{\Omega})\)(以后我们都记\(C^{0,\alpha}\)为\(C^{\alpha}\).如果\(w\)是\(f\)在\(B_2\)的Newton位势,则\(w\in C^{2,\alpha}(\bar{B}_1))\), 并 且 (注意到这里虽然用到\(||\cdot||'\)但是由于\(B_2\)是有界的,因此我们很容易导出对于的\(||\cdot||\)的估计.)
\[\begin{equation}
\left|D^2 w\right|_{0, \alpha ; B_1}^{\prime} \leqslant C|f|_{0, \alpha ; B_2}^{\prime}
\end{equation}
\]
即:
\[\left|D^2 w\right|_{0 ; B_1}+R^\alpha\left[D^2 w\right]_{\alpha ; B_1} \leqslant C\left(|f|_{0 ; B_2}+R^\alpha[f]_{\alpha ; B_2}\right)
\]
证明: 证明的关键:对任意的\(x,\bar{x}\in B_1\),估计:
\[\frac{D_{ij}w(x)-D_{ij}w(\bar{x})}{|x-\bar{x}|^{\alpha}}
\]
再次首先我们注意到:
\[D_iw(x)=\frac{1}{n\omega_n}\cdot \frac{1}{|x-y|^{n-1}},D_{ij}w(x)=\frac{(x_i-y_i)(x_j-y_j)}{w_n|x-y|^n},i\ne j
\]
当\(i \ne j\)时和\(D_{ij}w(x)\)也是同样的阶数,因此利用(4)我们可以得到:
\[\begin{align*}
D_{ij}w(x)=&\int_{B_2}D_{ij}\Gamma(x-y)(f(y)-f(x))dy-f(x)\int_{\partial B_2}D_i\Gamma(x-y)\nu_i(y)dS_y\\
\le &\frac{|f(x)|}{n\omega_n}R^{1-n}\int_{\partial B_2}dS_y+\frac{[f]_{\alpha;x}}{\omega_n}\int_{B_2}|x-y|^{\alpha-n}dy\\
\le& C_1(n,\alpha)(|f(x)+R^{\alpha}[f]_{\alpha;x})
\end{align*}
\]
现在我们计算\(D_{ij}w(x)-D_{ij}w(\bar{x})\).其中主要分为两部分:
第一部分:
\[f(\bar{x})\int_{\partial B_2}D_i\Gamma(\bar{x}-y)\nu_i(y)dS_y-f(x)\int_{\partial B_2}D_i\Gamma(\bar{x}-y)\nu_i(y)dS_y=f(x)I_1+(f(x)-f(\bar{x}))I_2
\]
其中\(I_1,I_2\)分别为:
\[\begin{aligned}
& I_1=\int_{\partial B_2}\left(D_i \Gamma(x-y)-D_i \Gamma(\bar{x}-y)\right) \nu_j(y) d S_y, \\
& I_2=\int_{\partial B_2} D_i \Gamma(\bar{x}-y) \nu_j(y) d S_y,
\end{aligned}
\]
现在我们分别对\(I_1,I_2\)进行估计.对\(I_1\)
\[\begin{align*}
\left|I_1\right| &\leqslant|x-\bar{x}| \int_{\partial B_2}\left|D D_i \Gamma(\hat{x}-y)\right| d S_y \text{对} x \text{和} \bar{x} \text{之间的某点}\hat{x}\\
&\leqslant \frac{C(n)|x-\bar{x}|}{R} \text{因为对} y \in \partial B_2 \text{有 }|\hat{x}-y| \geqslant R\\
&\leqslant \frac{C(n)|x-\bar{x}|}{R}, \text{因为对} y \in \partial B_2 \text{有} |\hat{x}-y| \geqslant R\\
&\leqslant C(n,\alpha)\left(\frac{\delta}{R}\right)^\alpha,\text{ 因为} \delta=|x-\bar{x}|<2 R
\end{align*}
\]
这里死活和[G-T]的估计差个常数,因此干脆用\(C(n)\)表示,不影响后续的估计.
对\(I_2\)直接有:
\[\left|I_2\right| \leqslant \frac{1}{n \omega_n} R^{1-n} \int_{\partial B_2} d s_y=2^{n-1}
\]
现在对\(D_{ij}w(x)-D_{ij}w(\bar{x})\),\textbf{第二部分}分析:
\[\int_{B_2}D_{ij}\Gamma(x-y)(f(y)-f(x))dy-\int_{B_2}D_{ij}\Gamma(\bar{x}-y)(f(y)-f(\bar{x}))dy
\]
我们先将\(B_2\)分为\(B_{\delta}(\xi)+B_2-B_{\delta}(\xi)\),其中:\(\delta=|x-\bar{x}|,\xi=\frac{1}{2}(x+\bar{x})\)
.
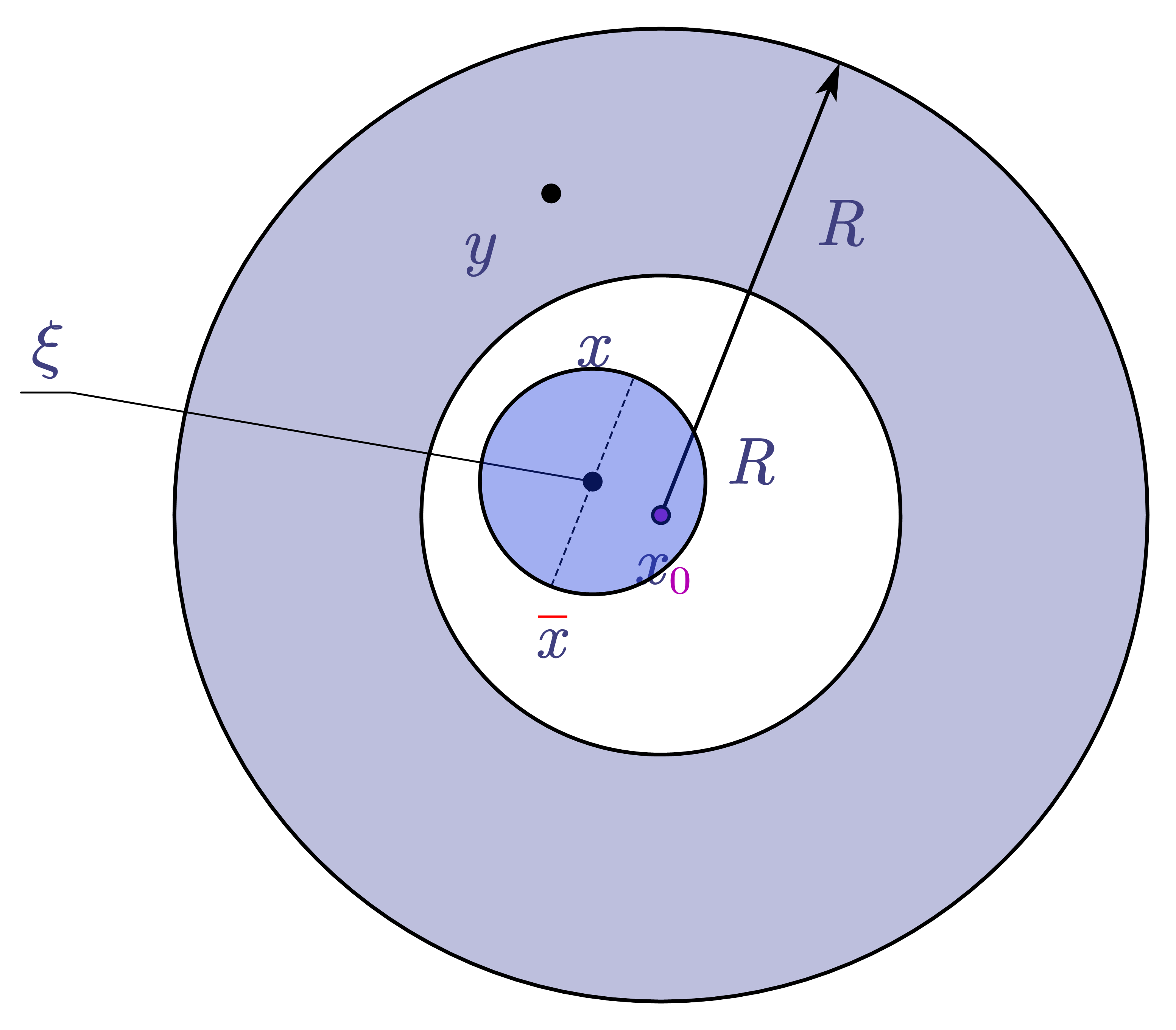
因此第二部分就变成了:
\[\begin{align*}
&\int_{B_\delta(\xi)}D_{ij}\Gamma(x-y)(f(y)-f(x))dy-\int_{B_\delta(\xi)}D_{ij}\Gamma(\bar{x}-y)(f(y)-f(\bar{x}))dy\\ +&\int_{B_2-B_\delta(\xi)}D_{ij}\Gamma(x-y)(f(y)-f(x))dy-\int_{B_2-B_\delta(\xi)}D_{ij}\Gamma(\bar{x}-y)(f(y)-f(\bar{x}))dy\\
=&I_3+I_4+(f(x)-f(\bar{x}))I_5+I_6
\end{align*}
\]
通过简单的拆分,我们可以将前两项写为:
\[\begin{aligned}
& I_3=\int_{B_\delta(\xi)} D_{i j} \Gamma(x-y)(f(x)-f(y)) d y, \\
& I_4=\int_{B_\delta(\xi)} D_{i j} \Gamma(\bar{x}-y)(f(y)-f(\bar{x})) d y,
\end{aligned}
\]
后两项写为:
\[\begin{aligned}
I_5 & =\int_{B_2-B_\delta(\xi)} D_{i j} \Gamma(x-y) d y \\
I_6 & =\int_{B_2-B_\delta(\xi)}\left(D_{i j} \Gamma(x-y)-D_{i j} \Gamma(\bar{x}-y)\right)(f(\bar{x})-f(y)) d y .
\end{aligned}
\]
不同于\(I_1,I_2\)的曲面积分,这里的积分会出现瑕点,因此我们会采用将积分区域分开的方法.
对\(I_3,I_4\)的估计是相同的.
\[\left|I_3\right| \leqslant \int_{B_\delta(\xi)}\left|D_{i j} \Gamma(x-y)\right||f(x)-f(y)| d y
\leqslant \frac{1}{\omega^n}[f]_{\alpha ; x} \int_{B_{3 \delta / 2}(x)}|x-y|^{\alpha-n} d y=\frac{n}{\alpha}\left(\frac{3\delta}{2}\right)^{\alpha}[f]_{\alpha;x}
\]
对\(I_5\)进行估计,利用Gauss-Green公式我们就得到了:
\[\begin{aligned}
\left|I_5\right| & =\left|\int_{\partial\left(B_2-B_\delta(\xi)\right)} D_i \Gamma(x-y) \nu_j(y) d S_y\right| \\
& \leqslant\left|\int_{\partial B_2} D_i \Gamma(x-y) \nu_j(y) d s_y\right|+\left|\int_{\partial B_\delta(\xi)} D_i \Gamma(x-y) \nu_j(y) d S_y\right| \\
& \leqslant 2^{n-1}+\frac{1}{n \omega_n}\left(\frac{\delta}{2}\right)^{1-n} \int_{\partial B_\delta(\xi)} d S_y=2^n .
\end{aligned}
\]
对\(I_6\)进行估计:
\[\begin{aligned}
\left|I_6\right| &\leqslant|x-\bar{x}| \int_{B_2-B_\delta(\xi)}\left|D D_{i j} \Gamma(\hat{x}-y)\right||f(\bar{x})-f(y)| d y \\
& \leqslant c \delta \int_{|y-\xi| \geqslant \delta} \frac{|f(\bar{x})-f(y)|}{|\hat{x}-y|^{n+1}} d y, \quad c=n(n+5) / \omega_n \\
& \leqslant c \delta[f]_{\alpha ; \bar{x}} \int_{|y-\xi| \geqslant \delta} \frac{|\bar{x}-y|^\alpha}{|\hat{x}-y|^{n+1}} d y \\
& \leqslant c\left(\frac{3}{2}\right)^\alpha 2^{n+1} \delta[f]_{\alpha ; \bar{x}} \int_{|y-\xi| \geqslant \delta}|\xi-y|^{\alpha-n-1} d y \\
& \leqslant \frac{c^{\prime}}{1-\alpha} 2^{n+1}\left(\frac{3}{2}\right)^\alpha \delta^\alpha[f]_{\alpha ; \bar{x}}, \quad c^{\prime}=n^2(n+5) . \\
&
\end{aligned}
\]
注意到上个公式的倒数第三行用到了:
\[|\bar{x}-y| \leqslant \frac{3}{2}|\xi-y| \leqslant 3|\hat{x}-y|,
\]
综上所述:
\[\left|D_{i j} w(\bar{x})-D_{i j} w(x)\right| \leqslant C_2\left(R^{-\alpha}|f(x)|+[f]_{\alpha ; x}+[f]_{\alpha ; \bar{x}}\right)|x-\bar{x}|^\alpha
\]
因此我们就得到了结果(再次提醒,这里用到的是\(||\cdot||'\)范数.)
可以从上边的推导中看出,上述的估计中\(C\)只和\(n,\alpha\)有关,这是因为我们采用了\(||\cdot||'\)范数.
另外我们要指出的是虽然上述只出现了\([f]_{\alpha;x}\)或者是\([f]_{\alpha;\bar{x}}\),但是由于Holder拟范数的定义,我们知道这个范数是在\(B_2\)内定义的,因此尽管\(x,\bar{x}\)都在\(B_1\)内,但是Holder拟范数还是用的\([f]_{\alpha;B_2}\)
定理4:设 \(u \in C_0^2\left(\mathbb{R}^n\right), f \in C_0^\alpha\left(\mathbb{R}^n\right)\), 在 \(\mathbb{R}^n\) 中满足 Poisson 方程 \(\Delta u=f\). 那么 \(u \in C_0^{2, \alpha}\left(\mathbb{R}^n\right)\), 并且如果 \(B=B_R\left(x_0\right)\) 是包含 \(u\) 的支集的任一球, 我们就有
\[\begin{equation}
\begin{aligned}
& \left|D^2 u\right|_{0, \alpha ; B}^{\prime} \leqslant C|f|_{0, \alpha ; B}^{\prime}, \quad C=C(n, \alpha), \\
& |u|_{1 ; B}^{\prime} \leqslant C R^2|f|_{0 ; B}, \quad C=C(n) .
\end{aligned}
\end{equation}
\]
证明 :由于\(f\)具有紧支集,因此根据我们调和方程中学到的就知道:
\[u(x)=\int_{\mathbb{R}^n}\Gamma(x-y)f(y)dy
\]
利用引理2和定理3的证明,就可以得到上述估计.
证明: 如果\(f\)不具备紧支集,而是如下形式的Poisson方程:
\[\begin{cases}
\Delta u=f,&x\in \Omega\\ u=g,&x\in \partial \Omega
\end{cases}
\]
则\(w\)不是上述方程的解(需要加一个Green函数有关的积分.)因此我们不能直接得到其内估计,为此我们将方程分为:
\[\begin{cases}
\Delta u_1=0,&x\in \Omega\\ u_1=g,&x\in \partial \Omega
\end{cases},
\begin{cases}
\Delta u_2=f,&x\in \Omega\\ u_2=0,&x\in \partial \Omega
\end{cases}
\]
其中一个调和,一个紧支集在\(\Omega\)内.因此我们利用调和函数的内估计和Newton位势的内估计,就可以得到\(u\)的内估计.
定理5:设\(\Omega\)是\(\mathbb{R}^n\)中的一个区域,\(u\in C^2(\Omega),f\in C^{\alpha}(\Omega)\)在\(\Omega\)中满足Poisson方程\(\Delta u=f\),则\(u\in C^{2,\alpha}(\Omega)\),并且对球\(B_1=B_R(x_0),B_2=B_{2R}(x_0)\subset \subset \Omega\),我们有:
\[ \begin{equation}
|u|_{2, \alpha ; B_1}^{\prime} \leqslant C\left(|u|_{0 ; B_2}+R^2|f|_{0, \alpha ; B_2}^{\prime}\right),
\end{equation}
\]
其中\(C=C(n,\alpha)\).
证明:按照如上所述,我们令:
\[\begin{cases}
\Delta w=0,&x\in \Omega\\ w=u,&x\in \partial \Omega
\end{cases},
\begin{cases}
\Delta v=f,&x\in \Omega\\ v=0,&x\in \partial \Omega
\end{cases}
\]
则\(w=u+v\),因此我们有:
\[\begin{aligned}
& R|D w|_{0 ; B_1}+R^2\left|D^2 w\right|_{0, \alpha ; B_1}^{\prime} \leqslant C R^2|f|_{0, \alpha ; B_2}^{\prime}, \\
& R|D v|_{0 ; B_1}+R^2\left|D^2 v\right|_{0, \alpha ; B_1}^{\prime} \leqslant C|v|_{0 ; B_2} \leqslant C\left(|u|_{0 ; B_2}+R^2|f|_{0 ; B_2}\right) .
\end{aligned}
\]
故得到最终的结论.其中调和函数的内估计为
\[\sup_{\Omega'}|D^{\alpha}u|\le \left(\frac{n|\alpha|}{d}\right)^{|\alpha|}\sup_{\Omega}u
\]
其中\(\Omega'\subset\subset \Omega\).}
