Tasks - AtCoder Regular Contest 149
又是114514年前做的题,现在来写
屯了好多,清一下库存
A - Repdigit Number (atcoder.jp)
直接暴力枚举所有每一位都为\(x\)的数,然后数位从\(1\)到\(n\),若当前枚举到了\(i\),设\(i-1\%M\)为\(now\),则\(now=(now*10+x)\%M\),若\(now\)为\(0\),则\(++cnt\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,m,t;
bool vis[10];
int num,sz;
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=9;++i){
int sur=0;
for(int j=1;j<=n;++j){
sur=(sur*10+i)%m;
if(!sur){
if(j==sz) num=max(num,i);
if(j>sz) sz=j,num=i;
}
}
}
if(!sz) printf("-1");
for(int i=1;i<=sz;++i) printf("%lld",num);
return 0;
}
B - Two LIS Sum (atcoder.jp)
因为\(A_i\)与\(B_i\)是绑定的,所以可以画成几个牌子并且一个牌子分上下两个部分,上半部分为\(A_i\),下半部分为\(B_i\)
因为并没有对操作数目做出限制,所以这个操作实际上就是对\(n\)块牌子随便排序,求\(MAX\{LIS(A)+LIS(B)\}\)
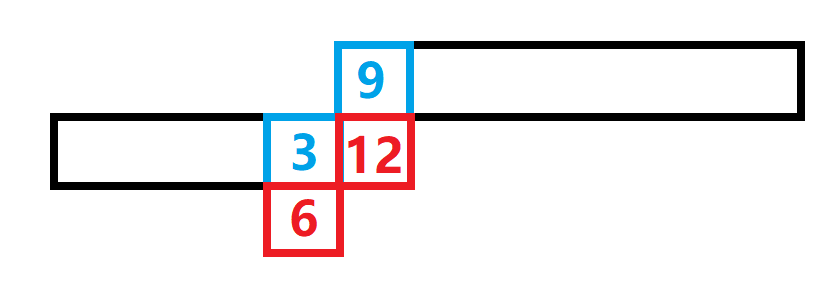
我们可以将\(LIS(A)\)所使用的\(A_i\)和\(LIS(B)\)所使用的\(B_i\)染色,然后就是下图的样子

然后我们可以发现,答案最优时,一定是\(\forall i\),\(A_i\)被染色
- 一块牌子如果没有染色,如果我们想让它的\(A_i\)染上颜色,那么我们可以将这块牌子放到\(A_i\)有染色的牌子\(j\)和\(k\)之间(\(j<k\),且满足\(j\)和\(k\)之间\(\nexists l\),\(A_l\)有染色、\(A_j<A_i<A_k\)),因为\(A\)和\(B\)的值都是全排列,所以如果不存在这样的\(j\)和\(k\),当且仅当\(A_i=1/n\),那么直接将这块牌子放到末尾即可
又因为这块牌子原先没有染色,现在\(A_i\)染了色,且\(B_i\)有可能染色,而且其它牌子的染色情况没有发生变化,所以答案最优时,一定是\(\forall i\),\(A_i\)被染色
- 如果一块牌子原先\(B_i\)有染色,\(A_i\)没有染色,那么还是像\(1.\)一样操作。此时,\(A_i\)被染色,\(B_i\)可能失去染色,也有可能没有,总之整体的染色数量只可能不变或\(+1\),也就是不会亏
所以我们直接将牌子按照\(A\)从小到大排序,因为\(A\)和\(B\)都是全排列,所以现在\(B\)的顺序是固定的,又根据上述证明,直接算出当前\(B\)的\(LIS\)即可
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,ans;
struct node{
int a,b;
bool operator < (const node&other) const{
return a<other.a;
}
}cn[N];
int c[N];
void add(int x,int y){
for(;x<=n;x+=x&-x) c[x]=max(c[x],y);
}
int ask(int x){
int ans=0;
for(;x;x-=x&-x) ans=max(ans,c[x]);
return ans;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&cn[i].a);
for(int i=1;i<=n;++i) scanf("%d",&cn[i].b);
sort(cn+1,cn+n+1),ans=n;
for(int i=1,f;i<=n;++i)
f=ask(cn[i].b)+1,add(cn[i].b,f);
printf("%d",ans+ask(n));
return 0;
}
C - Avoid Prime Sum (atcoder.jp)
因为要求相邻的数相加不是质数,而我们知道,偶数中只有\(2\)是质数且\(2\)不能通过从\([1,+\infty)\)中选两个不同的数相加得到,也就是说,我们可以直接在矩阵的上半部分放奇数,下半部分放偶数
那么对于奇数和偶数相邻的部分,
- 当\(N\%2==0\)时
此时奇数在上面,偶数在下面,而\(奇数*2=偶数\),所以我们在这一排奇数放\(i\in[3,2(N+1)+1](i\%2=1)\),偶数这一排就对应放\(i*2\),他们加起来就是\(3*i\),不是质数
这样放的话只有\(N=4\)的时候会存在放的偶数\(>N*N\)的情况,所以\(4\)直接特判
- 当\(N\%2==1\)时
我们可以发现,这个情况下的奇数和偶数相邻的位置和\(N\%2==0\)的情况类似,只不过会多一个转折,也就是说有一个奇数会和两个偶数相邻
所以我们可以直接找到两个特殊的奇数和两个特殊的偶数,使得将这两个奇数放在转折处,这两个偶数放在这个两个奇数下方可以使得题目的要求成立
经过一番寻找,可以发现有一种方案如图
其它位置按照\(N\%2==0\)的方案放即可
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5;
int n,ans[N][N],now;
bool flag[N*N];
void pt(int x){
printf("%d ",x);
if(++now==n) now=0,printf("\n");
}
int main(){
scanf("%d",&n);
if(n==3) return printf("3 5 1\n9 7 8\n6 2 4"),0;
if(n==4) return printf("15 11 16 12\n13 3 6 9\n14 7 8 1\n4 2 10 5"),0;
if(n&1){
pt(1);
for(int i=(n<<1)+3;i<=n*n;i+=2) pt(i);
pt(9);
for(int i=5;i<=(n<<1)+1;i+=2) if(i!=9) pt(i);
pt(3),pt(12),flag[12]=true;
for(int i=5;i<=(n<<1)+1;i+=2) if(i!=9) pt(i<<1),flag[i<<1]=true;
pt(6),flag[6]=true;
for(int i=2;i<=n*n;i+=2){
if(flag[i]) continue;
pt(i);
}
}else{
pt(1);
for(int i=n+2;i<=n*n/2;++i) pt((i<<1)-1);
for(int i=2;i<=n+1;++i) pt((i<<1)-1);
for(int i=2;i<=n+1;++i) pt((i<<1)-1<<1),flag[(i<<1)-1<<1]=true;
for(int i=2;i<=n*n;i+=2){
if(flag[i]) continue;
pt(i);
}
}
return 0;
}
D - Simultaneous Sugoroku (atcoder.jp)
考虑如果\(X\)为\([1,10^6]\)的全排列,那么我们就可以把\(X\)搬到数轴上去
在某一时刻\(T\),可以发现对于\(X_i=-X_j\),\(i\)和\(j\)的\(X\)值在接下来的任何时刻都是相反数,这给了我们启发
因为\(X\)时全排列,也就是说在\(X\)第一次触碰到负半轴时,整个\(X\)序列一定是跨过原点的连续的一段,这时,我们可以直接将数字数量较少的半轴上的数字\(A_i\)的\(i\)挂到另一个半轴上的数字\(A_j=-A_i\)的\(j\)上,最后输出答案的时候直接将\(j\)的答案取相反数,就是\(i\)的答案
#include<bits/stdc++.h>
#define pii pair<int,int>
#define mp make_pair
#define fi first
#define se second
#define pb push_back
using namespace std;
const int N=3e5+5,MAXN=1e6;
int n,m,x[N],d[N],fa[MAXN+5];
vector<int> edge[MAXN+5];
pii ans[MAXN+5];
void dfs(int x,int depth,int f,int s){
ans[x]=mp(f,s*(depth?-1:1));
for(auto y:edge[x]) dfs(y,depth^1,f,s);
}
int main(){
memset(ans,-1,sizeof(ans));
for(int i=1;i<=MAXN;++i) fa[i]=i;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&x[i]);
for(int i=1;i<=m;++i) scanf("%d",&d[i]);
int l=1,r=MAXN,zero,change=0;
for(int i=1;i<=m;++i){
if(l>r) break;
if(l+change>0) change-=d[i];
else change+=d[i];
zero=-change;
if(zero<l||zero>r) continue;
ans[zero]=mp(1,i);
if(zero-l>=r-zero){
for(int i=zero+1;i<=r;++i) fa[i]=zero*2-i,edge[zero*2-i].pb(i);
r=zero-1;
}else{
for(int i=l;i<zero;++i) fa[i]=zero*2-i,edge[zero*2-i].pb(i);
l=zero+1;
}
}
for(int i=l;i<=r;++i) ans[i]=mp(0,i+change);
for(int i=1;i<=MAXN;++i) if(fa[i]==i) dfs(i,0,ans[i].fi,ans[i].se);
for(int i=1;i<=n;++i){
if(ans[x[i]].fi) printf("Yes %d\n",abs(ans[x[i]].se));
else printf("No %d\n",ans[x[i]].se);
}
return 0;
}
E - Sliding Window Sort (atcoder.jp)
将题目的操作改为有一个大小为\(M-1\)的序列\(S\),其中的元素按从小到大的顺序排列,还有一个大小为\(N-M+1\)的队列\(T\),每次把\(T\)的队首放到\(S\)里去,再把\(S\)的队首放到\(T\)的队尾
然后题目一下就简单起来了,因为我们可以把任何次数操作都转换成\(N-M+1\)次操作
当\(k=N-M+1\)时,最后的答案,也就是题目输入的\(B\),就是把\(S\)接到\(T\)的后面即可
当\(k=N-M+2\)时,\(B_{N-M+2}\)就是将\(B_{N-M+1}\)中\(T\)向前转一个,再将整个\(B_{N-M+1}\)向后转一个
总结一下,大概就是
当\(k<N-M+1\)时,只需要把\(i\in[k+M,N]\)的\(B_i\)(题目中给出的序列)直接甩掉,将\(N\)改成\(k+M-1\)即可
当\(k>N-M+1\)时,\(S\)已经固定了,而\(T\)就是在不断的循环移动,所以可以直接还原到\(k=N-M+1\)时的序列
那么现在我们已经使得\(k=N-M+1\),如果当前情况下\(S\)不为\([N-M+2,N]\)的全排列,则无解;否则,对于\(S\)中的数字,选出它们的方案数为\((M-1)!\)
对于还原后到\(k=N-M+1\)状态下的\(T\),如果\(T_i>T_{i+1}\),说明\(T_{i+1}\)是在选出\(T_i\)后再加入\(S\)并且在选\(T_{i+1}\)时被选出,也就是说\(T_{i+1}\)在放入的一瞬间就被拿出来了,换句话说,\(T_{i+1}\)的位置是唯一确定的;所以我们要求还原后的\(T\)为单调上升的,求出这个单调上升的长度,设初始时\(S\)为\(X\),\(T\)为\(Y\),对于每个\(T_i\),有可能是从\(X\)或\(Y_{[1,i]}\)中取出来的,而选\(T_i\)的时候,已经确定了\(j\in[1,i-1]\)的位置且对于\(k\in(i,N]\)的位置,要么没确定,要么已经固定在了\(Y_k\),所以\(T_i\)可以选的位置的数量为\(M-1+i-(i-1)=M\)
答案就是\((M-1)!*M^{单调上升的长度}\)
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5,MOD=998244353;
int n,m,k,cn[N],a[N],b[N];
queue<int> q;
int power(int x,int y){
int ans=1;
for(;y;y>>=1,x=1ll*x*x%MOD) if(y&1) ans=1ll*ans*x%MOD;
return ans;
}
int get(int x){
int ans=1;
for(int i=2;i<=x;++i) ans=1ll*ans*i%MOD;
return ans;
}
int get(int x,int mod){
if(x%mod==0) return mod;
return x%mod;
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;++i) scanf("%d",&cn[i]);
if(k<n-m+1){
for(int i=1;i<=m+k-1;++i) a[i]=cn[i];
sort(a+1,a+m+k);
for(int i=1;i<=m+k-1;++i) cn[i]=lower_bound(a+1,a+m+k,cn[i])-a;
n=m+k-1;
}
for(int i=1;i<=n;++i) a[i]=cn[get(i+k%n,n)];
for(int i=1;i<m;++i) if(a[i]!=n-m+1+i) return printf("0"),0;
rotate(a+m,a+m+((n-m+1)-(k-(n-m+1))%(n-m+1)),a+n+1);
for(int i=m;i<=n;++i) if(!q.size()||a[i]>q.back()) q.push(a[i]);
printf("%d",1ll*power(m,q.size())*get(m-1)%MOD);
return 0;
}
