会议:ACL,时间:2023,学校:北京航空航天大学,多伦多大学
关键词:基于张量分解;频率注意力;正则化
摘要:
之前基于张量分解的TKGC模型存在仅独立考虑一种关系与一个时间戳的组合,忽略了嵌入的全局性质的问题。
本文的方法:一种频率注意力(FA)模型来捕获一个关系与整个时间戳之间的全局时间依赖性。具体来说,我们使用离散余弦变换(DCT)来捕获时间戳嵌入的频率,并进一步计算频率注意力权重以进行缩放同时,之前的时间塔克分解方法使用简单的范数正则化来约束核心张量,这限制了优化性能。因此,我们提出了核心张量的正交正则化(OR)变体,它可以限制第三个核心张量的非上对角元素。
介绍:
TKGC的关键挑战是如何将时间戳集成到KGC建模中,分为以下四个分支:
1.时间相关嵌入方法(Trivedi et al, 2017; Goel et al, 2020; Dasgupta et al, 2018)将时间信息视为实体或关系的变换或激活函数。
2.时间戳嵌入方法(Han et al, 2021b;Lacroix et al, 2020;Shao et al, 2022)将时间戳视为分数函数的附加可学习嵌入。实验经验表明时间戳嵌入通常比时间相关嵌入表现更好。
3.知识图快照方法(Liao et al, 2021;Li et al, 2021)聚合裁剪子图的多关系交互以实现更精确的表示。
4.历史语境方法(Jung 等人,2021;Zhu 等人,2021)对 n 跳事实链或重复事实进行建模以增加可解释性。
之前的时间戳嵌入方法:每个四元组独立建模,仅捕获局部时间依赖性,忽略一个关系与整个时间戳之间的全局时间依赖性。Tucker分解器被解释为高维线性分类器来区分事实。 TuckERTNT(Shao et al, 2022)使用简单的 L2 范数作为核心张量正则化。然而,这种正则化可能过于严格,导致嵌入急剧变化并存在消失或爆炸的风险。
本文的模型:提出了频率注意力(FA)模型来解决这个问题。具体来说,我们将时间戳嵌入中的每个维度视为长期信号,并使用离散余弦变换(DCT)来捕获信号的频率。此外,我们将关系嵌入的频率和部分作为输入来计算每个时间戳的注意力权重。所提出的频率注意模型可以很容易地应用于现有的张量分解方法。
除此之外,针对正则化问题,本文提出了核心张量的正交正则化(OR)的两种变体,即排除核心张量的每个切片矩阵的上对角元素或对角元素。通过这种方式,我们实现了平衡的核心张量正则化,防止嵌入范数消失或爆炸。
本文的贡献:
1.我们提出了一种使用 DCT 的频率注意模型来捕获关系和整个时间戳之间的全局时间依赖性。
2.我们为tucker分解引入了核心张量正交正则化的两种变体,可以防止嵌入范数消失或爆炸。
3.在三个标准数据集上的实验结果表明,我们的模型在多个指标上优于 SOTA 模型。附加分析证明了我们的频率注意模型和正交正则化的有效性。
相关工作:
静态知识图谱嵌入:
1.基于张量分解的模型 RESCAL(Nickel 等人,2011)、Distmult(Yang 等人,2015)、ComplEx(Trouillon 等人,2016)和 TuckER(Balazevic 等人,2019)计算实域或复域中的三元组得分。
2.基于距离的模型建立在欧几里德或双曲距离的基础上,如 TransE (Bordes et al, 2013)、mainfoldE (Xiao et al, 2016) 和 RotatE (Sun et al, 2019) 所示。 DURA(Zhang et al, 2020)指出基于距离的方法可以被视为具有 L2 正则化的分解方法。
3.基于神经的模型使用卷积网络来捕获 KG 结构信息,如 ConvE 所示(Dettmers et al, 2018)。
4.其他模型从各个领域的各种经验中学习。受强化学习的启发,MultiHopKG(Lin 等人,2018)对 nhop 三元组链进行采样,以计算事实三元组分数并对候选者重新排名。
时间信息集成到现有静态嵌入模型:
1.时间相关的实体嵌入可以显式地模拟实体的动态变化,例如周期性和趋势。众所周知的时间相关实体嵌入是历时嵌入(Goel et al, 2020),它使用正弦函数来表示不同时间粒度上实体演化的频率。
2.时间戳嵌入可以用更少的参数实现类似甚至更好的性能。虽然时间戳嵌入可能会受到时间戳数量不断增加的影响,但也可以通过放大来将时间粒度控制在适当的范围内。 TNTComplEx (Lacroix et al, 2020) 中的进一步分析指出,时间相关关系嵌入可以以较小的计算成本获得与时间相关实体嵌入相当的结果。
3.子图角度的TKGC:随着时间的推移,存在一系列知识图快照/子图,其中包含潜在的多关系交互。 (Liao et al, 2021) 采用基于变分贝叶斯推理的概率实体表示来对实体特征和不确定性进行联合建模。 (Li et al, 2021)在每个子图上采用多层图卷积网络来捕获相邻事实的依赖关系。
4.上下文角度的TKGC:查询与其历史上下文之间的相关性可以用作推理的证据。 (Jung 等人,2021)提出了一种使用图注意力层的多跳推理模型,并发现时间位移比时间戳更能指示推理。 (Zhu et al, 2021)注意到 ICEWS 存储库中 1995 年至 2019 年超过 80% 的事件是重复事件。在这种情况下,他们引入了复制机制来对候选人进行重新排名。
前置知识:
问题定义:
“本文用小写字母表示标量,例如 dr,用花字母表示集合,例如 E,用粗体小写字母表示向量,例如 hi 表示第 i 个实体嵌入。我们使用粗体大写字母 H 表示嵌入矩阵,并使用粗体大写字母 W 表示高阶张量。”
“本文使用 a ⊙ b 表示两个向量或矩阵的 Hadamard(元素级)乘积,a ⊗ b 表示张量外积,[A|B] 表示向量或矩阵串联运算符,|| · ||p 表示向量或张量的 p 范数。”
时间知识图 G 由一组事实 \({{(h_i , r_j , t_k, τ_l)} ⊆ \mathcal{E}\times \mathcal{R}\times \mathcal{E}\times \mathcal{T}}\) 组成,其中 E 是有限实体集,R 是有限关系集,T 是有限关系集时间戳设置。每个四元组\({(h_i , r_j , t_k , τ_l )}\)分别表示在特定时间τl 处从头实体hi 到尾实体tk 的关系rj 。时间知识图使用二进制张量 \({\mathcal{X} =\left\{ 0, 1\right\}^{|E|×|R|×|E|×|T|}}\)来表示相应的四联体是否出现在KG数据集中。 |E|,|R|和|T|分别表示实体、关系和时间戳的数量。
本文的任务是实体预测任务,即通过查询 \({(h_i , r_j , ?, τ_l)}\)或 \({(?, r_j , t_k, τ_l)}\)来预测尾实体或头实体。该问题简化为对一组候选实体进行排序,以选择最有可能使部分四元组成为事实的实体。该问题可以表述为排序问题,学习四元组得分函数 \({\hat{\mathcal{X}}=\left( \mathcal{E} ,\mathcal{R} ,\mathcal{E} ,\mathcal{T} \right) \in \mathbb{R}}\) 对所有候选实体进行排序。
Tucker分解:
在KGC任务重,一个三阶张量\({\mathcal{X}}\)可以分解为核心张量\({\mathcal{W} \in \mathbb{R} ^{D_e\times D_r\times D_e}}\)和实体/关系嵌入矩阵E/R作为因子矩阵。 tucker分解的公式如下:
\({\mathcal{X} =\mathcal{W} \times _1\boldsymbol{E}\times _2\boldsymbol{R}\times _3\boldsymbol{E}=<\mathcal{W} ;\boldsymbol{E},\boldsymbol{R},\boldsymbol{E}>=\sum_{d_1=1}^{D_e}{\sum_{d_2=1}^{D_r}{\sum_{d_3=1}^{D_e}{W_{d_1d_2d_3}\boldsymbol{h}_{:d_1}\otimes \boldsymbol{r}_{:d_2}\otimes \boldsymbol{t}_{:d_3}}}}}\)
\({\times_n}\) 表示张量的 n 模乘积,可以解释为核心张量沿 n 维扩展为矩阵。
为了获得正确的时间戳嵌入 T ,TuckERTNT (Shao et al, 2022) 使用两个关系嵌入 R 和 Rt 来分别捕获时变信息和时不变信息,如下所示:
\({\mathcal{X} =<\mathcal{W} ;\boldsymbol{E},\boldsymbol{R}^t\odot \boldsymbol{T}+\boldsymbol{R} ,\boldsymbol{E}>}\)
不过之前的Tucker方法仍存在如下问题:
首先,代表DE-SimplE频率的可学习参数可能聚集在0附近,影响模型性能(如附录D所示)。其次,TuckERTNT 用 L4 范数的四次方约束核心张量。但是,不能保证核心张量的 n 模乘积性能良好。
模型方法:
本文的模型:TuckER-FA
具体方法:本文将 FA 和 OR 与时间 tucker 分解方法相结合。我们将时间戳嵌入和关系嵌入输入到 FA 模型中以计算频率注意权重,然后对时间戳嵌入进行加权求和并将其与关系嵌入相结合。时间戳增强的关系特征和头/尾实体嵌入组成了tucker分解的因子矩阵。
评分函数:
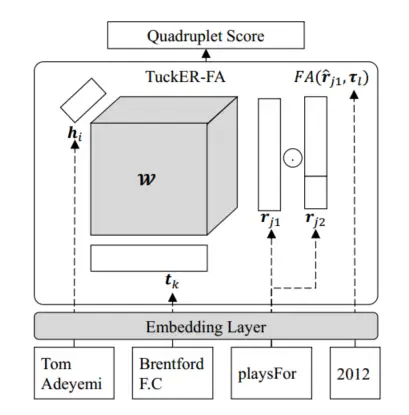
上图展现的是TuckER-FA 的评分函数,可以衡量四元组为真的可能性有多大。灰色部分包含可学习的参数。评分函数公式如下:
\({\mathcal{X} _{ijkl}=<\mathcal{W} ;\boldsymbol{h}_i,\boldsymbol{r}_{j1}\odot \left[ \boldsymbol{r}_{j2}|FA\left( \hat{\boldsymbol{r}}_{j1},\boldsymbol{t}_1 \right) \right] ,\boldsymbol{t}_k>}\)
本文使用\({\rho =\frac{d_{\tau}}{d_r}}\)来控制时间戳和关系之间的嵌入维度比率。\({r_{j1}\in \mathbb{R} ^{d_r},r_{j2}\in \mathbb{R} ^{d_r-d_{\tau}}}\)分别表示两个关系嵌入。\({\tau _l\in \mathbb{R} ^{d_{\tau}}}\)是时间戳嵌入。 FA代表频率注意力模型。\({\hat{\boldsymbol{r}}_{j1}}\)表示与 \({τ_l}\) 对齐的关系嵌入部分。主要计算量集中在tucker分解上而不是FA模型上。
FA模型:
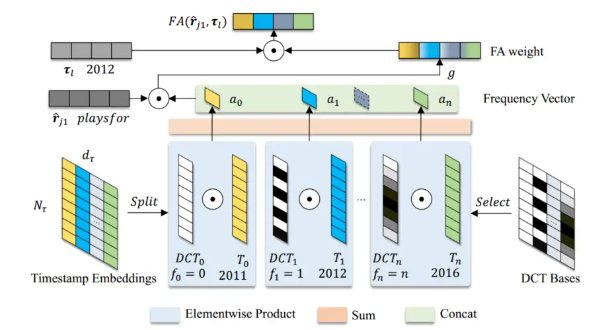
上图为频率注意力(FA)模型的框架,可以捕获一个关系和整个时间戳的全局时间依赖性。这里 g 是一个简单的两层 MLP 加 sigmoid 函数。
本文将时间戳嵌入随时间的演变视为不同频率的周期函数的组合。本文使用离散余弦变换(DCT)来捕获时间戳嵌入的不同频率分量。通过这种方式,本文可以捕获一个关系和整个时间戳的全局时间依赖性。
按时间顺序排列的时间戳嵌入\({\boldsymbol{T}\in \mathbb{R} ^{N_{\tau}\times d_{\tau}}}\)被视为\({d_τ}\)个不同的时间信号。 DCT的直流(DC)分量\({f_0}\)和频率分量\({f_k}\)分别表述如下:
\({f_0=\sum_{i=0}^{N_{\tau}-1}{T_i}=GAP\left( T \right) N_{\tau}}\)
\({f_k=\sum_{i=0}^{N_{\tau}-1}{T_i}\cos \left( \frac{\pi k}{N_{\tau}}\left( i+\frac{1}{2} \right) \right) \,\,k\in \left\{ 0,\cdots \cdots ,N_{\tau}-1 \right\}}\)
GAP代表全局平均池化操作,在计算机视觉领域常用于计算通道注意力权重。在TKGC任务中,直流分量频率注意力的主要计算流程如下:
\({FA\left( \tau _l \right) =\sigma \left( FC\left( GAP\left( T_{:d} \right) N_{\tau} \right) \right) \odot \tau _{:d}}\)
其中FC块代表全连接层,σ表示sigmoid函数。很自然地包含更多的频率分量来计算注意力权重。考虑到计算资源的限制,我们选择性地选择部分频率分量。我们将时间嵌入维度\({d_τ}\)分为 n 个部分,并将一组选定的频率 \({f_0, ...f_n}\) 分配给每个部分。我们还将\({\hat{\boldsymbol{r}}_{j1}}\)引入到FA模型中:
\({FA\left( \hat{\boldsymbol{r}}_{j1},\tau _l \right) =\sigma \left( FC\left( GAP\left( T_{:d} \right) N_{\tau} \right) \right) \odot \tau _{:d}}\)
此外,有限正交函数基运算的计算复杂度是线性的。与Tucker分解的计算成本相比,频率注意力模型的计算成本可以忽略不计。频率注意力权重决定了相应维度的时间戳嵌入信息被保留多少。 FA 模型考虑单个关系在整个时间戳上的演化。
核心张量的正交正则化:
正交正则化使得参数矩阵更加接近对角主导非奇异矩阵。非奇异矩阵可防止矩阵乘法期间特征图突然发生截断变化。此外,Tucker分解可以看作是因子矩阵与核心张量的任意切片的矩阵乘法。换句话说,正交正则化可以应用于核心张量乘法。
本文提出了核心张量正交正则化\({\varPhi _1,\varPhi _2}\)的两种变体。基线是 TuckERTNT 中使用的简单范数正则化\({\varPhi _0}\):
\({\varPhi _0\left( \theta \right) =\left\| \mathcal{W} \right\| _{4}^{4}}\)
\({\varPhi _1\left( \theta \right) =\left\| \mathcal{W} \odot \left( 1-\mathcal{I} \right) \right\| _{4}^{4}}\)
\({\varPhi _2\left( \theta \right) =\left\| \mathcal{W} \odot \left( 1-Proj\left( \mathcal{I} \right) \right) \right\| _{4}^{4}}\)
\({1,\mathcal{I},Proj(\mathcal{I})}\) 是与 W 形状相同的张量。 1 的所有元素均为 1。\({\mathcal{I}}\)的上对角元素为 1,其他元素为 0。\({Proj(\mathcal{I})}\)的任意切片矩阵的对角元素为1,其他元素为0。当核心张量的上对角元素为1,其余元素为0时,tucker分解退化为CP分解。Φ1正则化可以限制tucker 分解到加权 CP 分解的邻域。 核心张量的上对角线元素是权重,其余元素表示与加权CP分解略有不同。
其他正则化:
本文使用嵌入正则化,使用 L4 范数的四次方作为嵌入正则化,来缓解过度拟合问题。
\({\varOmega _4\left( \theta \right) =\left\| \boldsymbol{h} \right\| _{4}^{4}+\left\| \boldsymbol{t} \right\| _{4}^{4}+\left\| \boldsymbol{r}_{\boldsymbol{1}} \right\| _{4}^{4}+\left\| \boldsymbol{r}_2|FA\left( \tau \right) \right\| _{4}^{4}}\)
由于现实世界的时间连续性,很自然地保证嵌入空间中相邻的时间戳嵌入或更接近的重复时间戳嵌入。在计算时间正则化项时,排除此唯一时间戳。为了与嵌入正则化保持一致,相邻时间戳差分正则化如下:
\({\varLambda _4\left( \theta \right) =\frac{1}{|\mathcal{T} |-1}\sum_{i=1}^{|\mathcal{T} |-1}{\left\| \tau _{i+1}-\tau _i \right\| _{4}^{4}}}\)
损失函数:
对于每个训练数据,我们使用瞬时多类损失:
\({\mathcal{L} \left( \mathcal{X} _{ijkl} \right) =-\mathcal{X} _{ijkl}+\log \left( \sum_{k^{\prime}}{\exp \left( \mathcal{X} _{ijk^{\prime}l} \right)} \right)}\)
共同考虑瞬时多类损失和上述三个正则化项,我们通过最小化以下损失函数来训练我们的模型。损失函数如下:
\({\mathcal{L} \left( \mathcal{X} ;\theta \right) =\frac{1}{|S|}\sum_{\left( i,j,k,l \right) \in S}{\left[ \mathcal{L} \left( \mathcal{X} ;\theta \right) +\lambda \varPhi _n\left( \mathcal{X} ;\theta \right) +\lambda _1\varOmega _4\left( \mathcal{X} ;\theta \right) +\lambda _2\varLambda _4\left( \mathcal{X} ;\theta \right) \right]}\,\,n=1,2,3}\)
其中 λ1、λ2 和 λ 是调整的重要超参数。
实验:
前置准备:
三个最常用的数据集来评估我们的模型,包括 ICEWS14、GDELT 和 YAGO15K
评测指标:Hit@k (k ∈ {1, 3, 10}) 和过滤后的平均倒数排名 (MRR)
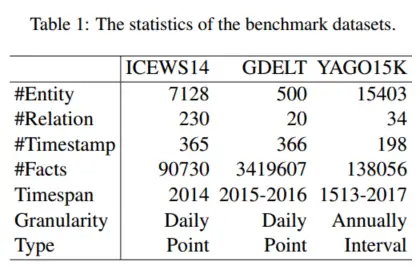
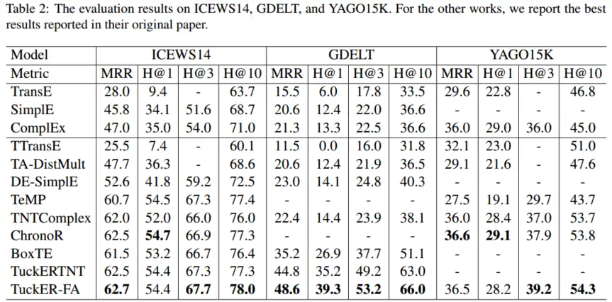
详细结果:
本文的模型在 ICEWS14 和 YAGO3-10 的几个指标上稍微优于或与之前的 SOTA 结果持平。在 GDELT 上,我们的模型在所有指标上都取得了显着的改进结果。与 TuckERTNT 相比,我们的模型 TuckER-FA 有\({d[(1 − ρ)|\mathcal{T}| + (2 + ρ)|\mathcal{R}|]}\)使用相同嵌入维数时,参数更少,MRR 性能提高 1.1%。与 TNTComplex 和 ChronoR 的 2500 多个实体和关系维度相比,我们的模型仅使用 400 个维度的实体和关系就获得了更好的结果。
增加模型参数的数量大大提高了 GDELT 的 MRR 性能,但对其他两个模型的改进很小。与 ICEWS14 相比,GDELT 数据集在相同时间跨度内的事实数量增加了近 38 倍,实体/关系更少。 GDELT 的相应图在空间上更加密集,具有更多重复出现的事实。
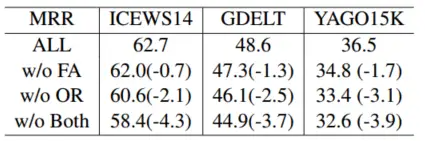
消融实验:
下图显示了频率注意力(FA)模型和核心张量正交正则化(OR)模型的消融研究。可以看出,这两种模型在单独工作时都很有价值,并且它们的组合表现得更好。我们可以指出OR模型比FA模型更有效。
与普通模型相比,单个 FA 模型在 ICEWS14 中显着提高了准确性,这可能是因为该数据集具有最短的时间跨度和最少的数据。 YAGO15K 中单一 OR 模型的改进很小,这可能归因于没有时间戳的事实的存在。
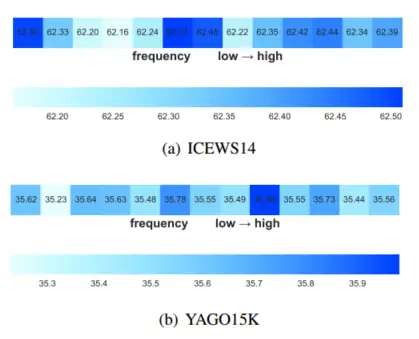
TKG的频率影响:
下图显示了不同单 DCT 基的频率注意力模型的结果。我们使用前六个结果中的频率组合来实现最佳结果。频率之间的差异微不足道,这意味着全局时间依赖性分布在所有频率上。具体来说,直流分量在ICEWS14中是第二高的结果,但在YAGO15K中是第六高的结果。原因可能是YAGO15K中没有时间戳的事实干扰了固有频率的估计。上述结果表明,利用 FA 找到合适的频率特征对于 TKGC 任务是有帮助的。
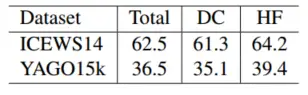
本文计算了整个时间戳内查询 (h, r, ?, ?) 出现的次数。 GDELT 中每个查询的平均出现次数为 284.7,出现多次的查询占训练集的 98.8%。 ICEWS14 的统计结果分别为 7.33、40.8%,YAGO15k 的统计结果分别为 4.51、54.9%。因此,TuckER-FA 在 GDELT 上获得了更好的结果,因为 FA 模块擅长捕获整个时间戳上一个关系之间的全局时间依赖性。
下图显示了 ICEWS14 和 YAGO15k 上两个测试集划分的 MRR 结果。我们将测试集分为两个子集,一个子集由仅出现一次的查询组成(直接流通部件,DC),另一个由出现多次的查询组成(高频组件,HF)。总之,我们的模型在高频分量测试集上效果更好。
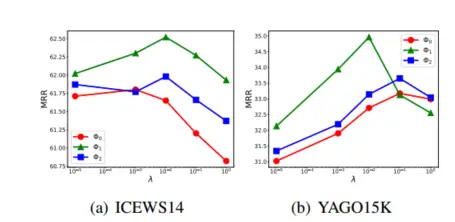
正交正则化:
下图显示了核心张量的三种正则化的详细比较。在本实验中,我们固定 λ1 和 λ2,仅使用直流分量作为频率注意力模型。没有核心张量的任意切片矩阵的对角元素的 Φ2 正则化的性能略好于 Φ0 范数正则化。没有核心张量的上对角线元素的 Φ1 正则化表现最好。
Φ1 正则化使 ICEWS14 上的 MRR 增加 0.7 点,在 YAGO15K 上增加 1.8 点。表现最佳的 Φ1 可以将 ICEWS14 上的 MRR 增加到 2.1 点,在 YAGO15K 上增加 3.1 点。我们可以指出核心张量约束的放松是有效的。
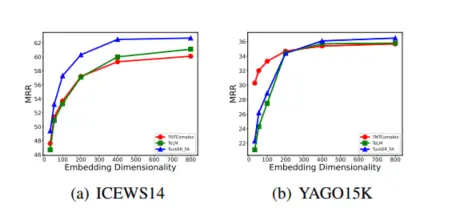
参数复杂性的影响:
下图显示我们的 TuckER-FA 在 ICEWS14 上始终优于具有相同维度的基线 TNTComplEx 和 TeLM。 TNTComplEx 使用专门的矩阵来表示非时间戳嵌入,这使得它在 YAGO15K 上的低维度上表现最佳。我们的 TuckER-FA 可以在高维度上超越。 TeLM的上限没有TuckER-FA那么高。综上所述,我们的模型对于 TKGC 具有最高的性能上限。
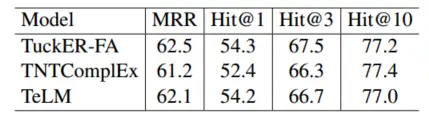
下图显示了在 ICEWS14 上相同参数和 50 个 epoch 训练的比较。我们将可学习参数的大小限制为大约 67M,这意味着 TeLM 的嵌入维数为 2110,TNTComplEX 的嵌入维数为 4000,TuckER-FA 的嵌入维数为 400。我们可以指出,我们的 TuckER-FA 模型在 MRR 和 Hit@3 方面取得了显着的改进,而在其他两个指标方面取得了微弱的改进。
- 时序 图谱 Decomposition Completion Attention时序 图谱decomposition completion 时序 图谱reinforcement attention decomposition attention better matrix 数据库 数据 时序 图谱 时序 图谱 增量embedding-based 时序 图谱correlations relational 时序commonsense-guided图谱commonsense 时序 图谱self-atention hierarchical 时序 图谱 模型 知识 时序 图谱path-memory knowledge