线性代数的知识的有关几何理解
Vector:(向量)
基本含义:
向量相当于为
向量始终起始于原点,并且向量只能是平移。
可以利用坐标系,将分量看成不同的坐标轴所属位置,而构造出向量的空间意义。(向量的分量分别对应着向量空间的坐标轴)
它在线性运算(如:向量相加,向量的数乘)后,更多的表示是,他们在不同分量轴所做的运动距离
单个向量时:
看作一个有方向起于原点的射线。
多个向量时:
将每个向量的方向的终点看作一点(但其本意还是与原点相连)。
表示意义:
此处举例的是二维的基向量的线性运算表示,它所存在于二维空间中,并且它们的所有的a和b值,所得到的结果的集合(集合里可能有:零向量、一维向量(即二维中的一条线)和二维向量的一条线),表示为整个二维空间,这个公式只是简单表示。
基向量:
基向量是线性无关的,不同的基向量可以组成n维空间。n维空间的基向量有n个。
基向量确定了它所在向量空间的方向,当我们根据基向量作坐标系时,我们通过对向量的分量在对应的基向量方向上的投影或刻度,而它们之间的线性组合所得到的向量(矩阵乘向量),就是原向量在经过基向量线性变换后,在新向量空间的位置。
线性相关性
此处我们使用三维空间解释,其中假设有三个向量\(\vec{u}、\vec{v}、\vec{w}\)。
线性相关:
概念:某一个向量是另外两个向量的运算组合。(当它们组成一个方阵时,因为有一行向量的值等于另两行的行线性变换,所以该det|方阵|=0,为奇异矩阵(非满秩矩阵)。再者通过向量间的线性相关的概念也可理解。)
从图形上理解就是:在三维空间(三个基向量组成的空间)中,向量w和v线性运算后的所有线性集合可以组成一个平面,而向量u在前者所组成的平面内,向量u也就表示向量w和v的线性组合。
线性无关:
概念:某一个向量不是另外两个向量的运算组合。(若在同一方阵,则为非奇异矩阵,即满秩矩阵(不被降维),\(\det |A| \neq0\),向量组(矩阵)A可逆)。
从图形上理解就是:假设在三维空间(三维分量组成的空间)中,向量w和v线性运算后的所有线性集合可以组成一个平面,而向量u不在前者所组成的平面内,向量u,向量w和v的线性组合可以表示整个三维空间。
线性变换:
变换:指向量通过线性运算后,是保持网格平行等距变换(运算封闭,原点不变性和基坐标等比例变换):即直线在变换后仍为直线,其向量空间的原点也不会改变。当记住变换后的基向量,那么求其变换后的向量可以根据其进行计算。
在三维空间中,其线性变换类似于二维空间,也是基于基坐标的变换,从而得到在变换后空间中的坐标。
\(Ax\),A表示的是线性变换后的所处空间(或平面)的基坐标,x表示原空间向量,它们相乘之后(也就是以基向量为坐标,根据原点不变性,我们能够根据原向量与变换后基向量相乘就可知变换后坐标),就是x在经过A的列变换之后的坐标(向量:其分量为空间(或平面)的坐标)。
以二维空间举例
\(\left [\begin{array}{cc}\vec{i}&\vec{j} \end{array}\right] \left [\begin{array}{c}x\\y \end{array}\right]=\left [\begin{array}{cc}x \ \vec{i}&y\ \vec{j} \end{array}\right],\vec{i}=\left [\begin{array}{c}a\\c \end{array}\right]\ \vec{j}=\left [\begin{array}{c}b\\d \end{array}\right]\)
x:表示基坐标轴‘i’,y:表示基坐标轴‘j'。
因为向量是从原点进行有向射线的,那么原向量的每个分量就代表它在对应基坐标轴(i或y)上的距离。
解释:
当基坐标进行线性变换之后,因为原点的不变性和向量移动后平面网格的等距性,表示出新基坐标在原向量的基础上与其对应分量值相乘之后,(\(x\vec{i},y\vec{j}\))表示新基坐标的坐标值。
其线性方程组求解,也是利用系数矩阵和常数项(已线性变换后的列向量),求解出未知量向量(即线性变换前的行向量)。
复合变换
线性变换是我们以一个基坐标向量组(一个变换矩阵)乘以向量的视角去看。而复合变换是我们将基坐标进行多次变换(多个变换矩阵)后再去乘以向量(或向量组)来看。
我们先看复合函数的计算:\(f(g(x))\),一般来说我们是先计算里面的\(u=g(x)\),然后再计算外面的\(f(u)\)。而复合变换是\([一个变换矩阵][另一个变换矩阵]x=[一个总的复合变换矩阵]=[x变换后的矩阵]\),根据矩阵乘法我们可以先计算变换矩阵的复合形式,也就是说变换矩阵可以计算成一个总的复合变换矩阵。也就是说我们在以空间的视角去看待复合变换时,我们从右往左(从里往外)将向量依次变换后,所得的向量的最终变换形态与向量经过总复合变换矩阵相乘后得到的形态一致。
个人理解
线性相关性
在n维的向量空间中,线性相关,表示向量组中,具有能够被其他向量表示的向量,也就是具有自由未知量(假设其向量组能表示的空间维数为r:也就是基向量个数为r个),则自由未知量的个数=n-r。线性相关的向量组在经过线性变换后,自由未知量所处的向量会被压缩至零坐标(我们通常称为零空间)。
而线性无关,表示空间中的基向量为n个(也就是向量组的每一个向量都为该空间的一个维度表示)。
线性变换
线性变换的特性:保持网格平行且等距——也就是说,我们在多个向量中,将它们看作一点,并且它们之间可以连接成直线,构建出具有平行线的空间(或平面),当我们进行线性变换时,这些向量会移动到新的位置,当它们重新连接成直线构成空间(或平面)时,你会发现它们遵守了两点:一是距离是等比的;二是原点不变。所以也就对应出该特性——线性变换(对空间的挤压或拉伸)仍保持着网格平行且等距。
向量的分量意义
在一个向量空间中,向量的分量与对应的基向量所在坐标轴对应,而它的分量值代表了在对应坐标轴的刻度或者投影值,通过分量与对应基向量的计算,能够得到它在不同基向量下的投影,将这些投影合起来(一般是向量的加法运算)就可以确定向量在向量空间中的位置和方向。
向量空间(空间上)
解的存在,也表明其常数项列向量能由未知量所组成的列向量线性表示。
从秩来看,当列向量组(矩阵)的秩非满秩时,表明其表示空间(一般为列空间)被压缩于R(秩)维空间。
列空间
其向量线性变换后的所有集合,被称为列空间。
零空间
通俗一点来说,指的是原向量组表示某一维(或某一部分维度)的向量,在空间上被压缩至一点,原此维度方向上的所有方向向量都表示一点。也就是我们说的降维(降秩矩阵)。
即向量组在秩非满秩时,某一部分的向量在线性变换后,压缩至零坐标,则这些向量被称为矩阵的零空间(Null space)或者核(Kernel)。在线性方程组中让常数列向量变为0的解。
零空间的维数是自由未知量的个数(自由未知量个数=未知量个数-其秩)。
向量叉积
得到的是垂直两向量的法向量,右手定则确定法向量方向。
什么是线性
即严格满足运算封闭的空间。(直观理解:网格线保持平行且等距分布)。
运算封闭
可加性:\(L(\vec{v}+\vec{w})=L(\vec{v})+L(\vec{w})\)
成比例:\(L(c\vec{v})=cL(\vec{v})\)
判断向量空间的公理

矩阵和行列式
矩阵乘法
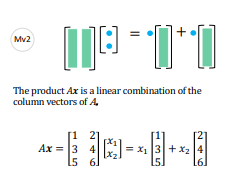
矩阵乘向量
矩阵乘向量就是向量在基向量所处空间的坐标。
\(Ax=0\),表示的是A的列向量与x未知数向量组的线性组合。
\(yA=0\),表示的是A的行向量与y未知数向量组的线性组合
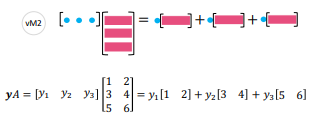
矩阵乘矩阵
首先其几何意义有两种:
复合变换
通过该变换,将改变向量的方向、长度和位置。
向量的坐标变换:
当我们把右矩阵看作是向量组(及内部的列向量表示向量坐标),就是求多个向量在基向量所处空间的对应坐标。
行列式
其空间意义,向量经过线性变换后的空间形体,是其原组成面积(二维)或体积(三维)的定向倍数关系。
注意
当行列式\(det(|n\times n|)=0\)时,我们可知其原方阵不可逆,为奇异(非满秩)矩阵。从而在空间上,表明原方阵可经过线性变换降维
“取向”:也叫翻转。"定向":也叫改变,旋转向指定的方向。
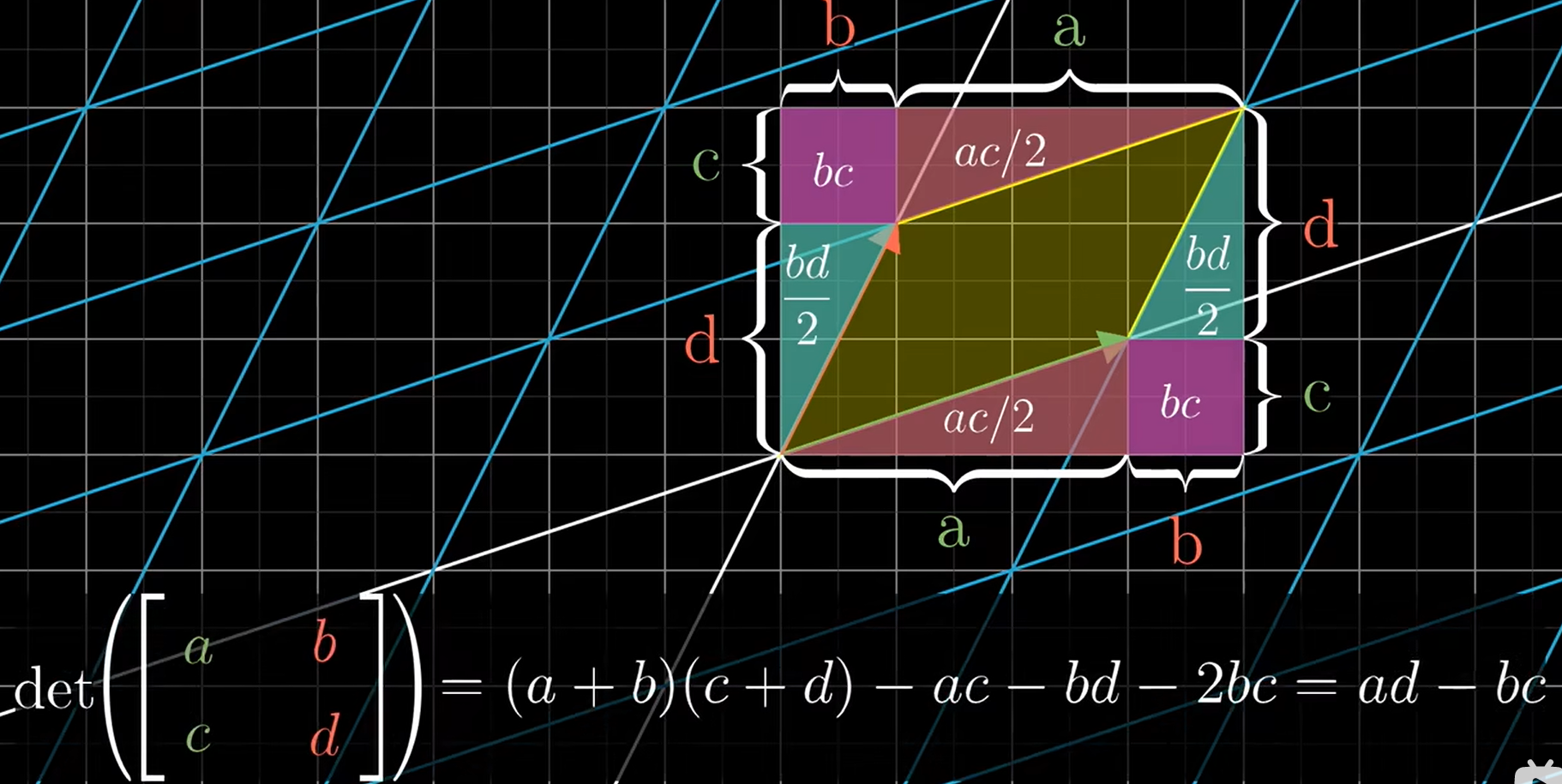
二阶行列式中
其bc有一个为0时,其空间为平行四边形,故bc表示的是ad所构成的四边形对角的拉伸程度。
空间理解
线性代数中的概念应用于函数时的别名
| 线性代数的概念 | 应用函数时的别名 |
|---|---|
| 线性变换 | 线性算子 |
| 点积 | 内积 |
| 特征向量 | 特征函数 |
推荐一个作者所写的文章
以及推荐视频作者:3Blue1Brown和MIT的教授Gilbert Strang's Homepage (mit.edu)
他们所有有关线代的教学视频极大帮助了我在线代学习之路的前进,十分感谢!