526互联

微分方程建模

发布时间 2023-07-23 14:49:46作者: cxy8

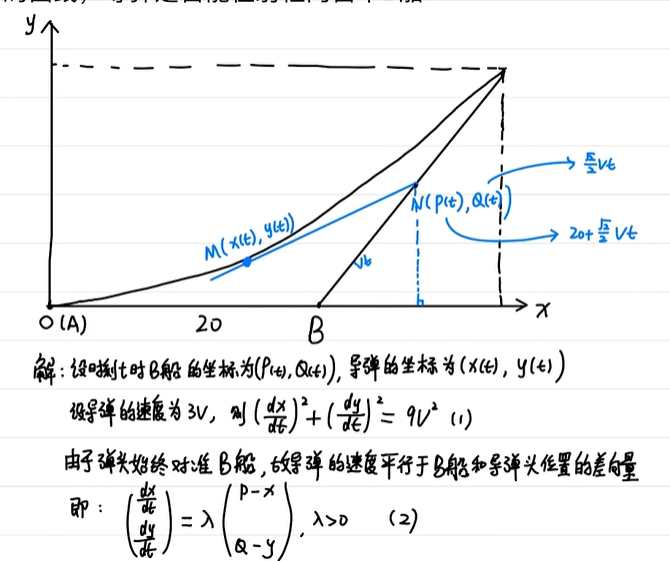
引例

image
3.png
4.png

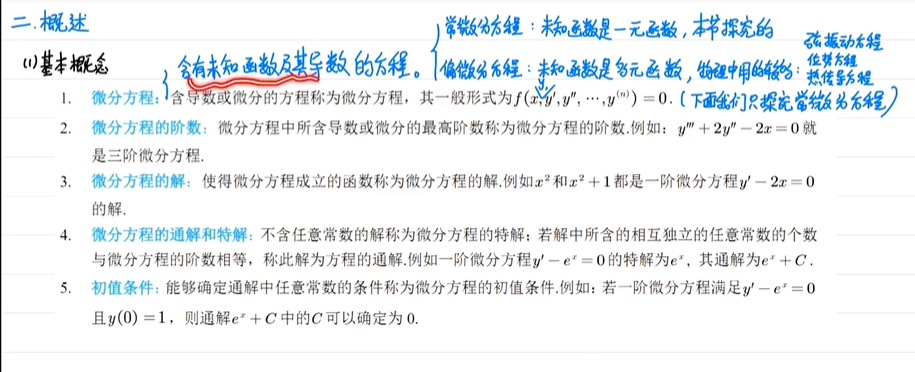
数学概念

5.png

如何建立微分方程

专业知识+套用现有模型

matlab求微分方程解析解

1、解析解：给出解的具体表达式， 数值解：微分方程太复杂了求不出来解析解就只能求数值解
6.png
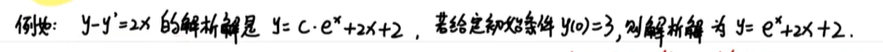
2、matlab求微分方程解的函数

dsolve('方程1', ' 方程2', ..., '方程n ', '初始条件 ', '自变量 ')

注意事项
7.png
eg1；y-dy=2x
ans:

dsolve('y - Dy = 2*x', 'x')

2.png
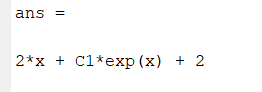
eg2；y-dy=2x 且 y(0) = 3
ans:

%% 注意这里的Dy，其中D是大写
dsolve('y - Dy = 2*x', 'y(0) = 3', x')

这里给出了初始值，与上面eg1的区别是给出初始值求出来的是特解不给的话求出来的是通解
3、关于eg1的拓展，如果微分方程中还含有其他的未知参数如何处理

dsolve('y - Dy = a*x', 'x')

matlab求微分方程数值解

3.png
4.png

ode45和ode15s

刚性和非刚性：
5.png
odee45对应非刚性问题，ode15s对应刚性问题
90%的是用ode45
6.png

clear all;
clc
%% 如果我们觉得每个点之间默认的间隔不够小时，我们可以自己设置
[x, y] = ode45('df1', [0, 2], 3);

%% 画图
figure(1)
plot(x,y, 'b*-');



%% df1.m文件
function dy = df1(x, y)
    % 微分方程y-y'=2x
    dy = y - 2 * x; % 微分方程写成标准形式
    % 注意函数的返回值一定是因变量y的一阶导数
    % 函数的输入有两个，分别是自变量x和因变量y
end

结果图：
7.png
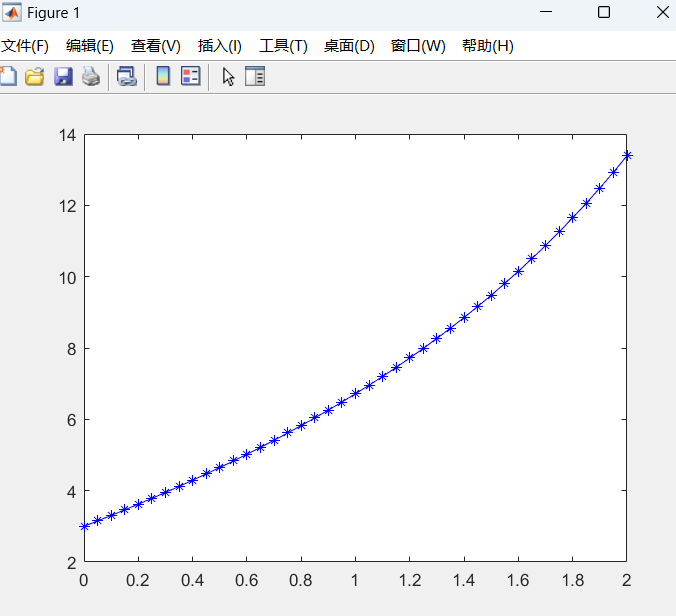
自定义误差版本

clear all;
clc
options = odeset('RelTol', 1e-4, 'AbsTol',1e-8);
[x, y] = ode45('df1', [0, 2], 3, options);

%% 画图
figure(1)
plot(x,y, 'b*-');

例题：
8.png

clear all;
clc
[x, y] = ode45('df2', [0 4 * pi], [0, 1, 1]);

figure(1)
plot(x, y(:, 1), 'b*-')
hold on
plot(x, y(:, 2), 'r.-')
hold on
plot(x, y(:, 3), 'gx-')
% 用来给每个线标注名称
legend('y1', 'y2', 'y3')

%% 微分方程组一定要写成列向量
function dy = df2(x, y)
    dy = zeros(3, 1);
    dy(1) = y(2) * y(3);
    dy(2) = -y(1) * y(3);
    dy(3) = -0.51 * y(1) * y(2);
end

9.png

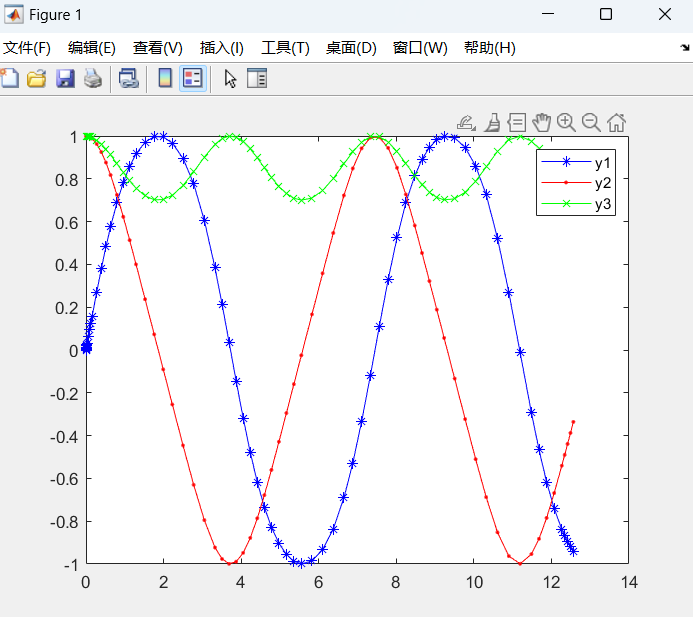
高阶微分方程

10.png