一道初中数学几何题

题目来源：某秃头老师

题面

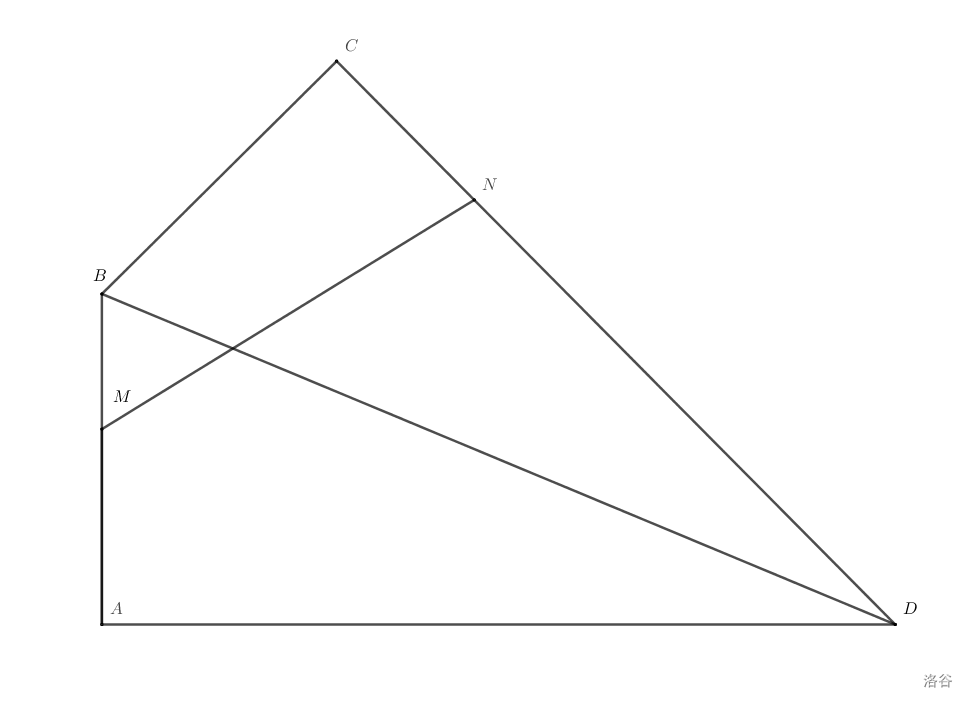
\(\triangle ABD\) 和 \(\triangle CBD\) 是两个全等的直角三角形。其中，\(\angle A = \angle C = 90 ^{\circ}\)，\(AB = CB = 5\)，\(CD = AD = 12\)。\(M\)，\(N\) 分别是线段 \(AB\)，\(CD\) 上的两个动点，且 \(AM = CM\)。连接线段 \(MN\)，求 \(MN\) 的最小值。

解法 #1

\(M\)，\(N\) 两个点都是动点，相互不挨着，这不便于我们思考。考虑把线段 \(AM\) 平移，是它的一个端点与线段 \(AN\) 的一个端点重合。平移的方法或许不是唯一的，而且都可能帮助我们找到答案，下面是其中的一种平移方法：把点 \(M\) 平移到点 \(N\) 上，使得点 \(N\)，\(M\) 重合，点 \(A\) 的对应点为 \(A'\)。

平移后，可以很自然地想到把点 \(A\) 和 \(A'\) 连起来。因为 \(A'N\) 是 \(AM\) 平移过来的线段，所以四边形 \(AMNA'\) 不就是一个平行四边形吗？根据平行四边形的性质，\(MN = AA'\)，这样我们就把要求的线段 \(MN\) 转移到了 \(AA'\) 上。这么转移有一个很大的好处：线段 \(AA'\) 的一个端点 \(A\) 是定点。于是两个动点的问题就变成了一个动点的问题，这无疑方便了我们的思考。

对于动点问题，一个常见的套路是先找出动点的运动轨迹（如果题目中没说的话），这通常会有助于找到答案。而找到运行轨迹通常会和某些定值有关。就拿这道题举例子，如果能证明线段 \(AA'\) 的长度是一个定值，因为点 \(A\) 是定点，那么动点 \(A'\) 的运动轨迹显然就是一个以 \(A\) 为圆心的圆了。或者如果连接点 \(C\) 和 \(A'\)，然后发现 \(\angle DCA\) 等于一个定值 \(\alpha\)，那么 \(A'\) 的运动轨迹就是一条射线。

回到这道题中，我们具体该怎么做呢？事实上，这一步确实比较棘手。它的棘手之处不在于你知道答案之后感到难以理解，其实跟着答案的思路走是很容易理解的。难点在于自己做题时，怎么想出方法？下面我要做几条辅助线，你或许会不理解为什么要这么连接。这种连接方法大概可以说是数学题做多的人的一种直觉，认为这么连接是有用的（其实我上课听老师讲的时候也没有搞懂，老师说“看着就像”）。反正一道题的解题方法往往不是一种，没准这么连就有用呢？如果连了几条辅助线，然后发现一点用都没有，这也是常见的，毕竟做题的过程离不开试错。

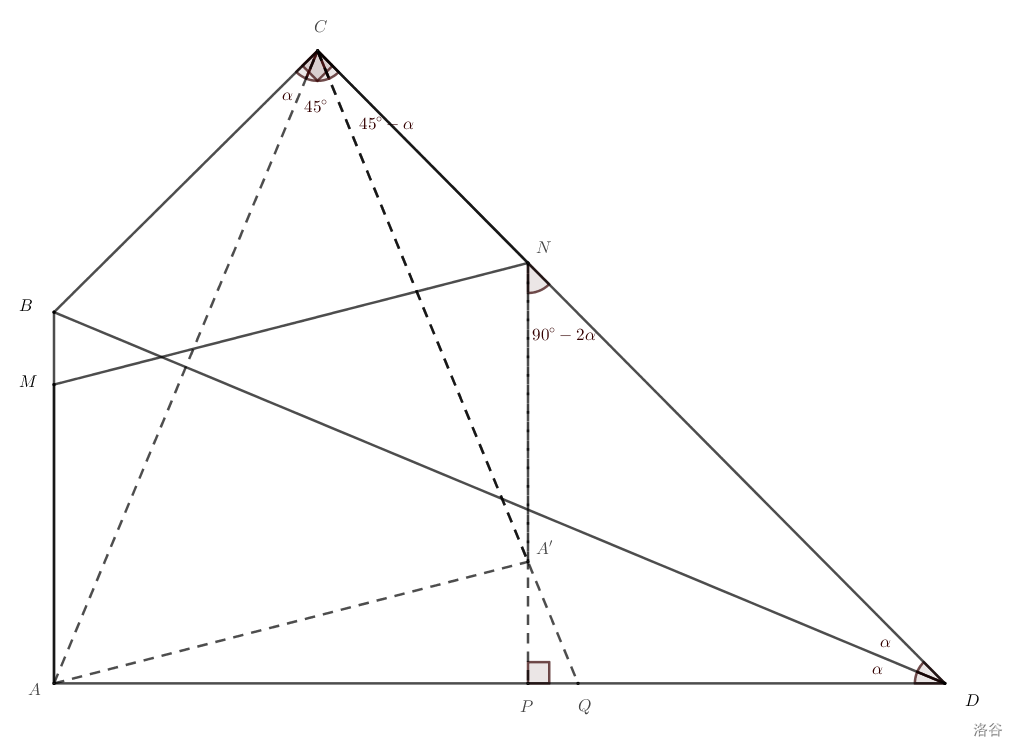
如图，连接线段 \(CA'\)，\(AC\)。延长 \(CA'\) 交线段 \(AD\) 于点 \(Q\)，延长 \(NA\) 交线段 \(AD\) 于点 \(P\)。

设 \(\angle ABD = \alpha\)，则 \(\angle CBD = \alpha\)， \(\angle DNP = 90 ^{\circ} - 2\alpha\)。因为 \(CN = NA'\)，所以 \(\angle DCQ = \angle CA'N\)。又因为 \(\angle DNP\) 是 \(\triangle CNA'\) 的外角，所以 \(\angle DCQ = \dfrac{1}{2} \angle DNP = 45 ^{\circ} - \alpha\)。

\(\triangle ABD\) 和 \(\triangle CBD\) 可以看作是关于直线 \(BD\) 对称的两个三角形，那么线段 \(AC\) 就相当于对称点的连线，所以 \(BD \perp AC\)，进而得到 \(\angle BCR = \alpha\)。

然后我们就发现：\(\angle ACA' = \angle BCD - \angle BCA - \angle DCQ = 90 ^{\circ} - \alpha - (45 ^{\circ} - \alpha) = 45 ^{\circ}\)，这是个定值！也就是说，\(A'\) 在与 \(AC\) 的夹角为 \(45 ^{\circ}\) 的射线上运动！

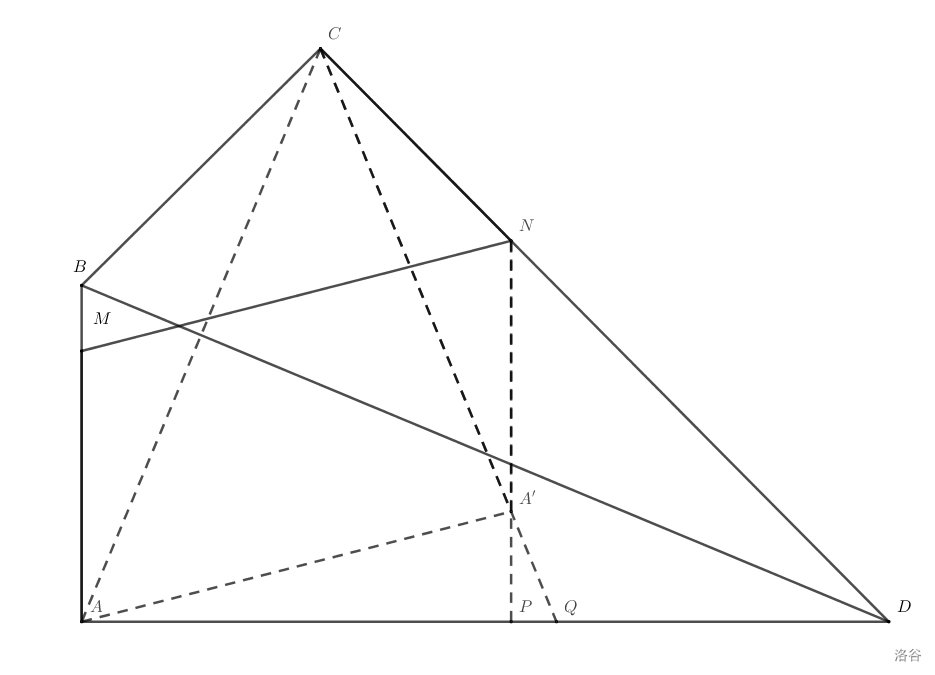
接下来事情就好办了。既然知道 \(A'\) 在一条直线（或者说射线，在这里无所谓）上运动，问题就转化成了求点 \(A\) 到直线 \(CQ\) 的距离，也就是垂线段的长度。下面的步骤就非常常规了，在此只做简要讲解。

根据射影定理，\(AB^{2} = BR \times BD\)，变形得 \(BR =\dfrac{AB^{2}}{BD} =\dfrac{25}{12}\)。根据勾股定理，\(AR = \sqrt{AB^{2} - BR^{2}} = \dfrac{60}{13}\)。因为 \(\angle CAA' = \angle NCA' = 45 ^{\circ}\)，所以 \(AA'' = \sqrt{2}AR = \dfrac{60 \sqrt{2}}{13}\)。

因此，\(MN\) 的最小值为 \(\dfrac{60\sqrt{2}}{13}\)。