本文参考知乎大神明月清风的圆锥曲线一类定点问题研究。
首先给出 Frégier 定理:
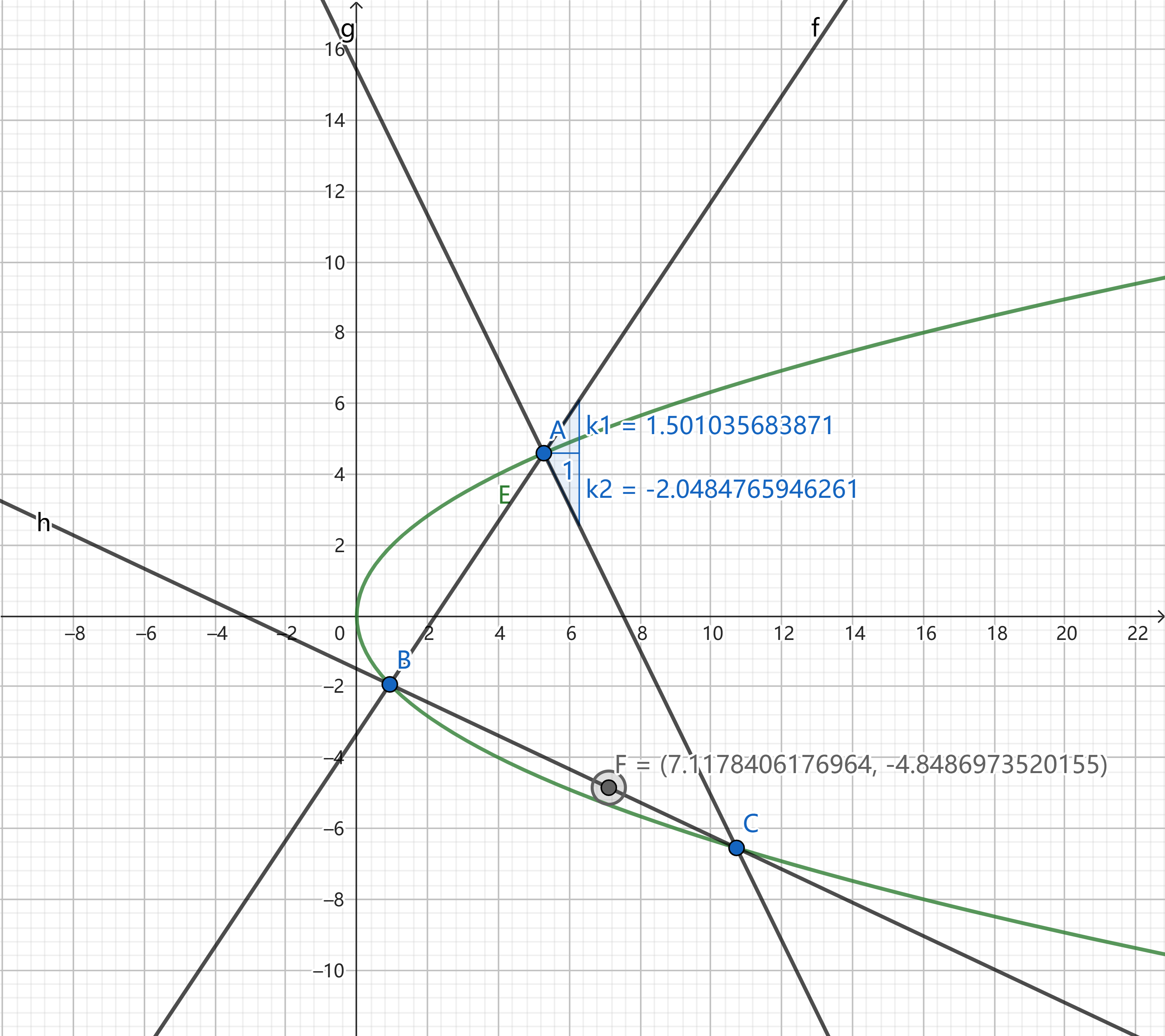
定理(Frégier定理):设有圆锥曲线 \(E\) 及其上一定点 \(P\),设 \(E\) 上两点 \(B,C\) 满足 \(A\) 在以 \(BC\) 为直径的圆上,则直线 \(BC\) 过定点 \(D\),并称该点 \(D\) 为点 \(A\) 关于 \(E\) 的 Frégier 点。
特别地,若 \(BC\) 斜率为定值,那么我们认为其恒过无穷远点。
另外,当 \(A\) 运动时,点 \(D\) 的运动轨迹为与 \(E\) 同心、相似的圆锥曲线。
不难发现这种题在高中圆曲体系里很常见,并且解决方法还挺多样的。
一般可以爆算,齐次化,或者点乘双根。
但更多见的是一类斜率和/积为定值的题目。
这个时候点乘双根就不太合适,选择爆算,齐次化,或者转成极点极线然后用定比点差。
推论:记 \(k_{AB}=k_1,k_{AC}=k_2\)。若 \(\exists\lambda,\mu ,C\in\mathbb{R}\),使得 \(\lambda k_1k_2+\mu(k_1+k_2)=C\) 恒成立,那么直线 \(BC\) 恒过定点 \(D\)。
设 \(A(x_0, y_0)\):
-
对于椭圆 \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\),定点 \(D\) 为 \((x_0+\dfrac{2a^2\mu y_0-2b^2\lambda x_0}{\lambda b^2-Ca^2},y_0+\dfrac{2a^2Cy_0+2b^2\mu x_0}{\lambda b^2-Ca^2})\)。

-
对于双曲线 \(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\),将上式中的 \(b^2\) 换成 \(-b^2\) 即可。

-
对于抛物线 \(y^2=2px\),定点 \(D\) 为 \((x_0-\dfrac{2\lambda p+2\mu y_0}{C},-y_0+\dfrac{2\mu p}{C})\)。