那些分布

二项分布泊松分布几何分布帕斯卡分布
均匀分布指数分布正态分布
它们的参数、概率密度函数与分布函数、统计特征、意义

那些公式

期望

\[E(g(X))=\int_{-\infty}^{+\infty}g(t)f(t)dt. \]

密度函数

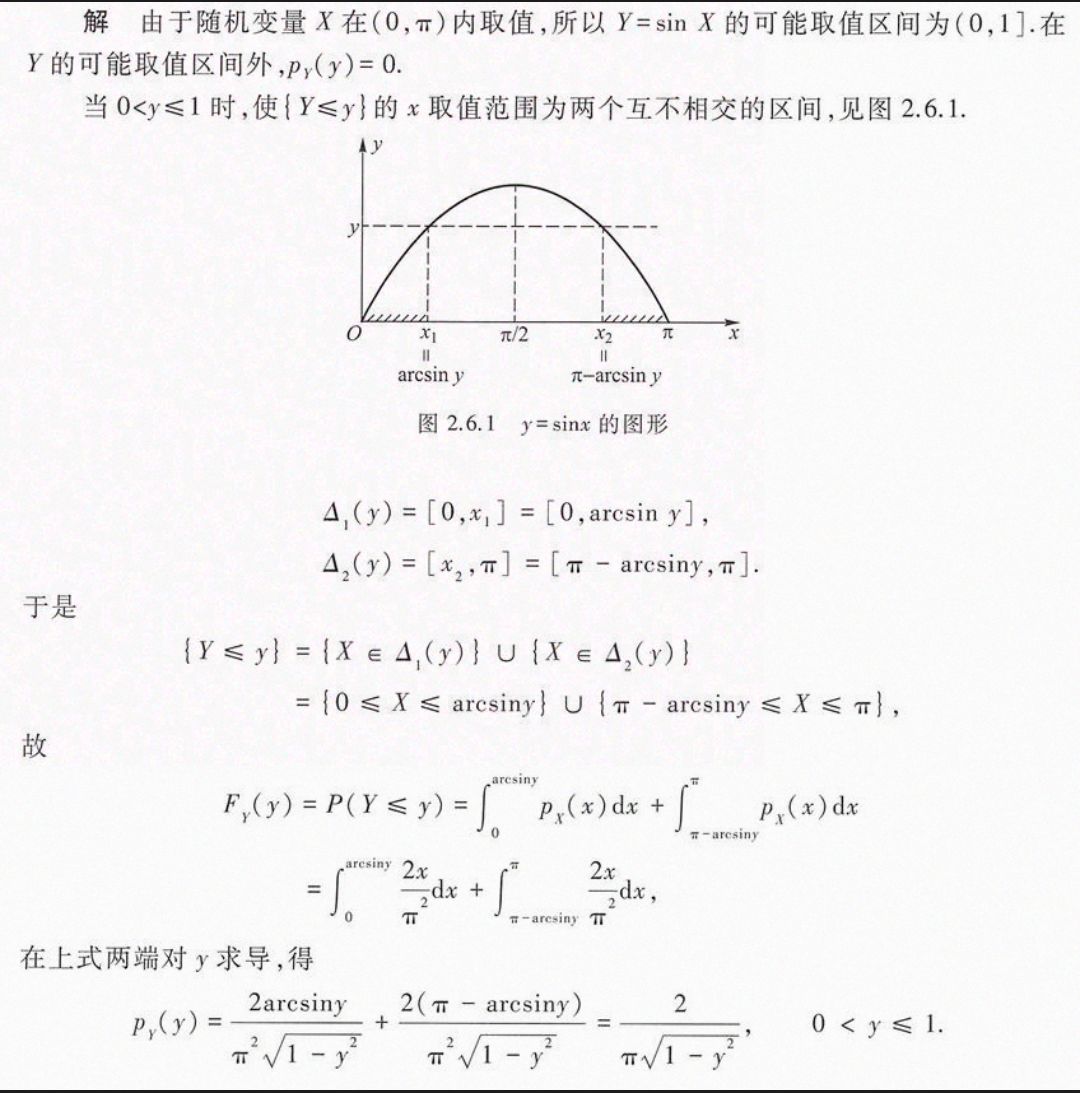
$y=g(x)$处处可导且严格单调，则：
$\begin{gathered} f_Y(y)=\begin{cases}f_X(h(y))|h'(y)|&y\in(\alpha,\beta)\\[2ex]0&\text{其它},\end{cases} \\ \begin{aligned}\text{其中 }\alpha=\min\{g(-\infty),g(+\infty)\}\text{ 和 }\beta=\max\{g(-\infty),g(+\infty)\}.\end{aligned} \\ \end{gathered}$
$\begin{aligned}&\text{可将上述定理推广至区间函数 }x\in[a,b],\text{ 上述定理依旧成立},\text{ 此时有 }\alpha=\min\{g(a),g(b)\}\text{ 和}\\&\beta=\max\{g(a),g(b)\}.\end{aligned}$

上述定理不是万能的。比如下面这题。

那些典

1 匹配问题

和全错排问题等价。
答案是记住了，但是要学会用容斥原理规范地表述呀！

2 蒲丰投针

关键是记住用什么参数去表现针的随机性。一个中点到附近平行线距离，一个夹角。然后几何概型即可。注意应满足 $l<a$

3 十二重计数

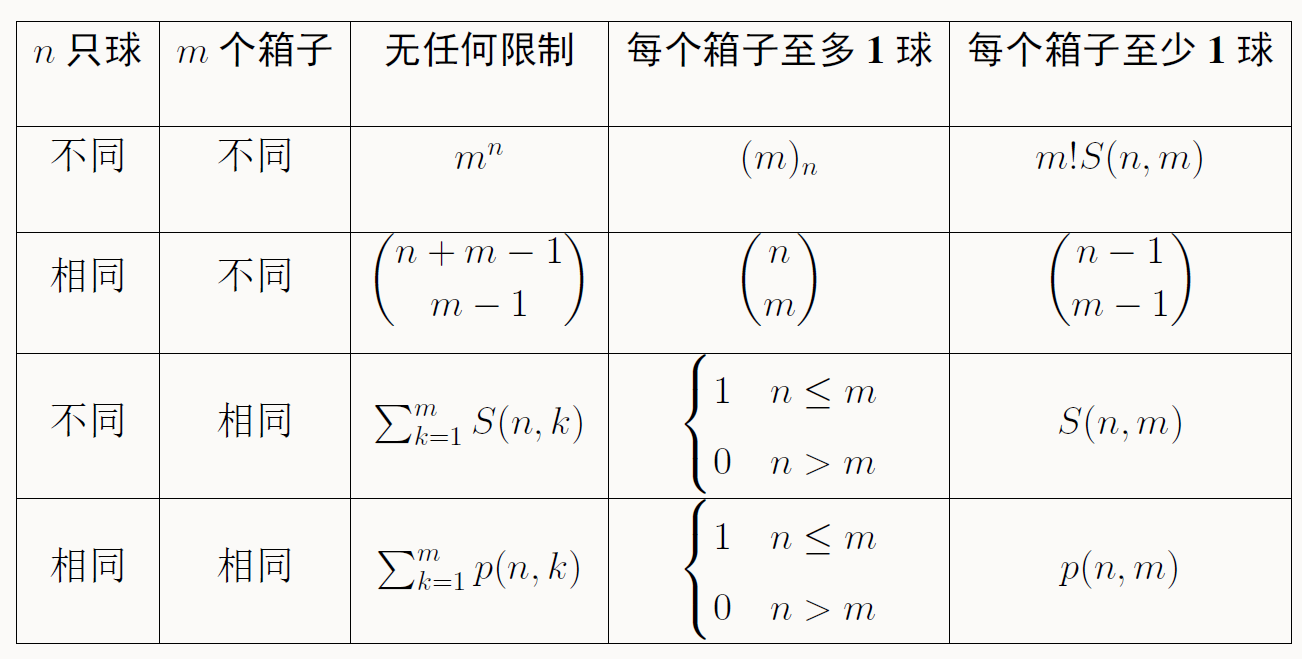
其中，将n 个不同的元素分成m 个非空的子集,不同的划分数称为第二类Stirling 数, 记为S(n,m)
那么有：$$S(n,m) = mS(n − 1,m) + S(n − 1,m − 1)$$
进而归纳可得$S(n,m)=\frac1{m!}\sum_{i=0}^m(-1)^i\binom mi(m-i)^n\quad\text{和}\quad\sum_{m=1}^nS(n,m)(x)_m=x^n.$
注：球同箱子不同每个箱子至多一球的情况写错了。应为$C_m^n$

将正整数n 划分成m 个无序的正整数之和, 不同的划分数记为p(n,m)
则有：

\[\text{对 }n\geq m\geq1,\text{有}\\\begin{cases}p(n,m)=p(n-1,m-1)+p(n-m,m)\\p(n,m)=\sum_{i=1}^mp(n-m,i)\end{cases} \]

4 传球

第一次看到被卡了。。。结果只要考虑某个具体的白球一直没被取到的概率乘以n即可。

5 罐子模型

简单但有趣的模型。

6 啊？

7 经典不等式

\[\operatorname{Var}(X)=E(X-E(X))^2\leqslant E(X-a)^2. \]

\[\operatorname{Var}[X]\leqslant(b-E(X))(E(X)-a)\leqslant(b-a)^2/4. \]

\[对于X\text{~}N(0,1)\text{，有：} \]

\[\begin{aligned}P(X\geqslant\epsilon)\quad&\leqslant\quad\frac12e^{-\epsilon^2/2}\\P(|X|\geqslant\epsilon)\quad&\leqslant\quad\min\left\{1,\sqrt{\frac2\pi}\frac1\epsilon e^{-\epsilon^2/2}\right\}.\end{aligned} \]

后者的证明用到了有趣的$f'(x)=-xf(x)$。
前者公式适合$\epsilon$比较小的情况，后者相反。后者也叫Mill不等式。

8 德国坦克问题

9 集卡问题

集齐n种卡所需要的卡的数量的期望？
用$X_k$表示从有k-1种卡到有k种卡所需要抽卡次数，则$E(X)=\sum E(X_k)$，很容易发现$X_k$服从几何分布
从而求出$E(X)=nH(n)$
回忆：$H(n)\in[\ln(n+1),1+\ln(n)]$

10 随机二叉树叶子结点平均高度

X表示任意给定的一个结点的高度，$X_i$表示第i轮该叶子的祖先是否被选为划分结点，则$X_i=Ber(1/i)$

11 柯西分布

$f(x)=1/\pi(1+x^2)~(x\in\mathbb{R})$
$\begin{aligned}\int_{-\infty}^{+\infty}\frac{|x|}{\pi(1+x^2)}dx=2\int_{0}^{+\infty}\frac x{\pi(1+x^2)}dx=\frac1\pi\left[\ln(1+x^2)\right]_{0}^{+\infty}=+\infty\end{aligned}$
因此柯西分布的期望不存在。
期望的定义要记清楚！有$\text{积分 }\int_{-\infty}^{+\infty}|x|f(x)dx\text{收敛}$的条件！