test

definition

差分约束系统是一种特殊的 \(n\) 元一次不等式组，它包含 \(n\) 个变量 \(x_1,x_2\),\(\dots,x_n\) 以及 \(m\) 个约束条件，每个约束条件是由两个其中的变量做差构成的，形如 \(x_i-x_j\leq c_k\)，其中 \(1 \leq i\), \(j \leq n\), \(i \neq j\), \(1 \leq k \leq m\) 并且 \(c_k\) 是常数（可以是非负数，也可以是负数）。我们要解决的问题是：求一组解 \(x_1=a_1,x_2=a_2,\dots,x_n=a_n\)，使得所有的约束条件得到满足，否则判断出无解。

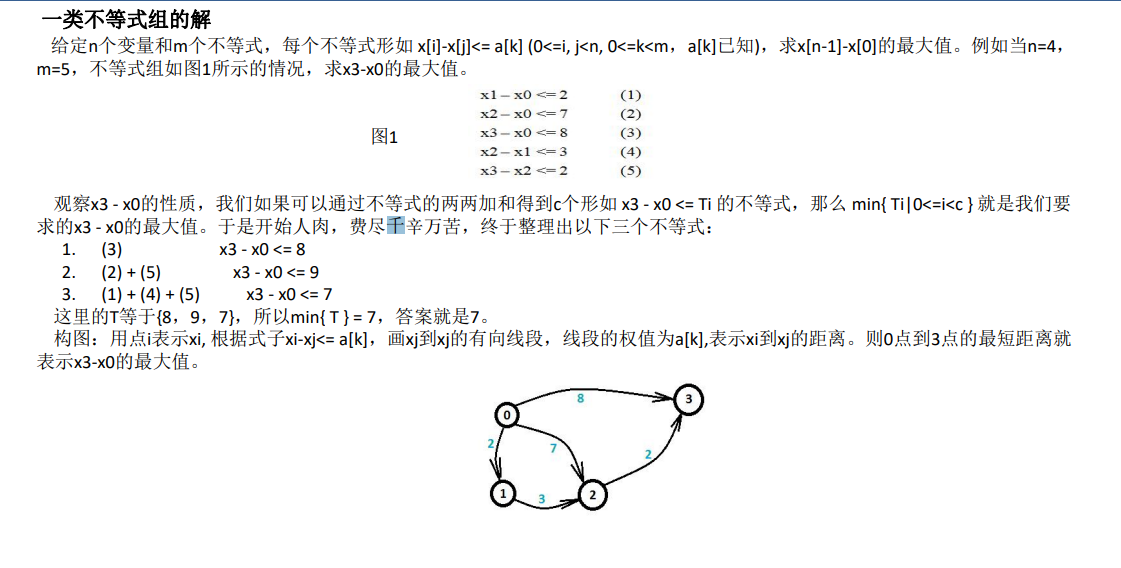
差分约束系统中的每个约束条件 \(x_i-x_j\leq c_k\) 都可以变形成 \(x_i\leq x_j+c_k\)，这与单源最短路中的三角形不等式 \(dist[y]\leq dist[x]+z\) 非常相似。因此，我们可以把每个变量 \(x_i\) 看做图中的一个结点，对于每个约束条件 \(x_i-x_j\leq c_k\)，从结点 \(j\) 向结点 \(i\) 连一条长度为 \(c_k\) 的有向边。

注意到，如果 \(\{a_1,a_2,\dots,a_n\}\) 是该差分约束系统的一组解，那么对于任意的常数 \(d\)，\(\{a_1+d,a_2+d,\dots,a_n+d\}\) 显然也是该差分约束系统的一组解，因为这样做差后 \(d\) 刚好被消掉。

process

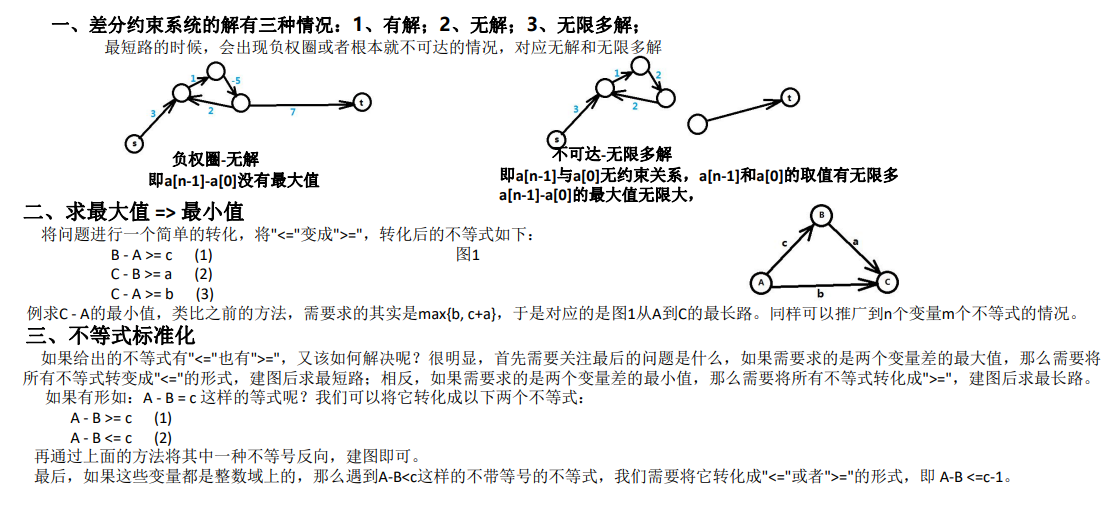
设 \(dist[0]=0\) 并向每一个点连一条权重为 \(0\) 边，跑单源最短路，若图中存在负环，则给定的差分约束系统无解，否则，\(x_i=dist[i]\) 为该差分约束系统的一组解。

properties

一般使用 \(Bellman–Ford\) 或队列优化的 \(Bellman–Ford\)（俗称 \(SPFA\)，在某些随机图跑得很快）判断图中是否存在负环，最坏时间复杂度为 \(O(nm)\)。

in common use

例题 luogu \(P1993\) 小 \(K\) 的农场
 accoders \(P4615\) 小 \(K\) 的农场

题意	转化	连边
\(x_a - x_b \geq c\)	\(x_b - x_a \leq\)	\(add(a, b, -c);\)
\(x_a - x_b \leq c\)	\(x_a - x_b \leq c\)	\(add(b, a, c);\)
\(x_a = x_b\)	\(x_a - x_b \leq 0, \space x_b - x_a \leq 0\)	\(add(b, a, 0), add(a, b, 0);\)

跑判断负环，如果不存在负环，输出 \(Yes\)，否则输出 \(No\)。

Reference code

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;

struct edge {
  int v, w, next;
} e[40005];

int head[10005], vis[10005], tot[10005], cnt;
long long ans, dist[10005];
queue<int> q;

void addedge(int u, int v, int w) {  // 加边
  e[++cnt].v = v;
  e[cnt].w = w;
  e[cnt].next = head[u];
  head[u] = cnt;
}

int main() {
  int n, m;
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= m; i++) {
    int op, x, y, z;
    scanf("%d", &op);
    if (op == 1) {
      scanf("%d%d%d", &x, &y, &z);
      addedge(y, x, z);
    } else if (op == 2) {
      scanf("%d%d%d", &x, &y, &z);
      addedge(x, y, -z);
    } else {
      scanf("%d%d", &x, &y);
      addedge(x, y, 0);
      addedge(y, x, 0);
    }
  }
  for (int i = 1; i <= n; i++) addedge(0, i, 0);
  memset(dist, -0x3f, sizeof(dist));
  dist[0] = 0;
  vis[0] = 1;
  q.push(0);
  while (!q.empty()) {  // 判负环，看上面的
    int cur = q.front();
    q.pop();
    vis[cur] = 0;
    for (int i = head[cur]; i; i = e[i].next)
      if (dist[cur] + e[i].w > dist[e[i].v]) {
        dist[e[i].v] = dist[cur] + e[i].w;
        if (!vis[e[i].v]) {
          vis[e[i].v] = 1;
          q.push(e[i].v);
          tot[e[i].v]++;
          if (tot[e[i].v] >= n) {
            puts("No");
            return 0;
          }
        }
      }
  }
  puts("Yes");
  return 0;
}

\(Bellman–Ford\) 判负环代码实现

下面是用 \(Bellman–Ford\) 算法判断图中是否存在负环的代码实现，请在调用前先保证图是连通的。

bool Bellman_Ford() {
  for (int i = 0; i < n; i++) {
    bool jud = false;
    for (int j = 1; j <= n; j++)
      for (int k = h[j]; ~k; k = nxt[k])
        if (dist[j] > dist[p[k]] + w[k])
          dist[j] = dist[p[k]] + w[k], jud = true;
    if (!jud) break;
  }
  for (int i = 1; i <= n; i++)
    for (int j = h[i]; ~j; j = nxt[j])
      if (dist[i] > dist[p[j]] + w[j]) return false;
  return true;
}