定义式
导数不是用来测量瞬时变化率的,而是测量瞬时变化率的最佳近似。\(\Delta x\) 再小也是存在的,它也是一段变化量。
常见导数:
不常见的:
运算法则
这个就是复合函数的导数,举个例子。
遵循一个链式法则,把里面换个元,逐层分解即可。再来个例子
导数和函数单调性
好神奇。
给个例子。
运用初中知识,易知 \(x < 1\) 时单调递减,\(x > 1\) 时单调递增。
我们考虑导数的几何意义:反映了函数图像上一个点的斜率。我们给 \(f(x)\) 求个导看看:
在 \(x > 1\) 时,\(f^{'}(x) > 0\) ,这就代表着 \(f(x)\) 在 \(x>1\) 的时候是单调递增的;同样的,在 \(x < 1\) 时,\(f^{'}(x) < 0\) ,这就代表着 \(f(x)\) 在 \(x < 1\) 的时候是单调递减的;而当 \(x=1\) 的时候 \(f^{'}(x)=0\) ,说明该处斜率为 \(0\) ,是个拐点。
有了这个,我们就可以很快速的判断单调性和拐点等问题了/oh。
还有,当 \(f^{'}(x) > 0\) 时,\(f^{'}(x)\) 越大,函数增得越快;同理,当 \(f^{'}(x) < 0\) 时,\(f^{'}(x)\) 越小,函数降得越快。
极值与最值
极大值与极小值
来个例子
导一下
这是 \(f(x)\) 的图像
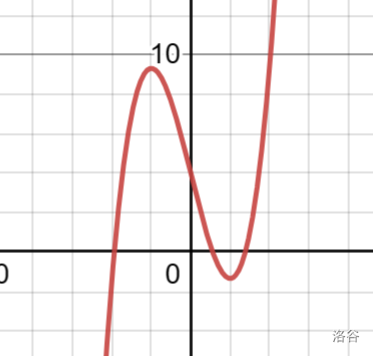
由导数我们可以知道,当 \(x\in(-\infty,-2)\) 时,\(f^{'}(x) > 0\),函数单调递增;当 \(x\in[-2,2]\) 时,\(f^{'}(x) < 0\),函数单调递减;当 \(x\in(2,\infty)\) 时,\(f^{'}(x) > 0\),函数又单调递增。
这里出现了两个极值点:\(-2\) 和 \(2\)。
极值点就是导数为 \(0\) 的点的横坐标。这些点就是所说的拐点,它左边和右边的单调性是相反的。
这里,\(-2\) 是极大值点,\(f(-2)\) 的值比它的邻域的值都要大;\(2\) 是极小值点,\(f(2)\) 的值比它的邻域的值都要小。
同时,\(f(-2)\) 就被称为极大值,\(f(2)\) 就被称为极小值。
最值
\(x\in [a,b]\) 的最值只会出现在两种地方:极值点和端点。因此求导一下,看看是最小值点还是最大值点,再按照题意操作一番就完事了。
洛必达法则
什么都洛只会害了你。
内容
当 \(x \rightarrow t\) 时,\(f(x)\) 与 \(g(x)\) 同时趋近于 \(0\),
则
当 \(x \rightarrow +\infty\) 时,\(f(x)\) 与 \(g(x)\) 同时趋近于 \(+\infty\),
则
给道例题感觉一下。
对任意 \(x>0\) ,有 \((x+1)\ln(x+1) > ax\) 恒成立,则 \(a\) 的范围是_____
很自然的给它分个参
设
,那么我们只需要求这个函数的最小值即可。
最小值怎么求?导一下。最小值怎么求?导一下。
这玩意也很难看单调性啊,怎么办?导一下。怎么办?导一下。
令 \(h(x) = x-\ln(x+1)\)
则 \(h^{'}(x)= 1 - \frac{1}{x+1}\)
当 \(x>0\) 时,\(h^{'}(x)\) 恒 \(>0\),所以 \(h(x)\) 在 \(x>0\) 上是单调递增的,当 \(x=0\) 时,\(h(x) = 0\),这就说明了 \(f^{'}(x)\) 在 \(x>0\) 的时候也是恒 \(>0\) 的,这就又说明 \(f(x)\) 在 \(x>0\) 范围内单调递增。那么最小值就在 \(x=0\) 的时候取得。
因此 \(a\leq f(0)\) 即可,但是 \(f(0)\) 的时候这个式子是无解的啊,怎么办?洛一下。怎么办?洛一下。
设 \(m = f(0)\) ,则有
当 \(x=0\) 时,
,说明上下都是趋于 \(0\) 的。
应用洛必达法则,得:
这时候 \(x=0\) 就是有意义的了,答案就是 \(1\),所以 \(a \leq 1\)。
高考大题好像不让用,但是选择填空可以用/cy。但是不知道这玩意在 OI 中有没有用,觉得好玩,故记之。
帕德逼近
这又是什么黑科技,记一波。
往后面差值就比较大了。
麦克劳林公式
本质是泰勒公式在 \(x=0\) 的一种特殊情况。
本质上就是高阶导数和多项式的一一对应,求一个最近似的多项式函数。
真正的泰勒公式
取 \(f(x-a)\) 的目的就是做一个近似,应该就是发生了一个位移用 \(f(x-a)\) 来近似。
黑科技。
当 \(x \rightarrow 0\) 时,一般就是 \(|x| \leq 0.1\) ,则有
这个就好理解了,美丽的 \(e^x\) 几阶导都是它自己,因此当 \(x\rightarrow 0\) 时,套入公式,十分美丽。
级数:以 \(\cos x\) 为例,如果我们让上式推广到无限项,这无限多项的和,就叫做级数(series)。
收敛和发散:如果一个级数加的越多,它的和越接近某个确定的数值的话,,我们就可以说这个级数收敛到那个值,也就是说这个级数就等于它收敛到的值;反之,如果加的越多,级数不接近任何值,就称这个级数时发散的。
收敛半径:把在用来近似那个点(比如在 \(x=1\) 的时候用一个多项式近似 \(\ln 1\))周围,能够让多项式收敛的最大取值范围,就叫做这个级数的收敛半径。
拉格朗日定理
感觉是求导比斜率,把割线问题转化成切线,也就是导数问题。
两点之间的平均斜率就是两点之间的斜率。
具体可以看这个视频。
又一个黑科技。
定积分
微分是割线的斜率,导数是切线的斜率,当\(\Delta x \rightarrow 0\) 时,它们就是相等的。
导数:是指函数在某一点处变化率的最佳近似。
微分:是指函数在某一点处(趋近于无穷小)的变化量,是一种变化的量
定义
\(f(x)\) 定义在 \([a,b]\) ,任分 \([a,b]\) 为小区间点,分点 \(a=x_0 < x_1 < \dots < x_n = b\) ,这称为 \([a,b]\) 的一个分割。
若 \(\exists \ I \in \mathbb{R}\) ,对 \([a,b]\) 的所有分割都有
则称 \(f(x)\) 在 \([a,b]\) 可积。
\(I\) 称为 \(f(x)\) 在 \([a,b]\) 的定积分,记作
可积的条件
两种情况都可
-
(1):连续必可积
-
(2):有界且存在有限个第一类间断点
微积分基本定理
神。
这个说明的是导数和积分其实是互逆的。
积分后再求导得到的是原函数。
求导后再积分得到的是全体原函数(有常数)。
下面这个就是牛顿-莱布尼茨公式。其中 \(F(x)\) 表示的是 \(f(x)\) 的原函数,\(F(x)\) 的导数是 \(f(x)\)。
举个例子 \(f(x) = x^2\) ,那么 \(F(x) = \frac{1}{3}x^3 + d\) ,但是 \(F(b) - F(a)\) 后 常数项就消没了。
自适应辛普森积分
花了两天学你的前置知识。
首先看 3b1b 的视频我们能得出一个小公式。
\(\text{一段函数的平均高度} = \frac{\text{面积}}{\text{宽度}}\)
其中的面积就用积分求。
辛普森公式
用来解决二次函数的定积分。
对二次函数 \(f(x) = ax^2 + bx + c\) 在区间 \([l,r]\) 上求定积分,而一阶定积分的几何意义就是图像与 \(x\) 轴围成的面积。
求 \(f(x)\) 的原函数:
运用牛顿-莱布尼茨公式:
这就是区间宽度 \(\times\) 平均高度。
自适应辛普森积分法
它的原理是把可积函数分成很多段,每段就可以用二次函数来拟合,也就是把这一段用二次函数来拟合(感觉跟泰勒展开很相似,不过泰勒展开是多项式),套用辛普森公式进行近似计算。
不过这个误差可能会比较大,what should we do?二分。每次判断当前段和二次函数的相似程度,如果足够相似就直接代辛普森公式计算即可,否则将当前段分割成左右两段递归求解。
如何判断当前段和二次函数是否相似?把整段带入公式求一下积分,再将当前段分成左右两端分别代入公式求一下积分。如果当前段的积分和分割后两端的积分相差很小,就可以认为当前段和二次函数是相似的,不用递归分割了。
代码也很简单。
const double eps = ;
double a,b,c,d,l,r;
il double f(double x) { ... }//题目中给出的函数
il double Simpson(double l,double r) { return (r-l)*(f(l)+f(r)+4*(f((l+r)/2)))/6; }//辛普森公式
il double Adaptive_Simpson(double l,double r,double ans)//分治思想
{
double m = (l+r) / 2.0 , a = Simpson(l,m) , b = Simpson(m,r);
if(fabs(a+b-ans) < eps) return ans;
else return Adaptive_Simpson(l,m,a) + Adaptive_Simpson(m,r,b);
}
signed main()
{
scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
printf("%.6lf",Adaptive_Simpson(l,r,Simpson(l,r)));
return 0;
}
为了精确,我们要将 eps 设小一点,往往是 eps = 1e-10。
由此可以看出,这个算法的复杂度是 \(O(\log \frac{n}{\text{eps}})\) ,其中 \(n\) 代表的是积分的上限\(-\)下限,也就是 \(r-l\)。