二项式定理和杨辉三角-526互联

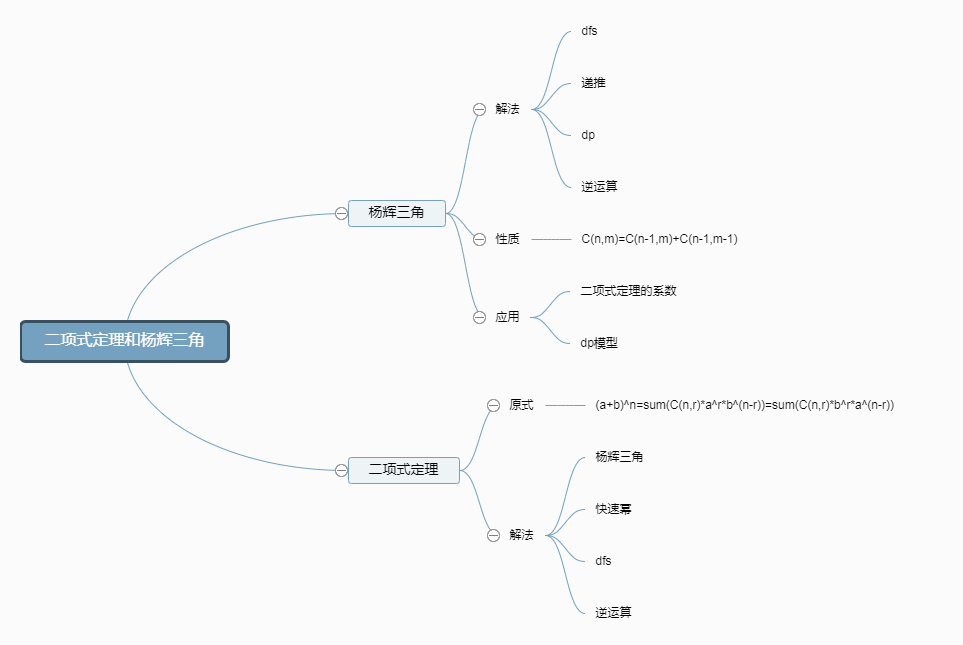
杨辉三角

解法1：dfs

使用记忆化搜索，提升dfs效率

代码：

int dfs(int n,int m){
	if(!m)return c[n][m]=1;
	if(m==1)return c[n][m]=n;
	if(c[n][m])return c[n][m];
	if(n-m<m)m=n-m;
	return c[n][m]=(dfs(n-1,m)+dfs(n-1,m-1))%mod;
}

解法2：递推

时间复杂度O(n^2)，如果n较大，建议使用逆运算的方法

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e4+39+7;
ll a[N][N],n,m;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)a[i][1]=a[i][i]=1;
	for(int i=2;i<=n;i++){
		for(int j=2;j<=n;j++){
			a[i][j]=a[i-1][j]+a[i-1][j-1];
		}
	}
	cout<<a[n][m];
	return 0;
}

解法3：逆运算

速度最快，但是涉及到阶乘，所以需要取模

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e3+1,mod = 1e4+7;
short int fac[N],inv[N];
int quickPow(int a,int n){
	int ans=1;
	a%=mod;
	while(n){
		if(n&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		n>>=1;
	}
	return ans;
}
int c(int n,int m){
	return (fac[n]*inv[m]%mod*inv[n-m]%mod)%mod;
}
int main(){
	int a,b,n,m,k;cin>>a>>b>>k>>n>>m;
	fac[0]=1;
	for(int i=1;i<=n+m;i++){
		fac[i]=(fac[i-1]*i)%mod;
		inv[i]=quickPow(fac[i],mod-2);
	}
	cout<<(quickPow(a,n)%mod*quickPow(b,m)%mod*c(k,n)%mod);
	return 0;
}

杨辉三角使用了组合数的第2个性质：C(n,r)=C(n-1,r)+C(n-1,r-1)

杨辉三角的主要应用是二项式定理与dp基础模型

二项式定理

二项式定理原式：(a+b)ⁿ=sum(C(n,r)*a^r*b^n-r)=sum(C(n,r)*b^r*a^n-r)

下面给出一道例题：P1313 [NOIP2011 提高组] 计算系数

根据二项式定理，直接求得答案

解法1：dfs

又慢又耗空间

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e3+39+7,mod = 1e4+7;
int c[N][N];
int quickPow(int a,int n){
	int ans=1;
	a%=mod;
	while(n){
		if(n&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		n>>=1;
	}
	return ans;
}
int dfs(int n,int m){
	if(!m)return c[n][m]=1;
	if(m==1)return c[n][m]=n;
	if(c[n][m])return c[n][m];
	if(n-m<m)m=n-m;
	return c[n][m]=(dfs(n-1,m)+dfs(n-1,m-1))%mod;
}
int main(){
	int a,b,k,n,m;cin>>a>>b>>k>>n>>m;
	c[1][0]=c[1][1]=1;
	int ans=1;
	ans*=(quickPow(a,n)*quickPow(b,m))%mod;
	ans*=dfs(k,n)%mod;
	cout<<ans%mod;
	return 0;
}

解法2：逆运算

最快且最省空间

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e3+39+7,mod = 1e4+7;
int fac[N],inv[N];
int quickPow(int a,int n){
	int ans=1;
	a%=mod;
	while(n){
		if(n&1)ans=(ans*a)%mod;
		a=(a*a)%mod;
		n>>=1;
	}
	return ans;
}
int c(int n,int m){
	return (fac[n]*inv[m]%mod*inv[n-m]%mod)%mod;
}
int main(){
	int a,b,n,m,k;cin>>a>>b>>k>>n>>m;
	fac[0]=1;
	for(int i=1;i<=n+m;i++){
		fac[i]=(fac[i-1]*i)%mod;
		inv[i]=quickPow(fac[i],mod-2);
	}
	cout<<(quickPow(a,n)%mod*quickPow(b,m)%mod*c(k,n)%mod);
	return 0;
}

二项式定理二项式定理arrangement