微积分

一、函数与极限

极限是啥？极限就是你可以无限逼近你的女神，但是你永远追不到；极限就是你可以无限逼近死亡，但是你妈妈打你绝对不会把你打死；极限就是你可以天天奖励直至巅峰，但是你一定到不了极乐世界。

开个玩笑。那么极限到底是啥呢？请听我细细说来。

1.1数列的极限

数列，就是一排数搁这儿依次排队排好了。第一个记为 $x_1$ ，第二个记为 $x_2$ ，以此类推一直到 $x_n$ ，也有可能一直排下去无穷无尽。我们把整个队列加个大括号记作 $\{x_n\}$。如果这个队列有一定规律，我就可以得到它的通式，比如说 $x_n=n^2$ 或者 $x_n=n$ 。

这一节其实你可以不用看，我一句话给你说完：数列的极限就是说，如果这个很长很长的数的队列有极限，那就意味着到最后的那些数都趋向于相同了。

对于数列 $\{x_n\}$ ，如果当 $n$ 无限增大时， $x_n$ 无限趋近一个常数 $A$ ，则称当 $n$ 趋于无穷时，数列 $\{x_n\}$ 以 $A$ 为极限，记作：

\[\lim\limits_{n\to\infty}{x_n}=A\\ \]

这个式子叫（翻译成中文就是）：当$n$ 趋于无穷时，数列 $\{x_n\}$ 的极限是 $A$ 。

【例1】求下列数列的极限。

（1）$x_n=\frac{1}{n}$

（2）$x_n=1+\frac{1}{2^n}$

（3）$x_n=n^2$

【分析】

（1）$\lim\limits_{n\to\infty}{x_n}=\lim\limits_{n\to\infty}{\frac{1}{n}}=0$

（2）$\lim\limits_{n\to\infty}{x_n}=\lim\limits_{n\to\infty}{(1+\frac{1}{2^n})}=1$

（3）$\lim\limits_{n\to\infty}{x_n}=\lim\limits_{n\to\infty}{n^2}=\infty$

1.2函数的极限

（1）自变量趋于无穷大时函数的极限

如果 $|x|$ 无限增大时， $f(x)$ 无限接近于 $A$ ，则称 $A$ 为函数 $f(x)$ 当 $x\to\infty$ 时的极限，记作：

$\lim\limits_{x\to\infty}{f(x)}=A\\$ 注： $\lim\limits_{x\to\infty}{f(x)}=A$ 需要保证 $\lim\limits_{x\to+\infty}{f(x)}=A$ 且 $\lim\limits_{x\to-\infty}{f(x)}=A$ ，其实就是说当 $x$ 很小或者很大的时候 $f(x)$ 都要趋于 $A$ 才可以。

【例2】分析下列函数在 $x\to\infty$ 时的极限。

① $f(x)=2^x$

② $f(x)=2^{-x}$

③ $f(x)=2^{-x^2}$

【解析】

① $\lim\limits_{x\to+\infty}2^x=\infty,\lim\limits_{x\to-\infty}2^x=0,$ 因此 $f(x)$ 在 $x\to\infty$ 时没有极限。

② $\lim\limits_{x\to+\infty}2^{-x}=0,\lim\limits_{x\to-\infty}2^{-x}=\infty,$ 因此 $f(x)$ 在 $x\to\infty$ 时没有极限。

③ $\lim\limits_{x\to+\infty}2^{-x^2}=0,\lim\limits_{x\to-\infty}2^{-x^2}=0,$ 因此极限 $\lim\limits_{x\to\infty}{f(x)}=0$ 。

（2）自变量趋于有限值时函数的极限

如果 $x$ 无限趋近 $x_0$ ，但 $x\neq x_0$ 时， $f(x)$ 无限接近于 $A$ ，则称 $A$ 为函数 $f(x)$ 当 $x\to x_0$ 时的极限，记作

\[\lim\limits_{x\to x_0}{f(x)}=A\\ \]

此外自变量趋于有限值时函数的极限，还包括从左边靠近和从右边靠近。如果 $x$ 从左边无限趋近 $x_0$ ，但 $x\neq x_0$ 时，有 $f(x)$ 无限接近于 $A$ ，则称 $A$ 为函数 $f(x)$ 当 $x\to x_0$ 时的左极限，记作

\[\lim\limits_{x\to x_0^-}{f(x)}=A\\ \]

同理，如果 $x$ 从右边无限趋近 $x_0$ ，但 $x\neq x_0$ 时，有 $f(x)$ 无限接近于 $A$ ，则称 $A$ 为函数 $f(x)$ 当 $x\to x_0$ 时的右极限，记作

\[\lim\limits_{x\to x_0^+}{f(x)}=A\\ \]

注：

如果极限 $\lim\limits_{x\to x_0}{f(x)}=A$ 存在，则需要保证极限 $\lim\limits_{x\to x_0^+}{f(x)}=A$ 和极限 $\lim\limits_{x\to x_0^-}{f(x)}=A$ 同时存在且相等，也就是说当 $x\to x_0$， $\lim\limits_{x\to x_0^-}{f(x)}=\lim\limits_{x\to x_0^+}{f(x)}=A$ 才能证明$\lim\limits_{x\to x_0}{f(x)}=A$ 存在。

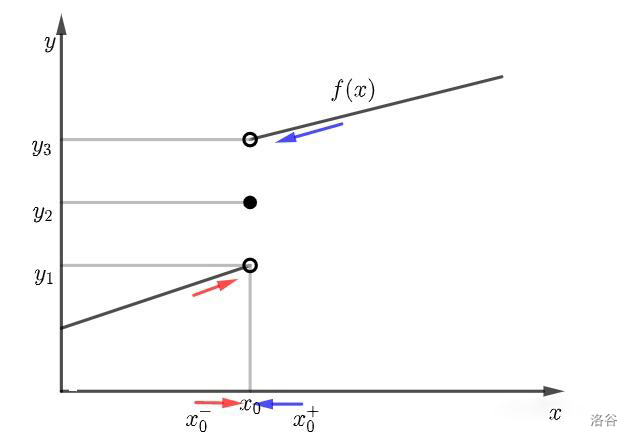
在上图中，左极限就是当 $x$ 从左边趋向于 $x_0$ 时（红色），则极限 $\lim\limits_{x\to x_0^-}f(x)=y_1$ 。
右极限就是当 $x$ 从右边趋向于 $x_0$ 时（蓝色），则极限 $\lim\limits_{x\to x_0^+}f(x)=y_3$ 。
由于在这里 $\lim\limits_{x\to x_0^-}f(x)\ne\lim\limits_{x\to x_0^+}f(x)$ ，因此极限 $\lim\limits_{x\to x_0}f(x)$ 不存在。

【例3】分析下列函数在$x\to x_0$时的极限。

① $f(x)=2^x,x_0=0$

② $f(x)=\frac{1}{x},x_0=0$

【解析】

① $\lim\limits_{x\to 0}{2^x}=1$

② $\lim\limits_{x\to 0}{\frac{1}{x}}=\infty$ ，函数无极限。

【例4】分析函数 $f(x)=2^x$ 在 $x_0=0$ 处的左右极限和极限。（注意一下左右极限和极限的区别）

【解析】

① 左极限： $\lim\limits_{x\to 0^-}{2^x}=1$

② 右极限： $\lim\limits_{x\to 0^+}{2^x}=1$

③ 极限： $\lim\limits_{x\to 0}{2^x}=1$

1.3函数的连续

函数在某一点连续，就代表函数在这一点的左极限等于右极限并且函数在该点的值也要等于左右极限。（这很显然，但是很基础，就像你不知道1+1=2可能会当场去世一样）

用数学语言描述：

\[\lim\limits_{x\to x_0^-}{f(x)}=\lim\limits_{x\to x_0^+}{f(x)}=f(x_0)\\ \]

或者写成

\[\lim\limits_{x\to x_0}{f(x)}=f(x_0)\\ \]

1.4无穷小和无穷大

（1）无穷小的定义：说白了就是一个很小的东西，但还不至于和0一样小。

\[\lim\limits_{x\to a}f(x)=0\\ \]

很常用的有：当 $x\to 0$ 时， $x,x^2,x^3,\sqrt{x}$ 都是无穷小。

（2）无穷大的定义：说白了就是一个很大的东西，大到你不知道它有多大。一般都是把无穷小倒数一下。但是由于趋向于0有两个方向，所以也有正无穷和负无穷。但是说实话，学物理的不喜欢无穷大的东西，所以一般我们都是处理它的倒数，也就是我们一般把无穷大倒数一下当作无穷小去处理。

（3）无穷小的性质

① 有限个无穷小的和还是无穷小。
② 有界函数与无穷小的乘积是无穷小。

（4）无穷小的比较

两个无穷小的差别是什么？差别就是趋向于0的速度不同，有些要快，有些要慢。举个例子：当 $x\to 0$ 时， $x^3$ 显然比 $x^2$ 趋向于0的速度更快，那么我们怎么判断两个无穷小的大小呢？请看下方。

① 除法判断法

如果 $\lim{\frac{\beta}{\alpha}}=0$ ，则称 $\beta$ 是$\alpha$ 的高阶无穷小，记作 $\beta=o(\alpha)$ 。

如果$\lim{\frac{\beta}{\alpha}}=C$ ，则称 $\beta$ 是$\alpha$ 的同阶无穷小。特别的当$\lim{\frac{\beta}{\alpha}}=1$ ，则称 $\beta$ 是$\alpha$ 的等价无穷小，记作 $\alpha\sim\beta$ 。

② k阶无穷小

如果$\lim{\frac{\beta}{\alpha^k}}=C(C\neq 0,k>0)$ ，则称 $\beta$ 是$\alpha$ 的k阶无穷小。举个例子，当 $x\to 0$ 时， $x^4$ 是 $x^2$ 的2阶无穷小。

如果在一个式子里同时有两项无穷小，另一个是高阶无穷小，那我们就可以把高阶无穷小给舍去。

1.5等价无穷小

等价无穷小有很多例子，有些是非常神奇和非常漂亮的例子。常用的有如下几个，大家务必记住，之后会用到。

\[\sin{x}\sim x\\ \tan{x}\sim x\\ \ln(1+x)\sim x\\ e^x\sim x+1\\ \cos{x}\sim1-\frac{1}{2}x^2\\ \]

1.6常用极限

我们只有一个常用极限及其变式，大家记住它，因为它是绝美的。

\[\lim\limits_{n\to\infty}{(1+\frac{1}{n})^n}=e\\ \lim\limits_{x\to0}{(1+x)^{\frac{1}{x}}}=e\\ \]

上面两个极限是没有道理的，因为这是一个发现，人们发现它等于自然常数 $e$ ，这是很奇妙的。

二、导数与微分

2.1一元函数微分和导数的定义

（1）一元函数的定义

一元函数就是只有一个自变量的函数，我们可以轻易画出它在直角坐标系中的图像，比较形象。一般用 $y=y(x)$ 或者 $y=f(x)$ 表示。

（2）增量

① 自变量增量 $\Delta x$ ，这是我们的一个人为操作，假设 $x $ 变化 $\Delta x$ ，我们的目的是想知道 $y$ 变化了多少。

② 应变量增量 $\Delta y=y(x+\Delta x)-y(x)$ ，现在我们要解决的问题是 $\Delta y$ 怎么用 $\Delta x$ 表示，大家请看下面几个例题练练手。

【例5】求下面函数的增量（求应变量增量 $\Delta y$ ，假设自变量增量为 $\Delta x$ ）

① $y=Ax+B$

② $y=Ax^2$

③ $y=\sin{x}$

④ $y=e^x$

【解析】

① $\Delta y=y(x+\Delta x)-y(x)=A(\Delta x+x)+B-Ax-B=A\Delta x$

② $\Delta y=A(\Delta x+x)^2-Ax^2=2Ax\Delta x+A(\Delta x)^2$

③ $\Delta y=\sin{(\Delta x+x)}-\sin{x}\\=\sin{\Delta x}\cos{x}+\cos{\Delta x}\sin{x}-\sin{x}$

特别的，当 $\Delta x\to0$ 时，根据我们在第一章里学的极限和等价无穷小，我们可以得到 $\cos{\Delta x}=1$ 和 $\sin{\Delta x}\sim\Delta x$ ，所以有如下结果

$\Delta y=\sin{\Delta x}\cos{x}+\cos{\Delta x}\sin{x}-\sin{x}\\=\Delta x\cos{x}+\sin{x}-\sin{x}\\=\cos{x}\Delta x$

④ $\Delta y=e^{(x+\Delta x)}-e^x=e^x(e^{\Delta x}-1)$

根据之前的等价无穷小，特别的当 $\Delta x\to0$ 时，有 $e^{\Delta x}-1\sim \Delta x$ ，所以有如下结果

$\Delta y=e^x(e^{\Delta x}-1)=e^{x}\Delta x$

（3）微分：

为了体现出微积分的伟大，$\text{d}$叫做微分符号，我们把 $\Delta x\to0$ 时的 $\Delta x$ 写为 $\text{d}x$ ，叫做自变量的微分（其实就是一个很小的量，所以叫“微”；之所以叫“分”现在还不好解释，它有更深的涵义在里面，我们放到后面讲）。那么很显然，我们把 $\Delta y\to0$ 时的 $\Delta y$ 写为 $\text{d}y$ ，叫做应变量的微分。并且有一点很显然，当 $\Delta x\to0$ 时，对应的 $\Delta y\to0$。

注：

① 这个 $\text{d}$ 有些地方是斜体，有些地方是正体，各有各的好处。正体的好处：一眼就能认出来，还能区别于直径的 $d$ ，所以学物理的一般用正体写 $\text{d}$ 。斜体的好处：如果微分符号写得多的话，用斜体比较方便，所以数学家一般用斜体。

② 强调一下微分的目的是什么：微分就是想通过$\text{d}x$的变化，来表示$\text{d}y$的变化。所以大家能够理解到我把函数增量放在微分之前的用意了吗？就是想让你通过类比，认识到微分不过是增量的极限。

（4）导数（微商）：

导数就是微商。微商就是两个微分之商。

\[\frac{\text{d}y}{\text{d}x}=\lim\limits_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\lim\limits_{\Delta x\to0}\frac{y(x+\Delta x)-y(x)}{\Delta x}\\ \]

大家用函数增量把 $y(x+\Delta x)-y(x)$ 代掉，会发现一件神奇的事情： $\Delta x$ 被约掉了。

① 导数的表示方法： $y^{\prime}\\$

② 微商的表示方法：

\[\frac{\text{d}y}{\text{d}x}=\frac{\text{d}f(x)}{\text{d}x}=\frac{\text{d}f}{\text{d}x}\\ \]

两种表示方法可以互通。

2.2导数的几何意义

（1）导数的几何意义

大家直接看图，这是一个普通的函数，从图中可以看出：当自变量 $x$ 变化 $\text{d}x$ 时，应变量 $y$ 变化 $\text{d}y$ 。那么现在大家来思考一下， $\frac{\text{d}y}{\text{d}x}$ 代表什么意思呢？ $\frac{\text{d}y}{\text{d}x}$就表示直线 $l_{AB}$ 的斜率。

现在我们假设$\text{d}x$不断变小，那么 $\text{d}y$ 也不断变小，换句话说，点 $B$ 不断向着点 $A$ 靠近，那么我们就得到了两个靠的很近的点的直线斜率，也就是点 $A$ 处的切线斜率。

结论：导数的几何意义，就是某一点的切线斜率。

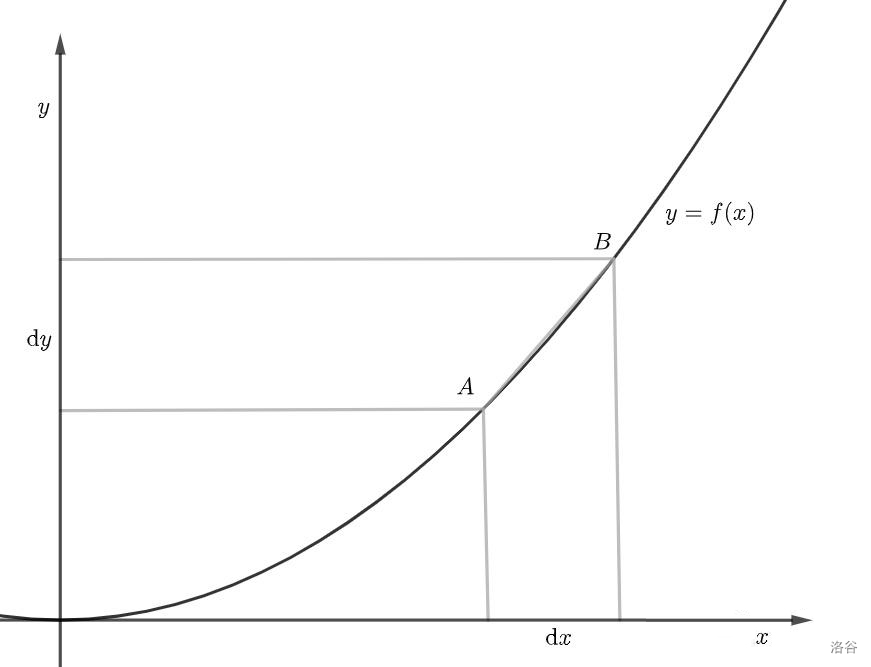
直线的斜率就是应变量变化量除以自变量变化量。

（2）切线的表示方法

我们既然现在知道刚刚我们的操作求出了 $A$ 点的斜率，那么如何表示呢？我们可以表示成：

\[y^\prime\bigg|_{x=x_A}=\frac{\text{d}y}{\text{d}x}\bigg|_{x=x_A}\\ \]

只不过是加一个竖线，并且标上点的横坐标就可以了，这有手就行。

2.3基本函数的导数

对于一般基本函数的导数，其实先人都给大家算好了，大家自己推导一遍然后背出来就完事了，不用纠结太多。

（1）一次函数的导数

\[y=Ax+B,y^\prime=\frac{\text{d}y}{\text{d}x}=A\\ \]

（2）二次函数的导数

\[y=Ax^2+Bx+C,y^\prime=\frac{\text{d}y}{\text{d}x}=2Ax+B\\ \]

（3）正弦函数的导数

\[y=\sin{x},y^\prime=\frac{\text{d}y}{\text{d}x}=\cos{x}\\ \]

（4）自然指数函数的导数（我导完竟是我自己！？）

\[y=e^x,y^\prime=\frac{\text{d}y}{\text{d}x}=e^x\\ \]

【证明】

（1）一次函数的导数

应变量增量：

\[\Delta y=y(x+\Delta x)-y(x)=A(\Delta x+x)+B-Ax-B=A\Delta x\\ \therefore y^\prime=\frac{\text{d}y}{\text{d}x}=\lim\limits_{\Delta x\to0}\frac{\Delta y}{\Delta x}=A\\ \]

（2）二次函数的导数

应变量增量：

\[\Delta y=A(x+\Delta x)^2+B(x+\Delta x)+C-Ax^2-Bx-C=(2Ax+B)\Delta x+A(\Delta x)^2 \]

由于对于 $\Delta x$ ， $(\Delta x)^2$ 是二阶小量，所以我们可以把它舍去。（大家忘了的话可以查看1.4节），现在我们就得到了 $\Delta y$ 的最终表达式

\[\Delta y=(2Ax+B)\Delta x \\ \therefore y^\prime=\frac{\text{d}y}{\text{d}x}=\lim\limits_{\Delta x\to0}\frac{\Delta y}{\Delta x}=2Ax+B\\ \]

（3）正弦函数的导数

应变量增量：

\[\Delta y=\sin{(\Delta x+x)}-\sin{x}=\sin{\Delta x}\cos{x}+\cos{\Delta x}\sin{x}-\sin{x} \]

当 $\Delta x\to0$ 时，根据之前讲的极限和等价无穷小（1.4节），我们可以得到 $\cos{\Delta x}=1$ 和 $\sin{\Delta x}\sim\Delta x$，所以有如下结果

\[\Delta y=\sin{\Delta x}\cos{x}+\cos{\Delta x}\sin{x}-\sin{x}\\ =\Delta x\cos{x}+\sin{x}-\sin{x}\\=\cos{x}\Delta x\\ \]

现在我们就得到了 $\Delta y$ 的最终表达式：

\[\Delta y=\cos{x}\Delta x\\ \therefore y^\prime=\frac{\text{d}y}{\text{d}x}=\lim\limits_{\Delta x\to0}\frac{\Delta y}{\Delta x}=\cos{x}\\\]

（4）自然指数函数的导数（我导完竟是我自己！？）

应变量增量：

\[\Delta y=e^{(x+\Delta x)}-e^x=e^x(e^{\Delta x}-1) \]

根据之前的等价无穷小，特别的当 $\Delta x\to0$ 时，有 $e^{\Delta x}-1\sim \Delta x$ ，所以得到了 $\Delta y$ 的最终表达式

\[\Delta y=e^x(e^{\Delta x}-1)=e^{x}\Delta x\\ \therefore y^\prime=\frac{\text{d}y}{\text{d}x}=\lim\limits_{\Delta x\to0}\frac{\Delta y}{\Delta x}=e^x\\ \]

2.4导数的运算法则

（1）基本的函数求导法则

函数的求导法则主要有四个：加法法则、乘法法则、除法法则、链式法则（又名复合函数求导法则）

① 加法法则：若 $y=Ay_1+By_2$ ，

则 $y^\prime=Ay^\prime_1+By^\prime_2$

$\Delta y=y(x+\Delta x)-y(x)\\ =Ay_1(x+\Delta x)+By_2(x+\Delta x)-Ay_1(x)-By_2(x)\\ =(Ay_1(x+\Delta x)-Ay_1(x))+(By_2(x+\Delta x)-By_2(x))\\ =A\Delta y_1+B\Delta y_2$

因此 $y^\prime=\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}\\ =\lim\limits_{\Delta x\to 0}\frac{A\Delta y_1+B\Delta y_2}{\Delta x}\\ =\lim\limits_{\Delta x\to 0}\frac{A\Delta y_1}{\Delta x}+\lim\limits_{\Delta x\to 0}\frac{B\Delta y_2}{\Delta x}\\ =Ay_1^\prime+By_2^\prime$

② 乘法法则：若 $y=y_1y_2$ ，

则 $y^\prime=y^\prime_1y_2+y_1y^\prime_2$ （前导后不导加前不导后导）

$\Delta y=y(x+\Delta x)-y(x)=y_1(x+\Delta x)\cdot y_2(x+\Delta x)-y_1\cdot y_2\\ =y_1(x+\Delta x)\cdot y_2(x+\Delta x)-y_1(x)\cdot y_2(x+\Delta x)\\+y_1(x)\cdot y_2(x+\Delta x)-y_1(x)\cdot y_2(x)\\ =\left[y_1(x+\Delta x)-y_1(x)\right]y_2(x+\Delta x) + \left[y_2(x+\Delta x) - y_2(x)\right]y_1(x) \\=\Delta y_1\cdot y_2(x+\Delta x)+\Delta y_2\cdot y_1(x)\\ =\Delta y_1\cdot y_2(x)+\Delta y_2\cdot y_1(x)$

因此 $y^\prime=\lim\limits_{\Delta x\to 0}\frac{\Delta y}{\Delta x}\\ =\lim\limits_{\Delta x\to 0}\frac{\Delta y_1\cdot y_2(x+\Delta x)+\Delta y_2\cdot y_1(x)}{\Delta x}\\ =\lim\limits_{\Delta x\to 0}\frac{\Delta y_1\cdot y_2(x+\Delta x)}{\Delta x}+\lim\limits_{\Delta x\to 0}\frac{\Delta y_2\cdot y_1(x)}{\Delta x}\\ =y_1^\prime y_2+y_1y_2^\prime$

③ 除法法则：若 $y=\frac{y_1}{y_2}$ ，

则 $y^\prime=\frac{y^\prime_1y_2-y_1y^\prime_2}{y_2^2}$ ，（前导后不导减前不导后导，除以后不导的平方）

将原式写成 $y = y_1\cdot\frac{1}{y_2}$ ，然后根据乘法法则可以得到（不过这里的第二步也用到了链式法则）

\[\begin{align} y &= y_1^\prime\cdot \frac{1}{y_2} + y_1\cdot \left(\frac{1}{y_2}\right)^\prime\\ &=y_1^\prime\cdot \frac{1}{y_2} + y_1\cdot \left(\frac{-y_2^\prime}{y_2^2}\right)\\ &=\frac{y_1^\prime y_2 - y_1y_2^\prime}{y_2^2} \end{align}\\ \]

④ 链式法则：若 $y=y[u(x)]$ ，

则 $y^\prime=\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}\cdot\frac{\text{d}u}{\text{d}x}=y^\prime[u(x)]u^\prime(x)$

\[\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}\cdot\frac{\text{d}u}{\text{d}x} \]

这是链式法则的精髓：在其中乘上 $\text{d}u$ 又除以 $\text{d}u$ ，一个导数就变成两个导数了，然后分别计算就可以了。

（2）高级求导法则

① 隐函数求导法则

隐函数是指由方程确定的函数，但是我们很难求出它的显式。例如 $\sin{y}+e^y=x^2$ 可以是一个函数，但是我们求不出来具体的 $y=f(x)$ 。对隐函数求导的求解过程就是方程两边同时对 $x$ 求导，然后解 $y^\prime$ 。

【例6】求 $e^y-x^2y+e^x=0$ 所确定函数的导数。

【解析】两边同时对 $x$ 求导，得到

\[\frac{\text{d}e^y}{\text{d}x}-\frac{\text{d}x^2y}{\text{d}x}+\frac{\text{d}e^x}{\text{d}x}=0\\ \frac{\text{d}e^y}{\text{d}y}\frac{\text{d}y}{\text{d}x}-\frac{\text{d}x^2}{\text{d}x}y-x^2\frac{\text{d}y}{\text{d}x}+e^x=0\\ e^y\frac{\text{d}y}{\text{d}x}-2xy-x^2\frac{\text{d}y}{\text{d}x}+e^x=0\\ \]

然后解 $y^\prime$

\[\therefore y^\prime=\frac{\text{d}y}{\text{d}x}=\frac{2xy-e^x}{e^y-x^2}\\ \]

在这里用到了链式法则、乘法法则、加法法则，大家可以品味一下。

② 参数方程求导法则

参数方程就是多引入了一个变量，同时表示 $x,y$ 。例如 $x=2t,y=4t$ ，那么显然就能得到函数 $y=f(x)=2x$ 。但是更一般的，我们有：

$x=\varphi(t)\\ y=\psi(t)\\$ 这时候怎么办呢？

\[\frac{\text{d}y}{\text{d}x}=\frac{\frac{\text{d}y}{\text{d}t}}{\frac{\text{d}y}{\text{d}t}}=\frac{x^\prime}{y^\prime}=\frac{\psi^\prime(t)}{\varphi^\prime(t)}\\ \]

我们不过是上下同时除以 $\text{d}x$ ，就把一个对 $x$ 的求导，变成了两个对 $t$ 的求导。

【例7】已知由参数方程确定的函数$\begin{cases}y=\varphi-R\sin{\varphi}\\x=\cos{\varphi}\\\end{cases}$ ，求函数的导数。

【解析】

\[\frac{\text{d}y}{\text{d}x}=\frac{\frac{\text{d}y}{\text{d}\varphi}}{\frac{\text{d}y}{\text{d}\varphi}}=\frac{1-R\cos{\varphi}}{-\sin{\varphi}}\\ \]

（3）常见函数的求导公式

\[(C)^\prime=0\\ (x^a)^\prime=ax^{a-1}\\ (\sin{x})^\prime=\cos{x}\\ (\cos{x})^\prime=-\sin{x}\\ (\tan{x})^\prime=\sec^2{x}\\ (\cot{x})^\prime=-\csc^2{x}\\ (\sec{x})^\prime=\sec{x}\tan{x}\\ (\csc{x})^\prime=-\csc{x}\cot{x}\\ (a^x)^\prime=a^x\ln{a}\\ (e^x)^\prime=e^x\\ (\log_a{x})^\prime=\frac{1}{x\ln{a}}\\ (\ln{x})^\prime=\frac{1}{x}\\ (\arcsin{x})^\prime=\frac{1}{\sqrt{1-x^2}}\\ (\arccos{x})^\prime=-\frac{1}{\sqrt{1-x^2}}\\ (\arctan{x})^\prime=\frac{1}{1+x^2}\\ (\text{arccot}{x})^\prime=-\frac{1}{1+x^2} \]

2.5高阶导数

（1）高阶导数是求完一次导还不够，要求第二次，甚至第三次，一直往下求。因为每次求完导以后我们得到的还是 $x$ 的函数 $y^\prime$ ，所以理论上还可以再求导。

（2）表示方法

求导两次

\[y^{\prime\prime}=\frac{\text{d}^2y}{\text{d}x^2}\\ \]

求导三次

\[y^{\prime\prime\prime}=\frac{\text{d}^3y}{\text{d}x^3}\\ \]

求导 $n$ 次

\[y^{(n)}=\frac{\text{d}^ny}{\text{d}x^n}\\ \]

2.6导数和函数的关系

（1）单调性

① $y^\prime>0$ ，函数的切线就斜向右上，所以函数单调递增。
② $y^\prime<0$ ，函数的切线就斜向右下，所以函数单调递减。

在A左边导数为正，函数单增。A和B的中间导数为负，函数单减。B的右边导数为正，函数单增。

（2）极大值和极小值

① $y^\prime=0,$ $y^{\prime\prime}>0$ ，函数的一阶导数单增，所以函数的一阶导数在左边为负值，右边为正值；函数先单减，导数变为0后再单增；函数开口向上，为极小值。
② $y^\prime=0,$ $y^{\prime\prime}<0$ ，函数的一阶导数单减，所以函数的一阶导数在左边为正值，右边为负值；函数先单增，导数变为0后再单减；函数开口向下，为极大值。

如图中 $A$ 点就是极大值， $B$ 点就是极小值。但 $A,B$ 显然不是区间内的最大值或者最小值。因此极大值和极小值只是函数局部的性质。

2.7泰勒公式

又到了一天一度的装13环节，大家学会了这个就可以在同学面前装13了，咳咳咳。

（1）概念引入

如果我们知道 $y=f(x_0)$ 处的值，现在我们想知道 $y=f(x_0+\Delta x)$ 处的值，我们怎么办呢？（有同学问，你不是都写出来了，还问我们干嘛？）

其实现在的问题是， $f(x)$ 可能是一个十分复杂的函数，难以用初等函数来表示，我们能不能找到一个公式，用 $\Delta x$ 的多项式来表示 $f(x+\Delta x)$ 呢？泰勒给出了答案。

（2）具体内容

泰勒公式：

\[y\bigg|_{x=x_0+\Delta x}=f(x_0+\Delta x)=f(x_0)+\sum\limits_{n=1}\limits^{\infty}{}\frac{1}{n!}\frac{\text{d}^ny}{\text{d}x^n}\bigg|_{x_0}(\Delta x)^n\\ \]

写得简单一点

\[f(x_0+\Delta x)=f(x_0)+\frac{1}{1!}f^\prime(x_0)\Delta x+\frac{1}{2!}f^{\prime\prime}(x_0)(\Delta x)^2+\frac{1}{3!}f^{\prime\prime\prime}(x_0)(\Delta x)^3+...\\ \]

别看它很长，但是其实它只要算 $\Delta x$ 的次方就好了，对于计算机来说这是一件方便的事情。

（3）用泰勒公式计算无穷小量的等价

可以回顾一下（1.5节等价无穷小），接下来我将给出几个常用等价无穷小的计算。计算的时候只取泰勒公式的前三项，并且令 $x_0=0$ 。

\[f(0+\Delta x)=f(0)+f^\prime(0)\Delta x+\frac{1}{2}f^{\prime\prime}(0)(\Delta x)^2\\ \]

① $\sin{x}\sim x(x\to0)$

\[f(0+x)=\sin{0}+\cos{0} \cdot x-\sin{0}\cdot(x)^2=x\\ \]

② $\cos{x}\sim 1-\frac{x^2}{2}(x\to0)$

\[f(x)=\cos{0}-\sin{0} \cdot x-\cos{0}\cdot(x)^2=1-\frac{x^2}{2}\\ \]

③ $\tan{x}\sim x (x\to0)$

\[f(x)=\tan{0}+\frac{1}{\cos^2{0}}\cdot x+\frac{\sin{0}}{\cos^3{0}}\cdot(x)^2=x\\ \]

④ $e^x\sim x+1(x\to0)$

\[f(x)=e^0+e^0\cdot x+\frac{1}{2}e^0\cdot(x)^2=1+x+\frac{x^2}{2}\\ \]

一般到不了二阶无穷小量的精度，所以把 $\frac{x^2}{2}$ 舍去就好了。

⑤ $\ln(x+1)\sim x(x\to 0)$

\[f(x)=\ln{1}+\frac{1}{1+0}\cdot x-\frac{1}{2}\frac{1}{(1+0)^2}\cdot(x)^2=x-\frac{x^2}{2}\\ \]

一般到不了二阶无穷小量的精度，所以也把 $\frac{x^2}{2}$ 舍去就好了。

2.8洛必达法则

说实话呢，这个还是装13环节，咳咳咳。

（1）概念

洛必达法则是用来求特殊情况下的极限的。哪些特殊情况呢？分子和分母都是无穷小量的情况 $\frac{0}{0}$ 型和分子和分母都是无穷大的情况 $\frac{\infty}{\infty}$ 。由于无穷大倒数一下就是无穷小，所以我们一般只会用到无穷小量的洛必达。

（2）具体表述

若函数 $f(x),g(x)$ 满足：
① $\lim\limits_{x\to a}f(x)=0,\lim\limits_{x\to a}f(x)=0;$ （就是分子和分母都是无穷小量）
② $f(x),g(x)$ 可导，且 $g^\prime(x)\neq 0;$
③ $\lim\limits_{x\to a}\frac{f^\prime(x)}{g^\prime(x)}=A;$
则

\[\lim\limits_{x\to a}\frac{f(x)}{g(x)}=\lim\limits_{x\to a}\frac{f^\prime(x)}{g^\prime(x)}=A\\ \]

其实洛必达法则讲的是，求极限上下都是无穷小怎么办？上下求导看一看。

2.9曲率和曲率半径

这东西还是给你装13的，这是物竞党的骄傲，毕竟曲率和曲率半径说出去多厉害啊。这一节我们要解决的问题是，我们已知一条曲线的方程 $y=f(x)$ ，怎么求它各处的曲率半径。

（1）曲率

曲率 $K$ 是用来描述曲线上某点的弯曲程度的物理量， $K=\frac{1}{\rho}$ ，其中 $\rho$ 是一个曲线的曲率半径。

（2）曲率半径

如果我们把一条曲线上的一小段看成是一个圆弧，那么我们必然能把这个圆弧对应的圆给画出来，并且把圆的圆心和半径求出来。而这个半径就叫做曲率半径，记为 $\rho$ 。

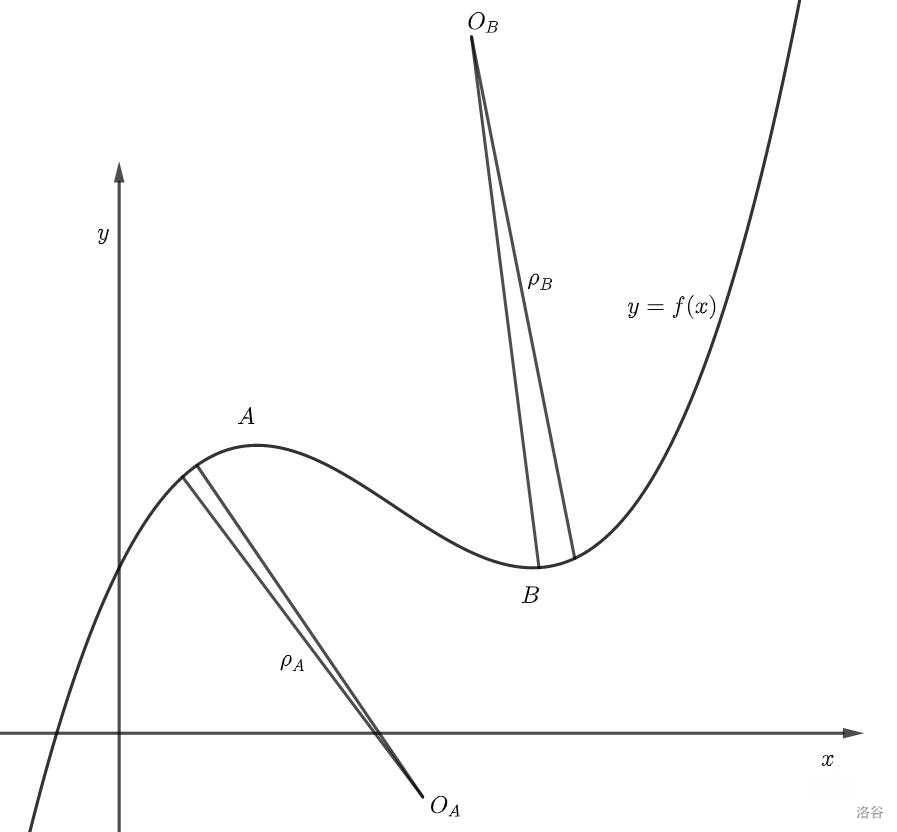
这里我选了一个靠近A点的弧，和另一个靠近B点的弧。

曲率半径公式如下：

\[\rho=\frac{1}{K}=\frac{(1+y^{\prime2})^\frac{3}{2}}{|y^{\prime\prime}|}\\ \]

三、不定积分

昨天刚讲过微分和导数，你回想一下，微分和导数说到底是一种对函数的运算（这该死的欲望，人类已经不满足于把玩数字了，现在要把玩函数了）。经过上一篇文章的学习，现在你可以操作一个函数，把它求导、求微商变成另一个函数，那么你能不能把它变回来呢？所以，这时候就要谈到积分的概念了。

3.1不定积分的概念

（1）概念

不定积分，就是导数的逆运算。你可以什么都不知道，但是不能不知道前面这句话。就像你可以没心没肺，但你始终忘不了ta。

\[y=f(x)\Longleftrightarrow y^\prime=f^\prime(x)\\ \]

上面的式子，从左到右就是求导（微分），从右到左就是积分。这是很自然的一件事情，就像你是你妈的孩子，你妈是你的妈。

（2）特点

虽然说不定积分是导数的逆运算，但是我们在算不定积分的时候会缺失一部分信息。直观地说，因为求导会使得函数失去绝对位置的信息，只保留相对位置的信息。就像时间可以顺着走，但是我们没办法逆转时间一样。

举个例子， $x^2+1$ 和 $x^2+2$ 求完导都是 $2x$ ，因此我们失去了原函数的常数信息，只留下了原函数每一点切线的斜率信息。所以， $2x$的积分既包括 $x^2+1$ ，也包括 $x^2+2$ ，那么我们可以想见 $2x$ 的不定积分就是 $x^2+C$ ， $C$ 是一个常数。这就是不定积分的由来。

3.2不定积分运算方法

（1）常见函数的不定积分

\[\int{k\text{d}x}= +C\\ \int{x^\mu\text{d}x}=\frac{x^{\mu+1}}{\mu+1}+C\\ \int{\frac{\text{d}x}{x}}=\ln{|x|}+C\\ \int{\frac{\text{d}x}{1+x^2}}=\arctan{x}+C\\ \int{\frac{\text{d}x}{\sqrt{1-x^2}}}=\arcsin{x}+C\\ \int{\cos{x}}=\sin{x}+C\\ \int{\sin{x}}=-\cos{x}+C\\ \int{\frac{\text{d}x}{\cos^2{x}}}=\int{\sec^2{x}\text{d}x}=\tan{x}+C\\ \int{\frac{\text{d}x}{\sin^2{x}}}=\int{\csc^2{x}\text{d}x}=-\cot{x}+C\\ \int{\sec{x}\tan{x}\text{d}x}=\sec{x}+C\\ \int{\csc{x}\cot{x}\text{d}x}=-\csc{x}+C\\ \int{e^x}=e^x+C\\ \int{a^x}=\frac{a^x}{\ln{a}}+C\\ \]

（2）第一积分换元法

通过变量代换 $u=\varphi(x)$ ，可以得到 $\frac{\text{d}u}{\text{d}x}=\varphi^\prime(x)$ ，把 $\text{d}x$ 乘过去，进而有

$\text{d}u=\varphi^\prime(x)\text{d}x\\$ 最终将形如

$\int f[\varphi(x)]\cdot\varphi^\prime(x)\text{d}x\\$ 的不定积分变成

$\int f(u)\text{d}u\\$ 得出原函数 $F(u)$ 后，再把 $u=\varphi(x)$ 代换回来，因此最终答案是

$F\big[\varphi(x)\big]\\$ 注：
①更多的情况下为了方便，我们也不会特意去换一个变量，可以直接把 $\varphi^\prime(x)$ 放到微分符号的里面，把 $\int f[\varphi(x)]\cdot\varphi^\prime(x)\text{d}x$ 变成

$\int f[\varphi(x)]\cdot\text{d}[\varphi(x)]\\$ 美其名曰把 $\varphi^\prime(x)$ “吸收进去”。进而把 $\varphi(x)$ 看成一个整体，直接积分得到结果 $F\big[\varphi(x)\big]$

【例题】求 $\int\frac{e^{3\sqrt{x}}}{\sqrt{x}}\text{d}x$ 。

【解析】由于 $\text{d}\sqrt{x}=\frac{1}{2}\frac{\text{d}x}{\sqrt{x}}$ ，因此

$\int\frac{e^{3\sqrt{x}}}{\sqrt{x}}\text{d}x=\int\frac{2e^{3\sqrt{x}}}{2\sqrt{x}}\text{d}x\\ =2\int e^{3\sqrt{x}}\text{d}(\sqrt{x})\\ =\frac{2}{3}\int e^{3\sqrt{x}}\text{d}(3\sqrt{x})\\ =\frac{2}{3}e^{3\sqrt{x}}+C\\$ （2）第二积分换元法

第二积分换元法正好是第一积分换元法倒过来，直接令 $x=\psi(t)$ ，代入不定积分进行化简

把形如 $\int f(x)\text{d}x\\$ 的不定积分转化为

$\int f[\psi(t)]\cdot\psi^\prime(t)\text{d}t\\$ 最后求出积分后回代。

有些同学可能认为这样变麻烦了，我们来看一个例题。

【例题】求 $\int\sqrt{a^2-x^2}\text{d}x$ $(a>0)$ 。

令 $x=a\sin{t}$ ，取 $t\in[-\frac{\pi}{2},\frac{\pi}{2}]$ ，这样 $x$ 就可以取遍它的定义域 $[-a,a]$ 了，且有 $\text{d}x=a\cos{t}\text{d}t$ ，这是因为 $\frac{\text{d}x}{\text{d}t}=a\cos{t}$ 。

代入 $x$ 和 $\text{d}x$ 可得

$\int\sqrt{a^2-x^2}\text{d}x=\int a\cos{t}\cdot a\cos{t}\text{d}t\\ =\int a^2\cos^2{t}\text{d}t=\int a^2\frac{1+\cos{2t}}{2}\text{d}t\\ =\frac{a^2}{2}\int{1+\cos{2t}}\text{d}t\\ =\frac{a^2}{2}(t+\frac{\sin{2t}}{2})+C\\ =\frac{a^2}{2}t+\frac{a^2}{2}\sin{t}\cos{t}+C\\$ 由于 $x=a\sin{t}$，因此 $t=\arcsin{\frac{x}{a}}$ ， $\cos{t}=\sqrt{1-\sin^2{t}}=\frac{\sqrt{a^2-x^2}}{a}$ ，代入上式可得

$\int\sqrt{a^2-x^2}\text{d}x\\ =\frac{a^2}{2}\arcsin{\frac{x}{a}}+\frac{x}{2}\frac{\sqrt{a^2-x^2}}{a}+C\\$ 这个积分是不是比你想象的要麻烦。。。

（3）分部积分法

大家还记得求导的乘法法则吗？我换一种写法

$\frac{\text{d}[u(x)v(x)]}{\text{d}x}=\frac{\text{d}[u(x)]}{\text{d}x}v(x)+u\frac{\text{d}[v(x)]}{\text{d}x}\\$ 把上面式子的 $\text{d}x$ 约掉，两边再加一个积分符号

$\int\text{d}[u(x)v(x)]=\int v(x)\text{d}[u(x)]+\int u(x)\text{d}[v(x)]\\$ 所以

$u(x)v(x)=\int v(x)\text{d}[u(x)]+\int u(x)\text{d}[v(x)]\\$ 移项

$\int v(x)\text{d}[u(x)]=u(x)v(x)-\int u(x)\text{d}[v(x)]\\$ 这就是分部积分法。分部积分法的目的是把积分变量和积分函数掉个个儿。

【例题】求 $\int e^x\sin{x}\text{d}x$ 。

【解析】采用分部积分法，先把 $e^x$ 吸收进去，运用一次分部积分法

$\int e^x\sin{x}\text{d}x=\int \sin{x}\text{d}(e^x)\\=e^x\sin{x}-\int e^x\text{d}(\sin{x})\\=e^x\sin{x}-\int e^x\cos{x}\text{d}x\\$ 再把 $e^x$ 吸收进去，再进行一次分部积分法

$e^x\sin{x}-\int e^x\cos{x}\text{d}x\\=e^x\sin{x}-\int \cos{x}\text{d}(e^x)\\=e^x\sin{x}-(e^x\cos{x}-\int e^x\text{d}(\cos{x}))\\=e^x\sin{x}-(e^x\cos{x}+\int e^x\sin{x}\text{d}x)\\$ 最终得到

$\int e^x\sin{x}\text{d}x=e^x\sin{x}-e^x\cos{x}-\int e^x\sin{x}\text{d}x\\$

所以

$\int e^x\sin{x}\text{d}x=\frac{\sin{x}-\cos{x}}{2}e^x\\$

还是非常精妙的。

四、定积分

如果说不定积分是导数的逆运算，你可能认为积分的地位低下。其实定积分一个人就撑起了微积分的一片天下，并且不定积分只不过是定积分的垫脚石。让我们来一探究竟。

4.1积分的真正含义

（1）第一个问题

如果我们画一个典型的 $v-t$ 图像，纵坐标为速度 $v$ ，函数曲线为 $v(t)$ ，横坐标换为$t$ ，现在我们想要求出物体在时间 $0$ 到 $t_0$ 的位移，我们怎么操作？其实只要我们把图像分成一条一条的“细长条”，然后每一个细长条按照矩形的面积计算，最后求和就可以得到最终的面积了。

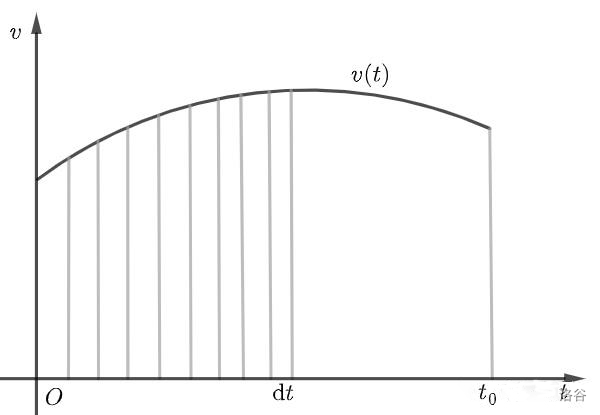
典型的v-t图像

每一个细长条的宽度为 $\text{d}t$ ，长度为 $v(t)$ ，所以一个细长条的面积就是 $v(t)\text{d}t$ ，总的面积就是对 $t$ 从 $0$ 到 $t_0$ 求和，我们用积分代替求和（其实这个积分符号的意思就是求和，然后规定上下限，比用求和符号表示更加简单方便）

如果用求和符号表示，我们需要将总的时间分成 $n$ 份，每份长度为 $\Delta t$ ，同时要让 $n\to\infty$ ，记每次的时间分别记为 $t_1,t_2,t_3,t_4...,t_n$ ，然后求出单个长条的面积 $v(t_i)\Delta t$ ，最终加上极限和求和符号。（我在此处的表达还不够严谨，我已经省去很多繁琐的步骤了，但是大家还是可以看出来这已经很麻烦了）

\[\int_0^{t_0}{v(t)\text{d}t}\Longleftrightarrow\lim\limits_{n\to\infty}\sum\limits_{i=1}\limits^{n}{v(t_i)\Delta t}\\ \]

这个左边的式子就是积分的表达，得出的结果就是总的位移。（大家不太明白不要紧，看我再举另一个例子）

（2）第二个问题

如果我有一个等厚圆盘（半径为 $R$ ，厚度为 $h$ ），它的密度随着半径变化（ $\rho=\rho_0-kr$ ），怎么求它的质量？

从现在开始，积分和微分是一体的了，没有微分，也就没有积分。

（3）问题求解

我现在要介绍的方法又叫微元法（有些低调的大佬不想叫它微积分，但它实际上就是微积分），大家看我操作来解决上面的那个圆盘质量问题。

圆盘的俯视图

这个圆盘的密度是越往外越小的，我在一般的位置（距离圆盘中心距离为 $r$ ）取很小的一段微元 $\text{d}r\to0$ ，那么绕着圆盘一圈的一个窄圆环上的密度是不是近似相等（这就是微元法的核心，取了一个微元以后，我们就可以认为其内部的参数近似相等）。

因为圆环内侧密度是 $\rho(r)$ （此式想表明密度是半径的一个函数），外侧密度是 $\rho(r+\text{d}r)$ ，而 $\text{d}r\to 0$ ，所以密度近似相等。我们取密度为 $\rho(r)$ 。

现在我们就可以求出这个圆环的面积，用大圆的面积减去小圆的面积就可以了。但是这是一个俯视图，所以我们要求的所谓的“面积”实际上是一个薄圆柱壳的体积，同样我可以求出它的体积，进而求出它的质量。说干就干：

\[\text{d}V=h\cdot\text{d}S=h\cdot (\pi(r+\text{d}r)^2-\pi r^2)\\ =h\cdot(2\pi r\text{d}r+\pi(\text{d}r)^2)\\ \]

由于 $\pi(\text{d}r)^2$ 是一个二阶无穷小量，相对于 $2\pi r\text{d}r$ 这个一阶无穷小量可以忽略不计，所以我们把它删去，可以得到

\[\text{d}V=h\cdot2\pi r\text{d}r\\ \]

乘上密度就得到了这一个小小圆柱壳的质量

\[\text{d}m=\rho(r)\text{d}V=\rho(r) h\cdot2\pi r\text{d}r\\=(\rho_0-kr)h\cdot2\pi r\text{d}r\\ \]

为了方便起见，我现在记 $f(r)=(\rho_0-kr)h\cdot2\pi r$，那么

\[\text{d}m=f(r)\text{d}r\\ \]

现在我们来审视一下这个式子，它讲的是什么意思？在距离圆盘距离为 $r$ 处（这个 $r$ 是任意的，既可以是0，也可以非常接近 $R$ ），有一个很薄很薄的厚度为 $\text{d}r$ 的圆柱体壳。我用 $f(r)$ 乘上 $\text{d}r$ ，就可以得到这个薄圆柱壳的质量 $\text{d}m$ 。

最后给它加上积分符号和上下限，代表我们想要求出 $r\in[0,R]$ 内的圆盘质量

\[m=\int_0^R{f(r)\text{d}r}\\ \]

（4）问题转化

我们再进一步，把现在的问题抽象成：已知函数 $f(x)$ ，求它在（ $0<x<R$ ）和 $x$ 轴围成的面积。

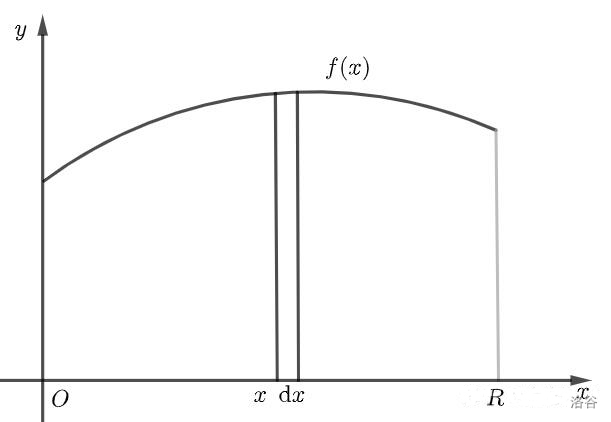
积分它来了，它来了，它来了，它来了，它来了，它来了……

大家看，我在 $x$ 轴上取了一段微元$\text{d}x$ ，那么这一长条的面积就是 $f(x)\text{d}x$ ，因此

\[\text{d}S=f(x)\text{d}x\\ \]

这与 $\text{d}m=f(r)\text{d}r$ 在形式上完全一样，并且 $x$ 和 $r$ 的取值范围都是 $[0,R]$ 。所以只要 $f(x)$ 仍然是原来的那个函数 $f(x)=(\rho_0-kx)h\cdot2\pi x$ ，只不过是换了个自变量而已。 $f(x)$ 保持不变，那么我求出的结果也就不会改变。

所以计算整块总的面积我就给它加上积分符号和上下限：

\[\int_0^{R}{f(x)\text{d}x}\\ \]

上面的例子告诉我们：任何复杂的积分问题最终都可以转化为对一个函数求定积分，接下去我将给大家解释，如何计算这一整块面积。（也就是如何计算定积分）

4.2定积分的定义

为了严谨，先给出严格的定积分定义，然后再给出定积分的计算方法。（瞧一瞧看一看啊，非常严谨的定义啊，没有半点水啊，一块钱一斤啊）

（1）定积分的定义

设函数 $f(x)$ 在 $[a,b]$ 上有界（有界就是确保这个函数不会无穷大，都无穷大了我们还算个毛），在 $[a,b]$ 中插入若干个分点

\[a=x_0<x_1<x_2<...<x_{n-1}<x_n=b\\ \]

因此区间 $[a,b]$ 就分成了 $n$ 个小区间

\[[x_0,x_1],[x_1,x_2],...[x_{n-1},x_n]\\ \]

各个区间的长度依次为

\[\Delta x_1=x_1-x_0,\Delta x_2=x_2-x_1,...\Delta x_n=x_{n}-x_{n-1}\\ \]

在每个小区间 $[x_{i-1},x_i]$ 上任取一点 $\xi_i (x_{i-1}\leq\xi_i\leq x_i)$ ，求函数值 $f(\xi_i)$ 与小区间长度 $\Delta x_i$ 的乘积 $f(x_i)\Delta x_i(i=1,2,...,n)$ ，然后求和

\[S=\sum\limits_{i=1}\limits^{n}f(x_i)\Delta x_i\\ \]

记 $\lambda=\max{\{\Delta x_1,\Delta x_2,...\Delta x_n\}}$ ，如果当 $\lambda\to 0$ 时， $S$ 的极限总是存在，且与闭区间 $[a,b]$ 的分法以及点 $\xi_i$ 的取法无关，那么称这个极限为函数 $f(x)$ 在区间 $[a,b]$ 上的定积分（简称积分），记作

\[\int_a^b{f(x)\text{d}x}=\lim\limits_{\lambda\to0}\sum\limits_{i=1}\limits^n{f(\xi_i)\Delta x_i}\\ \]

其中 $f(x)$ 叫做被积函数， $f(x)\text{d}x$ 叫做被积表达式， $x$ 叫做积分变量， $a$ 叫做积分下限， $b$ 叫做积分上限， $[a,b]$ 叫做积分区间。（累死我了）

上面这个定积分的定义是从同济高等数学上摘的，大家就过一遍把它看懂就行了，不用抠字眼，然后拿来烧香供着就好了。（其实这和我之前举的第一个例子相差不大，大家可以对比一下）接下来我将介绍定积分中最重要的公式——牛顿莱布尼茨公式（又名微积分基本定理），没有之一。

4.3牛顿莱布尼茨公式

（1）牛顿莱布尼茨公式

如果 $F(x)$ 是 $f(x)$ 的原函数，那么

\[\int_a^b{f(x)\text{d}x}=F(b)-F(a)\\ \]

【证明】

假设在 $F(x)$ 的 $[a,b]$ 区间中中插入若干个分点

$a=x_0<x_1<x_2<...<x_{n-1}<x_n=b\\$

令

$\Delta x=x_1-x_0=x_2-x_1...=x_{n}-x_{n-1}=\frac{b-a}{n}\\$当 $n\to\infty$ 时，有 $\Delta x$ $\to0$ ，根据导数的定义

$F^\prime(x_i)=\frac{F(x_{i})-F(x_{i-1})}{\Delta x}(\Delta x\to0)\\$ 把 $\Delta x$ 乘过来

$F^\prime(x_i)\Delta x=F(x_{i})-F(x_{i-1})(\Delta x\to0)\\$ 记 $F^\prime(x)=f(x)$ ，并对上式求和

$\sum\limits_{i=1}\limits^{n}f(x_i)\Delta x=\sum\limits_{i=1}\limits^{n}F(x_{i})-F(x_{i-1})\\$ 并且加上极限，大家注意看右边，只剩下了第一项和最后一项

$\lim\limits_{n\to\infty}\sum\limits_{i=1}\limits^n{f(x_i)\Delta x}=F(x_0)-F(x_n)=F(b)-F(a)\\$ 上式的左边即为定积分的求和式，因此我们得到了最终的莱布尼茨公式

$\int_a^b{f(x)\text{d}x}=F(b)-F(a)\\$

这证明确实不太严谨，但比较直观。

注：
① $f(x)$ 需要满足在区间 $[a,b]$ 上连续。
② 这个式子给出了定积分的计算方法：第一步求出原函数，第二步代入积分上下限，第三步相减。高中物理、高中物理竞赛、甚至大学普通物理对于定积分的运用也不会超过牛顿莱布尼茨公式的范畴。
③ 这个公式太完美了，它把求函数与 $x$ 轴面积的问题就轻而易举地解决了，实在是令人敬佩。

（2）积分结果的表示

假设 $F(x)$ 是 $f(x)$ 的原函数，则 $f(x)$ 的定积分的结果有两种表示方法

\[\int_a^b{f(x)\text{d}x}=F(b)-F(a)\\ =F(x)\bigg|_a^b\\ =\bigg[F(x)\bigg]_a^b\\ \]

注：
①上面用一个长竖线的方法是老方法（比较方便），下面这个用一个大的中括号的方法是新方法（比较严谨），两种都可以。大家可以选择与时俱进或者坚持怀旧。

我举个例子看一下牛顿莱布尼茨公式的作用

【例题】计算

\[\int_{-2}^{-1}{\frac{\text{d}x}{x}}\\ \]

【解析】

\[\int_{-2}^{-1}{\frac{\text{d}x}{x}}=\ln{|x|}\bigg|_{-2}^{-1}=\ln1-\ln2=-\ln2\\ \]

不能说是易如反掌，真的就是轻而易举就解决了问题。

五、微分方程

5.1微分方程的定义

未知量为函数，且方程中包含函数的导数的方程。什么意思呢？举个例子， $y^\prime-2x=0$ 就是一个微分方程，我们的目的是求出 $y=y(x)$ 。显然在我举的例子里， $y=x^2$ 就是一个解。

同时微分方程的解并非只有一个，有一个规律：微分方程的最高阶导数是多少阶，最后的通解就有多少个自由变量。在我举的例子里，其实真正的解应该是 $y=x^2+C$ ， $C$ 是一个自由常数。因此微分方程同时存在特解和通解。在物理问题中，通常是根据初始条件来确定这个常数的值，也就是化通解为特解。

3.2可分离变量的微分方程（1）算法举例

拿$y^\prime-2x=0$举个例子，怎么求它的通解？通常我们会把求导写成微商的形式。

\[\frac{\text{d}y}{\text{d}x}=2x\\\]

接下来就是惊天地泣鬼神的一步了，把 $\text{d}x$ 乘到对面去，得到

\[\text{d}y=2x\text{d}x\\ \]

大家可能会有疑问，为什么这个 $\text{d}x$ 可以乘到对面去，前面的一整个式子不就代表了导数嘛？怎么能拆开呢？其实大家可以回想一下微商的基本概念，就是用应变量微分除以自变量微分，所以微商的上下是可以拆开的，他们并不是密不可分的。上面的这个式子其实是用自变量微分代表了应变量微分。（具体的可以看我上一篇文章，在我开头的链接里。）

之后就是对两边的微元求积分（这么说不太严谨，但是比较好理解）

\[\int \text{d}y=\int2x\text{d}x\\ \]

计算结果

\[y=x^2+C\\ \]

上面的是最简单的可分离变量的微分方程计算，接下来我给出可分离变量的微分方程的更加严格的定义

（2）可分离变量的微分方程的定义

一般的，如果一个一阶微分方程能写成

$g(y)\text{d}y=f(x)\text{d}x\\$的形式，也就是说能够把微分方程拆成一边只含 $y$ 和 $\text{d}y$ ，另一边只含 $x$ 和 $\text{d}x$ ，那么原方程就叫做可分离变量的微分方程。

【例题】设一个人背着降落伞从静止的直升机上跳下来，所受空气阻力和速度成正比（ $f=-kx$ ），求人下落速度与时间的函数关系（人的初速度为 $0$）。

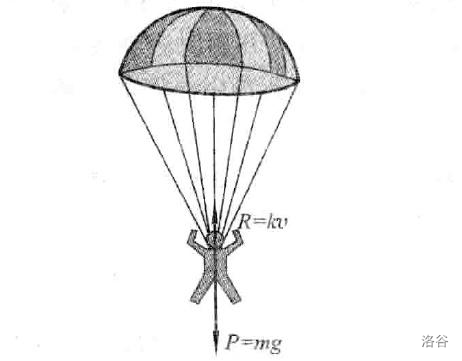
【解析】

受力分析，人和降落伞共受两个力，重力、空气阻力，同时运用牛顿第二定律

\[ma=mg-kv\\\]

把 $a$ 写成微分形式， $a=\frac{\text{d}v}{\text{d}t}$

\[m\frac{\text{d}v}{\text{d}t}=mg-kv\\ \]

分离变量，把右边的 $mg-kv$ 除过来，把 $\text{d}t$ 乘过去，得到

\[\frac{\text{d}v}{g-\frac{k}{m}v}=\text{d}t\\ \]

对两边的微元积分，并且代入初始条件，刚开始 $t=0,v=0$

\[\int_0^v\frac{\text{d}v}{g-\frac{k}{m}v}=\int_0^t\text{d}t\\ \]

积分得到结果

\[-\frac{m}{k}\ln(g-\frac{k}{m}v)\Bigg|_0^v=t\bigg|_0^t\\ \]

即

\[-\frac{m}{k}\ln(g-\frac{k}{m}v)+\frac{m}{k}\ln{g}=t\\ \]

开始化简，A few moments later...

\[\ln(g-\frac{k}{m}v)-\ln{g}=-\frac{k}{m}t\\ \Longleftrightarrow\ln(1-\frac{k}{mg}v)=-\frac{k}{m}t\\ \Longleftrightarrow 1-\frac{k}{mg}v=e^{-\frac{k}{m}t}\\ \Longleftrightarrow v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\\ \]

最终答案

\[v=\frac{mg}{k}(1-e^{-\frac{k}{m}t})\\ \]