526互联

Temporal Point Processes

发布时间 2023-11-09 14:27:50作者: 馒头and花卷

目录

Rasmussen J. G. Lecture notes: Temporal point processes and the conditional intensity function. 2018.

TPP

  • 点过程, 里面的内容感觉和 生存模型 很像.

  • 在日常生活中, 我们常常会遇到和时间相关的事件序列:

    \[h_0=(t_0, \kappa_0), h_1=(t_1, \kappa_1), \ldots, h_n=(t_n, \kappa_n). \]

    其中 \(t\) 表示事件 \(\kappa\) 发生的时间.

  • 一个惯常的任务是, 基于上述的历史信息, 预测下一可能发生的时间 \(\kappa_{n+1}\), 以及它所发生的具体时间 \(t_{n+1}\).

  • 假设没有两个时间在同一时刻发生, 则必有

    \[t_0 < t_1 < \cdots < t_{n} < t_{n+1}. \]

  • 倘若我们用 \(f(\cdot)\) 来表示概率密度, 则有

    \[\tag{1} f(h_0, h_1, \ldots, h_n, h_{n+1}) = \prod_{i=0}^{n+1} f(h_i| \mathcal{H}_{i-1}), \]

    其中 \(\mathcal{H}_{i-1} := [h_0, h_1, \ldots, h_{i-1}]\).

  • 倘若我们能够建模每一个 \(f(h_i |h_{<i})\), 则我们就能够很自然地建模联合概率. TPP 就是这样的一个工具.

Evolutionary point processes

  • 这部分, 我们仅考虑时间的预测, 即建模:

    \[f(t_0, t_1, \ldots, t_{n+1}) = \prod_{i=1}^{n+1} f(t=t_{i} | \mathcal{T}_{i-1}). \]

    其中 \(\mathcal{T}_{i-1} := [t_0, t_1, \ldots, t_{i-1}] = \{t_j \in \mathcal{T}: t_j \le t_{i-1}\}\).

  • 例子 [Renewal process]: 我们以 Renewal Process 这种最简单的随机过程为例. Renewal Process 需要满足: \(\{t_{i} - t_{i-1}\}_{i=1}^{n+1}\) 为独立同分布序列, 即两个事件间的间隔是互相独立且服从统一分布的. 此时我们有:

    \[f(t=t_i|\mathcal{T}_{i-1}) = g(t_i - t_{i-1}), \]

    这里 \(g\) 是某个满足分布条件的密度函数. 比如, 我们可以取 Gamma 分布:

    \[g(\Delta t; \beta, \alpha) = \frac{\beta^{\alpha}}{\Gamma (\alpha)} \Delta t^{\alpha - 1} e^{-\beta \Delta t}. \]

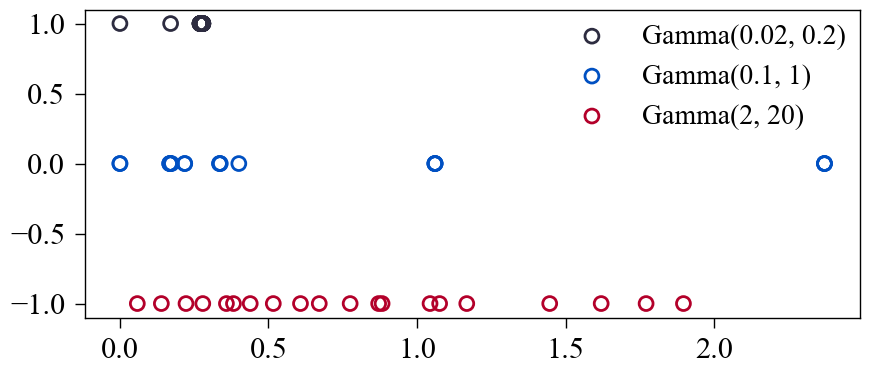
  • 下图是设定不同的 \(\beta, \alpha\) 后的结果 (注意 \(\beta=0.1, \alpha=1\) 实际上是泊松过程).



# %%

import numpy as np
from scipy.stats import gamma
from freeplot import FreePlot

# %%

def sample_from_gamma(beta: float, alpha: float, nums: int = 10) -> float:
    return gamma.rvs(
            a = alpha, scale=1 / beta, size=(nums,)
        )


# %%


nums = 20

fp = FreePlot(
    figsize=(2, 5)
)

# Gamma(0.02, 0.2)
times = np.cumsum(sample_from_gamma(0.02, 0.2, nums))
fp.scatterplot(
    x=times, y=np.ones_like(times) * 1, label='Gamma(0.02, 0.2)', style=['scatter', {'markers.fillstyle': 'none'}]
)

# Gamma(0.1, 1)
times = np.cumsum(sample_from_gamma(0.1, 1, nums))
fp.scatterplot(
    x=times, y=np.ones_like(times) * 0, label='Gamma(0.1, 1)'
)

# Gamma(2, 20)
times = np.cumsum(sample_from_gamma(2, 20, nums))
fp.scatterplot(
    x=times, y=np.ones_like(times) * -1, label='Gamma(2, 20)'
)

fp[0, 0].legend()
fp.show()

Conditional intensity function [\(t\)]

  • 实际中, 往往不似 Renewal process 这般简单, TPP 求助于如下的 conditional intensity function 来确定最终的密度函数 \(f\) (下面的 * 用来强调它是基于 \(\mathcal{T}_{t^-}\) 的):

    \[\lambda^*(t) := \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]| \mathcal{T}_{t^-})}{\Delta t}, \]

    其中 \(\mathcal{T}_{t^-} := \{t_i \in \mathcal{T}: t_i < t\}\). 后面我们令 \(\mathcal{T}_{t_n} = \mathcal{T}_n\).

  • 令,

    \[F(t|\mathcal{T}_{t_n}) = \int_{t_n}^t f(t|\mathcal{T}_{t_n}) dt = \mathbb{P}(t_{n+1} \in [t_n, t]| \mathcal{T}_{t_n}) \]

    为分布函数.

  • 则, 我们有如下关系成立:

    \[\begin{array}{ll} \lambda^*(t) &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]| \mathcal{T}_{t^-})}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]|t_{n+1} \not \in (t_{n}, t), \mathcal{T}_{t_n})}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]|\mathcal{T}_{t_n})}{\Delta t \cdot \mathbb{P}(t_{n+1} \not \in (t_{n}, t)| \mathcal{T}_{t_n})} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]|\mathcal{T}_{t_n})}{\Delta t \cdot \mathbb{P}(t_{n+1} \not \in (t_{n}, t)| \mathcal{T}_{t_n})} \\ &= \frac{1}{1 - F(t|\mathcal{T}_{t_n})} \cdot \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t]|\mathcal{T}_{t_n})}{\Delta t} \\ &= \frac{1}{1 - F(t|\mathcal{T}_{t_n})} \cdot f(t|\mathcal{T}_{t_n}). \\ \end{array} \]

  • 一旦我们确定(或者给定) \(\lambda^*(t)\) (且满足一定的条件), 我们就可以唯一确定 \(f, F\), 注意到

    \[\lambda^*(t) =\frac{f(t|\mathcal{H}_{t_n})}{1 - F(t| \mathcal{T}_{t_n})} =\frac{\frac{\mathrm{d}F(t|\mathcal{H}_{t_n})}{dt}}{1 - F(t| \mathcal{T}_{t_n})} =-\frac{\mathrm{d}}{\mathrm{d}t} \log (1 - F(t|\mathcal{T}_{t_n})). \]

    两边对 \([t_n, t]\) 积分, 得到:

    \[\begin{array}{ll} &-\log (1 - F(t|\mathcal{T}_{t_n})) = \int_{t_n}^t \lambda^*(s) \mathrm{d}s \\ \Rightarrow & F(t|\mathcal{T}_{t_n}) = 1 - \exp(-\int_{t_n}^t \lambda^*(s) \mathrm{d}s) \\ \Rightarrow & f(t|\mathcal{T}_{t_n}) = \lambda^*(t) \exp(-\int_{t_n}^t \lambda^*(s) \mathrm{d}s). \end{array} \]

    注: \(\mathcal{T}_{t_n}\) 建模在 \(*\) 中.

  • \(\lambda^*(t)\) 所满足的条件, 即令所推到得到的 \(f\) 满足密度函数应有的性质:

    1. \(\lambda^*(t)\) 在 \(t > t_n\) 上非负可积;
    2. \(\int_{t_n}^t \lambda^* (s) \mathrm{d}s \mathop{\longrightarrow} \limits^{t \rightarrow \infty} 0\).

Conditional intensity function [\(t, \kappa\)]

  • 这里, 我们同时考虑发生时间和事件, 此时我们类似地定义:

    \[\lambda^*(t, \kappa) := \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa_{n+1} = \kappa| \mathcal{H}_{t^-})}{\Delta t}, \]

    这里 \(\mathcal{H}_{t^-} := \{h_i \in \mathcal{H}: i < t\}\). 注意, 这里我们考虑事件 \(\kappa\) 所属的空间是离散的, 实际上, 连续的也可以 (改成 \(\kappa + \Delta \kappa\)) (但是这里再用区间符号就怪怪的, 但是以离散的眼光审视吧, 结果是一样的).

  • 则, 我们有如下关系成立:

    \[\begin{array}{ll} \lambda^*(t, \kappa) &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa| \mathcal{H}_{t^-})}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa|t_{n+1} \not \in (t_{n}, t), \mathcal{H}_{t_n})}{\Delta t} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa|\mathcal{H}_{t_n})}{\Delta t \cdot \mathbb{P}(t_{n+1} \not \in (t_{n}, t)| \mathcal{H}_{t_n})} \\ &= \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa|\mathcal{T}_{t_n})}{\Delta t \cdot \mathbb{P}(t_{n+1} \not \in (t_{n}, t)| \mathcal{H}_{t_n})} \\ &= \frac{1}{1 - F(t|\mathcal{H}_{t_n})} \cdot \lim_{\Delta t \rightarrow 0} \frac{\mathbb{P}(t_{n+1} \in [t, t + \Delta t], \kappa|\mathcal{H}_{t_n})}{\Delta t} \\ &= \frac{1}{1 - F(t|\mathcal{H}_{t_n})} \cdot f(t, \kappa|\mathcal{H}_{t_n}). \\ &= \frac{1}{1 - F(t|\mathcal{H}_{t_n})} \cdot f(t|\mathcal{H}_{t_n}) \cdot f(\kappa|t, \mathcal{H}_{t_n}) \\ &= \lambda^*(t) \cdot f^*(\kappa|t). \end{array} \]

    这里我们定义 \(f^*(\kappa|t) := f(\kappa|t, \mathcal{H}_{t_n})\).

  • 换言之, 我们只要确定 \(\lambda^*, f^*\) 即可确定发生时间 + 发生时间的随机过程.

Inference

  • 我不清楚为什么不直接确定 \(f\) 而需要一个跳板 \(\lambda^*\), 想必是它在推理和抽样上具有特别的性质.

  • 很多时候, 我们需要通过极大似然来拟合模型, 所以似然函数的计算是一个比较重要的问题. 假设我们在 \([0, T]\) 时间段内观测到 \([(t_0, \kappa_0), \ldots, (t_n, \kappa_n)]\), 下面介绍其上的似然函数的计算.

  • 定义:

    \[\Lambda^*(t) = \int_0^t \lambda^*(s) \mathrm{d}s. \]

  • 根据 (1) 可得:

    \[L = (1 - F(T|\mathcal{H}_{t_n})) \cdot \prod_{i=0}^{n+1} f(h_i| \mathcal{H}_{i-1}) \]

    比较特别的是 \((1 - F(T|\mathcal{H}_{t_n}))\), 即我们可以确定, \(t_{n+1}\) 一定发生在 \(>T\) 的时间段内.

  • 于是, 我们有:

    \[L = \bigg( \prod_{i=0}^n \lambda^*(t_i) \bigg) \bigg( \prod_{i=0}^n f^*(\kappa_i| t_i) \bigg) \exp \bigg(-\int_0^T \lambda^*(s) \mathrm{d}s \bigg). \]

Simulation

Inverse Method

  • 假设序列 \([s_0, s_1, \ldots, t_n]\), 我们有序列 (假设 \(\Lambda^*\) 可逆)

    \[[s_0= \Lambda^*(t_0), \ldots, s_n = \Lambda^*(t_n)] \]

    服从 unit rate Poisson process. 即

    \[f(s_i|s_{i-1}, \ldots, s_{0}) = f(s_i|s_{i-1}) = e^{-(s_i - s_{i-1})}, \quad s_i > s_{i-1}. \]

    即间隔时间是互相独立的 (且服从 \(\lambda=1\) 的泊松分布).

  • 我们有

    \[\begin{array}{ll} F(s|\mathcal{H}_{s_n}) &= \mathbb{P}(s_{n+1} \le s| s_{n}, \ldots, s_0) \\ &= \mathbb{P}(\Lambda^*(t_{n+1}) \le s| t_{n}, \ldots, t_0) \\ &= \mathbb{P}(\Lambda^*(t_{n+1}) \le s| \mathcal{H}_{t_n}) \\ &= \mathbb{P}(t_{n+1} \le \Lambda^{*-1}(s)| \mathcal{H}_{t_n}) \\ &= F(\Lambda^{*-1}(s)| \mathcal{H}_{t_n}) \\ &= 1 - \exp(- \int_{t_n}^{\Lambda^{*-1}(s)} \Lambda^*(t) \mathrm{d}t) \\ &= 1 - \exp\bigg(- \big(\Lambda^*(\Lambda^{*-1}(s)) - \Lambda^*(t_n) \big)\bigg) \\ &= 1 - \exp\bigg(- \big(s - s_n \big)\bigg) \\ &= \int_{s_n}^s \exp(-t) \mathrm{d}t. \\ \end{array} \]

    故成立.

  • 同理, 如果 \([s_0, s_1, \ldots, s_n]\) 服从 unit rate Poisson process, 则

    \[[t_0 = \Lambda^{*-1}(s_0), \ldots, t_n=\Lambda^{*-1}(s_n)] \]

    服从密度函数为 \(\lambda^*\) 的点过程.

  • 如此一来, 我们想要从该过程中抽样, 只需要先从 unit rate Poisson process 中抽样然后再做变换即可.

Ogata’s modified thinning algorithm

  • 这部分没看明白, 有兴趣的可以回看原文.

例子

  • Hawkes process: 它的密度函数定义为:

    \[\lambda^*(t) = \mu + \alpha \sum_{t_i < t} \exp(-(t - t_i)), \]

    我们可以得到:

    \[\begin{array}{ll} \Lambda^*(t) &=\int_0^t \lambda^*(s) \mathrm{d}s \\ &=\int_0^t \mu + \alpha \sum_{t_i < s} \exp(-(s - t_i)) \mathrm{d}s \\ &=\mu t + \alpha \int_0^t \sum_{t_i < s} \exp(-(s - t_i)) \mathrm{d}s \\ &=\mu t + \alpha \sum_{t_i < t} \int_{t_i}^t \exp(-(s - t_i)) \mathrm{d}s \\ &=\mu t + \alpha \sum_{t_i < t} \bigg(1 - \exp(-(t - t_i)) \bigg). \\ \end{array} \]

  • 可惜的是, \(\Lambda^{*-1}\) 没有显式解, 一个近似策略是:

    1. 采样 \([s_0, s_1, s_2, \ldots]\);
    2. \(t\) 从 \(0\) 开始逐步增加, 一旦

      \[\Lambda^*(t) \approx s_0 \Rightarrow t_0 \approx t, \]

      然后继续进行逐步得到 \(t_1, t_2, \ldots\).

  • 上图是在 \(\mu=0.5, \alpha=0.9\) 的情况下采样的 20 个点, 以及所对应的 \(\lambda^*(t)\) 的可视化. 可以发现, Hawkes process 有这样的性质: 在 \(t_i\) 处倘若发生了事件, 则 \(t_i + \Delta t\) 一个时间内发生的概率往往会变大, 从而更容易出现聚合的效应.

  • 下面是代码:


# %%

import numpy as np
from scipy.stats import gamma
from freeplot import FreePlot

# %%

def sample_from_gamma(beta: float, alpha: float, nums: int = 10) -> float:
    return gamma.rvs(
            a = alpha, scale=1 / beta, size=(nums,)
        )


def hawkes_conditional_intensity_function(t, ts: list, mu: float, alpha: float):
    # \lambda^*(t)
    ts = np.array(ts)
    ts = ts[ts < t]
    return mu + alpha * np.sum(np.exp(ts - t))

def hawkes_integrated_conditional_intensity_function(t, ts: list, mu: float, alpha: float):
    # \Lambda^*(t)
    ts = np.array(ts)
    return mu * t + alpha * np.sum(1 - np.exp(ts - t))

# %%



nums = 20
mu = 0.5
alpha = 0.9
step_size = 0.01

ss = np.cumsum(sample_from_gamma(1, 1, nums))
ts = []
t = 0

for s in ss:
    s_hat = hawkes_integrated_conditional_intensity_function(
        t, ts, mu, alpha
    )
    while s_hat < s:
        t += step_size
        s_hat = hawkes_integrated_conditional_intensity_function(
            t, ts, mu, alpha
        )
    ts.append(t)

points = np.linspace(0, ts[-1] + 1, 100)
densities = [
    hawkes_conditional_intensity_function(
        point, ts, mu, alpha
    ) for point in points
]

fp = FreePlot(
    figsize=(2, 5)
)

fp.scatterplot(
    x=ts, y=np.zeros_like(ts), style=['scatter', {'markers.fillstyle': 'none'}]
)

fp.lineplot(
    points, densities, marker=''
)

fp.show()