摘要： 首先给出刚体被控对象的微分方程，然后对四元数微分方程线性化求出合适的PD控制参数，然后详细分析了误差四元数的概念和性质，并提出四元数和旋转矩阵的等价性，然后简要介绍了非对角转动惯量矩阵的一些特点，最后分别仿真验证了调节问题、跟踪问题和误差四元数，附录中给出了使用拉塞尔不变性原理证明PD控制稳定性的过程。

被控对象建模

  首先列出被控对象的微分方程。在此之前先提一下坐标系，常用的就两个，一个是固定于地面的世界系，另一个是固定在无人机（或称刚体）上的本体系。被控对象的微分方程如下

上面两式分别称作刚体姿态动力学方程和运动学方程。第一行的动力学方程中，\(J\) 是刚体在本体系下的转动惯量（注意不是世界系下，除了四元数是本体系相对于世界系以外，其它变量都是在本体系下描述），\(\vec w\) 是刚体在本体系下的角速度向量，\(\vec M\) 是刚体在本体系下所受的力矩向量。第二行的运动学方程中，\(Q\) 是刚体在世界系下的姿态四元数，\(\circ\) 表示四元数乘法。这两个微分方程就描述了刚体从力矩到姿态的变化过程。这两个方程的进一步细节分析可以看我之前的推导笔记
姿态运动学：角速度变化时四元数和旋转矩阵微分方程的证明
姿态动力学：刚体姿态动力学推导与进动现象仿真
  实际上(1)式应该是最正规的建模公式，其它建模方法都不够简洁，可以看 为何三维旋转只有三个自由度却用四元数来表示？-找不到服务器的回答 -知乎 中我和其他人的回答，航模和无人机中也都是使用四元数控制，并针对绕偏航轴的特殊性使用了“倾转分离”的算法，但我暂时还没仔细研究过。

线性化设计控制律

  控制问题分为调节问题和跟踪问题。调节问题指的是，没有外部输入，设计一个状态反馈使系统稳定到平衡点；跟踪问题就是常见的使系统状态跟踪指令输入。严格的定义参考一下专业书。
  使用拉塞尔不变集原理可以证明，四元数PD控制中取任意大于0的PD参数都可以让刚体从任何状态回到初始位置。我看完了证明过程仍然觉得这很不可思议，但前提是控制律也得是连续的，而实际中控制器都是离散的。证明过程贴到最后面。
  尽管任意PD参数都可以保证稳定，但控制效果就不一定能保证了，下面计算合适的PD参数。在平衡点附近线性化，平衡点为 \(\vec w=\vec 0,Q=[1,0,0,0]\)，

因为 \(\dot\epsilon\) 中不含输入力矩，所以对 \(\dot\epsilon\) 再次求导并忽略高阶项

如果 \(J\) 为对角阵，那么向量形式可以简单地拆开成三个轴分别设计参数

即可根据极点配置法分别确定3轴PD参数。

跟踪问题

  前面设计了调节问题的控制律参数，下面研究跟踪问题。跟踪问题需要引入误差四元数的概念，可以看下面这篇论文

E. Fresk and G. Nikolakopoulos, "Full quaternion based attitude control for a quadrotor," 2013 European Control Conference (ECC), Zurich, Switzerland, 2013, pp. 3864-3869, doi: 10.23919/ECC.2013.6669617.

定义误差四元数为 \(Q_e=Q_0\circ Q^{-1}\)（这个好像不对，等我后面确认一下），其中 \(Q_0\) 为期望姿态四元数，\(Q\) 是当前姿态四元数，然后利用四元数的性质，四元数的虚部是旋转轴和旋转角度（具体见 如何形象地理解四元数？-知乎 或其他类似博客），利用姿态误差和角速度设计PD控制

其中 \(w_x, w_y, w_z\) 为三轴角速度分量，\(q_1, q_2, q_3\) 为误差四元数的虚部。根据转动惯量矩阵的实际值，三个轴的PD参数 \(k_p,k_d\) 可以不同。

跟踪问题中误差四元数的原理

  再深究一下误差四元数的定义，误差四元数为什么是

而不是下面这3种？

定义函数 \(R(Q)\) 表示把一个四元数转换成旋转矩阵，有下面一些性质

（这个式子的证明见 证明四元数乘法与旋转矩阵乘法等价）所以可以类似地转换成误差旋转矩阵 \(R_e=R_0R^{-1}\)，
问题就成了，怎样把当前的姿态旋转矩阵旋转到期望旋转矩阵。前面在线性化的时候把平衡点选到了 \(Q=[1,0,0,0]\) 处（后面称这个姿态为"零姿态"），如果期望姿态不在这里，那就在期望姿态处新建一个坐标系，称作期望系，使期望姿态为零姿态。此时，期望系到世界系的旋转矩阵为 \(R_0\)，本体系到世界系的旋转矩阵为 \(R\)，那么本体系到期望系的旋转矩阵就是 \(R_0^{-1}R\)。因为误差四元数中自带负号，相当于旋转矩阵求逆，所以等价的误差旋转矩阵为 \(R_e=R^{-1}R_0\)，对应的误差四元数为

  除此以外还有另外一种理解方式。已知，对一个旋转矩阵左乘旋转矩阵相当于把刚体绕世界系旋转，右乘相当于绕本体系旋转（具体解释可以看我之前写的笔记 自用的四元数、欧拉角、旋转矩阵笔记 的最后一节“xyz固定角和zyx欧拉角相等的直观理解”）
而力矩是在本体系下描述的，所以需要右乘，将本体系相对于世界系的旋转矩阵 \(R\) 右乘误差旋转矩阵 \(R_e\) 得到期望旋转矩阵 \(R_0\)，于是 \(RR_e=R_0\)，\(R_e=R^{-1}R_0\)，也可以得到等价的误差四元数。
  实际仿真中分别试了4种情况，分别为正确的误差四元数和式(3)中表示的另外3种情况，发现都能达到期望姿态，但是正确的误差四元数的过渡过程是最快的。仿真代码和结果见下文“跟踪问题仿真”一节。

非对角矩阵

  转动惯量矩阵是正定矩阵，证明见 Positive Definiteness of the Moment of Inertia Tensor 当转动惯量矩阵不是对角阵时，需要取线性变换转换成对角阵。取 \(\vec\alpha=C\vec\epsilon\)，于是

变为

取合同变换矩阵 \(C\) 使 \(CJ^{-1}C^{-1}\) 为对角阵。合同变换结果不唯一， \(C\) 的取值既影响 \(k_p,k_d\) 参数，也通过 \(\vec\alpha\) 影响 \(\vec\epsilon\) 的稳定性。感觉 \(C\) 的取值类似于选择合适的传递函数零点，虽然不影响稳定性，但影响收敛速度。
合同变换方法见 请问求二次型的标准型的三种方法？

调节问题仿真

被控对象如下。其中 quaternions.py 的代码见 自用的四元数、欧拉角、旋转矩阵转换代码。
这个被控对象也在后面的仿真中使用。

# rigidbody.py
# 四阶龙格库塔法建立刚体的运动学和动力学模型
import numpy as np
from quaternions import *

# 默认控制律，没有期望姿态
def Control_Law(state):
    Qv, W = state[1:4], state[4:7]
    return -np.array([2, 20, 6])*Qv -np.array([2, 20, 6])*W

# 刚体
# J: 刚体的转动惯量矩阵
# initEuler: 刚体的初始欧拉角
# initOmega: 刚体的初始角速度向量
class RigidBody:
    def __init__(self, J, initEuler, initOmega):
        self._J = J
        e1 = initEuler
        w1 = initOmega
        self._t = 0
        self._Jinv = np.linalg.inv(self._J)
        q1 = Euler_To_Quaternion(e1)
        self._states = np.concatenate((q1, w1), dtype=float)
        self.ctrlLaw = Control_Law  # 默认控制律

    def Simulate_OneStep(self):
        h = 0.01
        K1 = self._ODE4Function(self._t, self._states)
        K2 = self._ODE4Function(self._t+h/2, self._states + h/2*K1)
        K3 = self._ODE4Function(self._t+h/2, self._states + h/2*K2)
        K4 = self._ODE4Function(self._t+h, self._states + h*K3)
        dx = h/6*(K1 + 2*K2 + 2*K3 + K4)
        self._states += dx

    def Get_State(self):
        return self._states
    def Get_QuaternionVec(self):
        return Quaternion_to_Euler(self._states[0:4])

    def _ODE4Function(self, t, x):
        Qs, Qv, W = x[0], x[1:4], x[4:7]
        dQs = -0.5*np.dot(Qv, W)
        dQv = 0.5*(Qs*W + np.cross(Qv, W))
        torque = self.ctrlLaw(x)
        dW = self._Jinv @ (torque - np.cross(W, self._J @ W))[0]
        return np.concatenate((np.array([dQs]), dQv, np.array(dW)[0]))

主程序代码如下。

# main.py
import numpy as np
import matplotlib.pyplot as plt
from rigidbody import RigidBody
J = np.matrix([
            [1, 0, 0],
            [0, 10, 0],
            [0, 0, 3],
])
usv1 = RigidBody(J, np.array([1, -0.2, 0.3]), np.array([-0.1, 0.2, -3]))
t = 0
plottime, ploteuler = [], []
plottime.append(t)
ploteuler.append(usv1.Get_QuaternionVec())
while 1:
    for n in range(10):
        usv1.Simulate_OneStep()
    t += 0.1
    plottime.append(t)
    ploteuler.append(usv1.Get_QuaternionVec())
    if t > 10:
        break
pass
print(ploteuler[-1])
plt.plot(plottime, ploteuler)
plt.legend(['roll', 'pitch', 'yaw'])
plt.show()

仿真结果如下

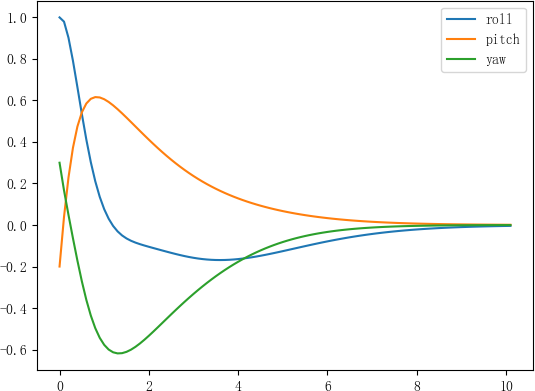
跟踪问题仿真

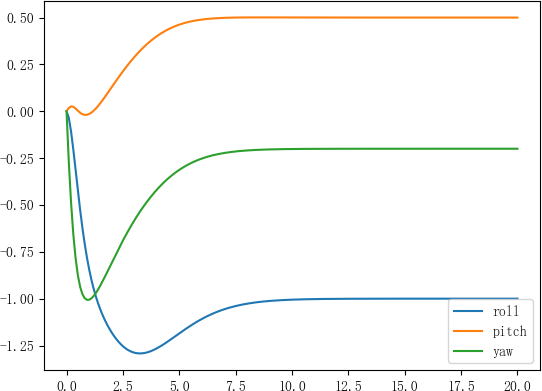
期望姿态角分别为 \(-1, 0.5, -0.2\)。

import numpy as np
import matplotlib.pyplot as plt
from quaternions import *
from rigidbody import RigidBody

def Control_Law(state):
    Qcurrent, omega = state[0:4], state[4:7]
    Qerr = Quaternion_Product(Quaternion_Inverse(Qcurrent), Qtarget)  # +
    # Qerr = Quaternion_Product(Quaternion_Inverse(Qtarget), Qcurrent)  # -
    # Qerr = Quaternion_Product(Qtarget, Quaternion_Inverse(Qcurrent))  # x
    # Qerr = Quaternion_Product(Qcurrent, Quaternion_Inverse(Qtarget))  # x
    torque = np.array([2, 20, 6])*Qerr[1:4] -np.array([2, 20, 6])*omega
    return torque

J = np.matrix([
            [1, 0, 0],
            [0, 10, 0],
            [0, 0, 3],
])
Qtarget = Euler_To_Quaternion(np.array([-1, 0.5, -0.2]))
usv1 = RigidBody(J, np.array([0, 0, 0]), np.array([-0.1, 0.2, -3]))
usv1.ctrlLaw = Control_Law
t = 0
plottime, ploteuler = [], []
plottime.append(t)
ploteuler.append(usv1.Get_QuaternionVec())
while 1:
    for n in range(10):
        usv1.Simulate_OneStep()
    t += 0.1
    plottime.append(t)
    ploteuler.append(usv1.Get_QuaternionVec())
    if t > 20:
        break
pass
print(ploteuler[-1])
plt.plot(plottime, ploteuler)
plt.legend(['roll', 'pitch', 'yaw'])
plt.show()

其中控制律代码中列出了4种误差四元数，后面分别有+-xx的注释，+表示控制律为

torque = np.array([2, 20, 6])*Qerr[1:4] -np.array([2, 20, 6])*omega

-表示控制律为

torque = -np.array([2, 20, 6])*Qerr[1:4] -np.array([2, 20, 6])*omega

x表示结果不正确，但也能逐渐过渡到期望姿态。标+-两种情况的仿真结果相同，如下图所示

标xx的两种情况分别为


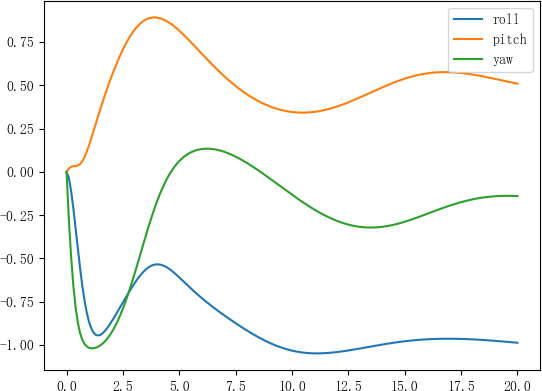
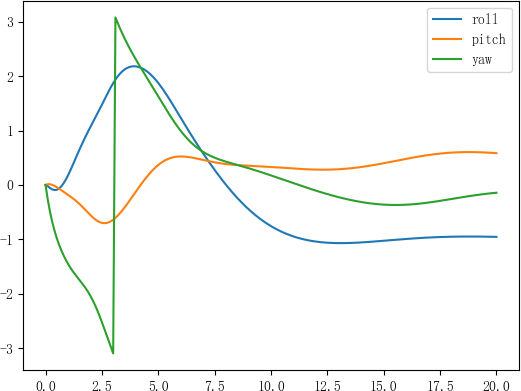
并且同样的原理，改了控制律中-np.array([2, 20, 6])前面的正负号后，上面两种结果交换顺序后完全相同。

附录

这一节讲下面这本书的第24章里介绍的方法，使用拉塞尔不变集原理证明PD控制稳定性。

De Ruiter. Spacecraft dynamics and control: an introduction. 2013.

拉塞尔不变集原理

一个多输入多输出非线性系统

定义 \(x\) 的解为集合 \(D\)，再定义一个 \(x\) 的有界闭集 \(\Omega\) 为当 \(t\geq 0\) 时，\(x(t)\in\Omega\)。令 \(V(\vec x):D\to\mathbb R\) 为一个连续可微函数并满足 \(\dot V\leq 0\)，定义集合 \(E\) 为 \(\dot V(\vec x)=0\) 时 \(\vec x\) 的集合。令 \(M\) 为 \(E\) 中的最大不变集，那么当 \(t\to\infty\) 时，\(\vec x(t)\to M\)。

运用拉塞尔不变集原理的步骤为

1. 构造能量函数V，可以不是正定函数。
2. 求能量函数的时间一阶导数，判断是否 \(\dot V(x)\leq 0\)。如果不满足，需要重新构造。
3. 令 \(\dot V=0\)，求子集 \(E\)。
4. 判断子集 \(E\) 中的不变集，找出最大的不变集 \(M\)。

关于拉塞尔不变集更详细的解释建议参考khaill的《非线性系统》。
拉塞尔不变集原理解读（包含径向无界性的解读）
关于LaSalle不变集定理的一个问题
非线性与自适应控制（三）LaSalle Invariance Principle
关于开集、闭集、紧集可以参考
【最优化】几何概念概述
小白拓补学｜4. 究竟什么是紧集(compact set)？

证明PD控制稳定性

  把四元数的标量和向量部分分别记作 \(\eta\) 和 \(\vec\epsilon\)，于是被控对象可以写作

设计控制律

代入姿态动力学方程得到

考虑能量函数

求导

然后求不变集。因为单位四元数满足

所以

假设转动惯量矩阵的3个主惯量轴满足

于是

其中 \(V_0=V(\eta(0),\vec\epsilon(0),\vec w(0))\)，于是

\(\Omega\) 中的子集 \(E\) 为 \(\dot V=0\) 时 \(\vec x\) 的集合，即 \(\vec w=0\)

下面求最大不变集，将 \(\vec w=0\) 代入被控对象式(A.1)得

因为 \(\vec w=0\)，所以 \(\dot{\vec w}=0,\vec\epsilon=0\)，由单位四元数的性质得 \(\eta=\pm 1\)，所以最大不变集

这就是刚体最后稳定的状态。
  前面的推导中假设了转动惯量矩阵是对角阵，如果不是对角阵的话，实际的系统的转动惯量矩阵一定是正定矩阵，那么可以经过线性变换转换成正定的对角阵，也可以类似得到 \(\vec w\) 的范围。具体细节有待进一步推导。

本栏目推荐文章
• 根据语音生成全身姿态；基于变分贝叶斯框架的VAE模型；CFG是一种隐式的Perceptual Loss！
• 打开CodeReview新姿态
• MoveNet：超快且准确的姿态检测模型
• 任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的
• 刚体四元数姿态控制
• 浅谈AI人体姿态识别技术的先进性及安防视频监控应用场景
• 2D物理引擎 Box2D for javascript Games 第四章 将力作用到刚体上
• 姿态估计入门
• 互补滤波姿态解算算法思路
• openvino头部姿态识别

刚体 姿态刚体 动力学 姿态 动力 刚体 姿态 空间6050 刚体 姿态 刚体 矩阵 刚体 是由 三个 姿态 刚体 墙体 自动生成 上层 刚体alphafold2 alphafold 刚体 力作javascript物理 realsense姿态 相机 数据