数论 结论

# Mod ## 一、long long 乘法取模 #### 核心思想 用long double 估计商的取值，然后任它溢出,它的真实答案和它%$2^{64}$次方答案是一样的 $x*y$%$m = x*y-\dfrac{x*y}{m}*m$ #### 代码 ```c++ ll mul(ll x,l ......

# Combinatorial Number ## 一、[组合数取模1：](http://oj.daimayuan.top/course/12/problem/524) #### 例题：回答T组询问，输出$C_{n}^{m} \bmod 10^9+7$的值。 $C_{n}^{m} = \dfrac{ ......

# Chinese Remainder Theorem $x≡ai(mod mi)$ **中国剩余定理CRT** ## 1.定义 **Th.** 给出一元线性同余线性方程组 $x ≡ a1 \bmod m1$ $x ≡ a2 \bmod m2$ ... $x ≡ an \bmod mn$ 定理指出假 ......

# Prime sieving and Integer blocking ## 一、Prime number sieve method ### 1.埃氏筛O(nloglogn) 从 2 开始，2是质数，那么2的倍数：4、6、8、10、12、14、16... 肯定不是质数 3是质数，那么3的倍数：6、 ......

## Divisor and Gcd ### 1、算术基本定理：n的质因数分解唯一 一些常见结论： 1.素数无限 2.$\lim_{n\rightarrow+\infty}n\prod\dfrac{n}{\frac{n}{\ln{n}}}$(Π(n)表示 ab|c$ 3.$a|bc,(a,b) = ......

## 数论 ### 小知识复习 整除、质数、线性筛、 $gcd$ 、 $exgcd$ 、逆元、快速幂、费马小定理、（扩展）欧拉定理、卢卡斯定理、中国剩余定理、原根、常见数论函数…… 给一张比较有用的表： ![image](https://img2023.cnblogs.com/blog/304896 ......

比较难,没怎么看懂 //约数: //如果一个数d是n的一个约数,即d能整除n,那么n/d也能整除n: //求所有约数(除法求约数,o(sqrt(n))) #include<bits/stdc++.h> using namespace std; const int N=1e5+10; int n,x; ......

# 巴塞尔级数的一个小结论 已知 $$ \sum_{n=1}^{\infty}\frac{1}{n^2}=\frac{1}{1^2}+\frac{1}{2^2}+\cdots=\frac{\pi^2}{6} $$ 经过运算得 $$ \left(1-\frac{1}{2^2} \right )\sum ......

# 前置知识 ## 积性函数 满足 $f(1)=1$，并且当 $\gcd(a,b)=1$ 时，有 $f(ab) = f(a)f(b)$，则称 $f(n)$ 为积性函数。 如果对于全部的 $a,b$，都有 $f(ab)=f(a)f(b)$，则称 $f(n)$ 是完全积性函数。 ### 常见积性函数 1 ......

// 最基本求一个素数(on),(osqrt(n)) #include<bits/stdc++.h> using namespace std; int main() { int n; cin>>n; for(int i=2;i<n;i++)//o(n) if(n%i==0){ cout<<"no"; ......

# GCD&LCM&欧拉函——推柿子 ## 一、$\sum_{i = 1}^{n}[\gcd(i,n)=d]$ $\sum_{i = 1}^{n}[\gcd(i,n)=d]$ $=\sum_{i = 1}^{\frac{n}{d}}[\gcd(i,\frac{n}{d})=1]$ $=\phi(\f ......

下面这个结论，记住就可以了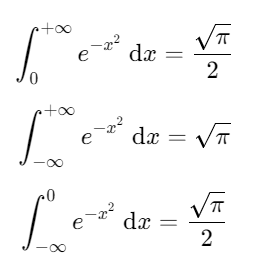：  ## [详情点这里](https://zhaokaifeng.com/15439/ ......

### 求和符号的定义 为了简化形如 $a_1+a_2+...+a_n$ 这样求 $n$ 个数的和的表述，引入求和符号 $\sum$，将上式重表述为 $\sum\limits_{i=1}^na_i$。 其中，$i$ 被称为指标变量，取值为从 $1$ 到 $n$ 的整数，$a_i$ 为关于 $i$ 的 ......

# 1.【最大公约数（GCD）和最小公倍数（LCM）】 ## 【基本性质、定理】 * $\large gcd(a,b)=gcd(b,a−b) (a>b)$ * $\large gcd(a,b)=gcd(b,a$ $\large mod$ $b)$ * $\large gcd(a,b)$ $\larg ......

## 结构1 > 已知抛物线 $y = ax^2$，直线 $AB$ 经过点 $M(0,t)$ 与抛物线交于点 $A、B$ 两点，连接 $AO$ ,过点 $B$ 作 $BC \parallel y$ 轴交直线 $AO$ 于 $C$, C点的纵坐标: $y_c=-t$ 证明： 设 $l_{ab}:y=k ......

## 裴蜀定理 对于任意的整数a、b，都存在一对整数x、y（注意x和y可以是负整数），使得$ax+by = gcd(a,b)$成立。或者可以这样描述：对方程$ax+by = c，(a,b,c∈Z)$，只有满足$gcd(a,b)|c$（即a和b的最大公约数可以整除c），方程才有整数解。 ## 扩展欧几 ......

## 取模 $$ (1) \quad 5 \div 3 = 1 \cdots 2\\ a = b \cdot c + d\\ (2) \quad a \div b = c \cdots d\\ b > d \ge 0\\ (3) \quad a, b, c = a / b, d = a \bmod ......

# 未完工。 目前咕掉的： 卢卡斯定理 ~~真正有用的一个没有~~ # 质数： 威尔逊定理：$p$ 为质数的充要条件为 $(p-1)!\equiv -1\pmod p$ 证明： $1.$ 充分性： 反证，假设 $p$ 是合数。 如果 $p$ 为质数的平方，例如 $p=4$，则 $3!\equiv 2 ......

# 前言 关于高次同余方程，有 $a^x \equiv b(\text{mod} \ p)$ 和 $x^a \equiv b(\text{mod} \ p)$ 两种类型，后者计算起来较为麻烦，下文就分别记述这两种高次同余方程。 # 离散对数问题 离散对数问题是在模 $p$ 意义下求解 $\log_a ......

 参考：https://www.cnblogs.com/alex-wei/p/Number_Theory.html ......

 参考：https://www.cnblogs.com/alex-wei/p/Number_Theory.html ......

## 线性筛素数 直接上代码。 ```cpp const int MAXN=100000008; bool np[MAXN]; vector prm,pre; void gg(const int N=100000000){ pre.resize(N+1); for(int i=2;i 积性：如果对于 ......

# 排列组合 > 排列就是指从给定个数的元素中取出指定个数的元素进行排序；组合则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。 OI Wiki ### 乘法原理和加法原理 加法原理，就好比一个工作，有 $n$ 个解决的方案，第 $i$ 项方案有 $a_{i}$ 种不同的实现方式，所以这个 ......

# 题目地址 https://ac.nowcoder.com/acm/contest/57677/A # 代码 ``` use std::io::{self, BufRead, Write}; fn is_prime_triival(n: i128) -> bool { if n i128 { le ......

# 前言 在学习本节内容前，最好先学习[同余的基本性质](https://www.luogu.com.cn/blog/157884/tong-yu-di-ji-ben-xing-zhi)以加深理解。 # 一堆定理 * 定理1： **若** $$a,b,m,n \in \mathbb Z,c \mid ......

# 前言 在学习本节内容前，请确保已完成了[同余方程](https://www.luogu.com.cn/blog/157884/basic-math-note-2)的学习。 # 模的逆 ## 引入 很多题目都会要求我们对答案取模。 如果运算中只有加法、乘法当然没问题。 但是如果有除法就完蛋了。 所 ......

# 前言 在学习本节内容前，请确保已完成了[二元不定方程](https://www.luogu.com.cn/blog/157884/basic-math-note)的学习。 # 同余方程 ## 有无解的判别 对于一个方程形如： $$ax \equiv b \pmod m$$ 其中 $$a,b \i ......

整除 设 $a,b\in \mathbb{Z},a\ne 0$。如果 $\exists q\in \mathbb{Z}$，使得 $b=a\times q$，那么就说 $b$ 可被 $a$ 整除，记作 $a\mid b$ ；$b$ 不被 $a$ 整除记作 $a\nmid b$ 。 OI Wiki 整除 ......

AtCoder abc230_e AtCoder abc230_e Fraction Floor Sum 求: $$\sum_{i = 1}^N ⌊\dfrac{N}{i}⌋$$ P2261 [CQOI2007]余数求和 P2261 [CQOI2007]余数求和 $$G(n, k) = \sum_{ ......

最近打算学计数DP，然而我数学基础太弱，故记此文。（问了一下，这东西只不过是小学奥数而已，我好蒻） 公式 加法原理：$ S= \sum_{i=1}^n a[i] $ 乘法原理：$ S= \prod_{i=1}^n a[i] $ 二项式定理：$(a+b)^n = \sum_{i=0}^n a^{n-i ......