平行四边形
dp优化-决策单调性 / 四边形不等式
前言 这种优化我以前“听”过了很多次,但是好像都没学会qwq。 四边形不等式: 对于二元组 \(w_{x,y}\),如果在定义域上任取四个点 \(a \le b \le c \le d\),满足: \[w_{a,b}+w_{c,d} \ge w_{a,c}+w_{b,d} \]则称 \(w_{x,y ......
[转]电子对抗作战任务规划:战场平行仿真系统
本文转自:微信公众号 军桥网 作战任务规划来源于美军,所对应的英文为“Operation Planning /Mission Planning”,此“Operation Planning(OP)”与“Mission Planning(MP)”是一个整体。美军对“OP”与“MP”均有详细定义,前者指战 ......
Next.js 开发指南 路由篇 | 动态路由、路由组、平行路由和拦截路由
前言 实际项目开发的时候,有的路由场景会比较复杂,比如数据库里的文章有很多,我们不可能一一去定义路由,此时该怎么办?组织代码的时候,有的路由是用于移动端,有的路由是用于 PC 端,该如何组织?如何有条件的渲染页面,比如未授权的时候显示登录框?如何让同一个路由根据情况不同展示不同的内容? 本篇我们会一 ......
240104 杂题全谈 四边形不等式
因为输入法没有给我满意的候选项所以这次就不取抽象标题了。 可恶每道题还要证明一下满足四边形不等式,真是难为我了。 A - Chef and Bitwise OR Operation https://vjudge.net/contest/602275#problem/A CodeChef - CHEF ......
<学习笔记> 四边形不等式
四边形不等式 对于任意的 \(l_1\le l_2\le r_1\le r_2\),满足 \(w(l_1,r_1)+w(l_2,r_2)\le w(l_1,r_2)+w(l_2,r_1)\) 。 若等号恒成立,则称函数 \(w\) 为四边形恒等式。 如何证明 若满足 \(w(l,r-1)+w(l+1 ......
复杂一点的四边形不等式和邮局
四边形不等式不仅在一维的线性dp中可以使用,在二维dp中也是很不错的东西 这个二维dp不局限于区间dp,虽然四边形不等式优化石子合并是很经典的东西 但是这种四边形不等式我不打算推导,而是直接背结论,因为我觉得知道推导过程对我的作用不是很大而且麻烦 在区间dp问题中,这样的方程\(f[i][j]=\d ......
诗人小G和四边形不等式
对于线性的dp \(f[i]=min(f[j]+val(i,j))\) 或者说是大致的转移方程可以写成这样的dp,时间复杂度大概是\(O(n^2)\) 能否优化主要取决于\(val(i,j)\)的内容和\(j\)的范围 假如\(j\)的范围是一个单调向后移动的窗口,只要\(val(i,j)\)能够用 ......
将向量提取器用于平行语料对齐的一个小示例
from sentence_transformers import SentenceTransformer import numpy as np from os import path model_path = ( '/data/m3e-base' if path.isdir('/data/m3e- ......
四边形不等式笔记
说明 设 \(w(x,y)\) 是定义在整数集合上的二元函数。 下文所有数都在默认的定义域上。 下文的四边形不等式定义是对于决策单调性函数中决策函数为 \(\min\) 而言的。如果要求考虑决策函数为 \(\max\) ,则需要将下文中的关于 \(w\) 的不等式符号全部取反,即所有值(不是下标、大 ......
【学习笔记】决策单调性与四边形不等式
Itst - 决策单调性与四边形不等式 学习笔记。 这方面是真的一点不会啊。学点东西吧 apj。 约定 对于 \(n \times m\) 的矩阵 \(A\),定义: 子矩阵 \(A_{[i_1, i_2, \cdots, i_k],[j_1, j_2, \cdots, j_l]}\) 为矩阵 \( ......
计算机图形学中的正交透视——从平行线消失点开始
平行线消失点 在我们日常生活中,会发现这样一类现象:在照片或者图画上,原本是平行的物体(比如铁轨轨道,公路等)会随着他们的延伸逐渐相交于视野尽头,这个尽头就被称作消失点,类似于下面这幅图所显示的内容: 为什么原本平行的物体会出现这样的现象呢?我们可以从几何光学的角度直观的分析一下: 首先我们要大概了 ......
css 背景样式 梯形/平行四边形
绘制这种不规则的背景图形,目前我的思路是使用伪元素 伪元素的优点在于不用添加新的元素 实现平行效果使用了css transform: skew(); 具体代码如下 { position: relative; padding-left: 12px; color: #2187FF; background ......
【matplotlib 实战】--平行坐标系
平行坐标系是一种统计图表,它包含多个垂直平行的坐标轴,每个轴表示一个字段,并用刻度标明范围。通过在每个轴上找到数据点的落点,并将它们连接起来形成折线,可以很容易地展示多维数据。随着数据增多,折线会堆叠,分析者可以从中发现数据的特性和规律,比如发现数据之间的聚类关系。 尽管平行坐标系与折线图表面上看起 ......
诗人小G (恶心的四边形不等式证明)
前言: 没有前言(快累死了,不想写)。 solution: 题目传送门 设$ f_i $ 为第 $ i $ 句时最小的不协调度。 \[f_i = f_j + \left |s_i-s_j+i-j-1-L\right |^P \]\[f_i=f_j+\left |s_i+i-(s_j+j)-(L+1) ......
场强垂直或平行于地面
场强垂直或平行于地面 来源 https://www.zhihu.com/question/276141898 作者 https://www.zhihu.com/people/ailei-da-yang 1. 极化方式的重要性极化是天线一个非常重要的指标。天线的S参数决定信号能不能进入天线,增益决定天 ......
决策单调性与四边形不等式 学习笔记
零、前置知识 子矩阵: 设 \(A\) 为 \(n\times m\) 的矩阵,则子矩阵 \(A_{[i_1,\cdots,i_k],[j_1,\cdots,j_l]}\) 为矩阵 \(A\) 的第 \(i_1,\cdots,i_k\) 行与第 \(j_1,\cdots,j_l\) 列的交形成的矩阵 ......
决策单调性 四边形不等式
# 理论知识 # 整体二分优化递推 注意用词,这里的式子大概是 $f_{i}=g_{j}+w(i,j)$ 的形式,那么如果能满足 $g$ 是预先知道的值且使得 $f_{i_1}$ 和 $f_{i_2}$($i_1<i_2$)取到最优值的点 $j_1j_2$ 满足 $j_1\le j_2$,那么我们称 ......
css 收货地址的平行四边形红蓝白色样式
.line { width: 100%; background: repeating-linear-gradient( -45deg, rgba(0, 41, 136, 0.4) 0px 24px, #fff 24px 48px, rgba(238, 0, 7, 0.4) 48px 72px, #f ......
平行接近法导引弹道仿真
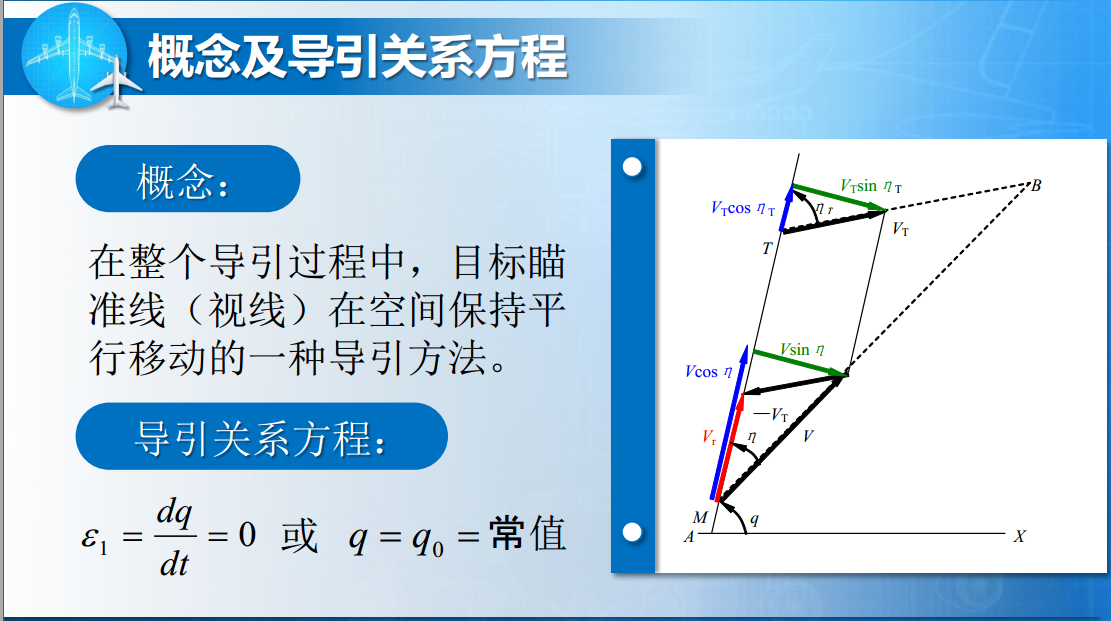 的无监督非平行多对多声音转换(VC)方法,称为StarGAN v2。通过使用对抗性源分类器损失和感知损失的组合,我们的模型明显优于先前的VC模型。虽然我们的模型仅通过20名英语讲话 ......
四边形不等式
写的有点答辩了。 [四边形不等式优化](https://oi-wiki.org/dp/opt/quadrangle/) 最简单的一种: 2D1D的状态转移方程: $$f_{l,r}=\min_{k=l}^{r-1}\{f_{l,k}+f_{k+1,r}\}+w(l,r)$$ 当 $w(l,r)$ 满 ......
四边形不等式小整理
原文:[四边形不等式优化dp](https://www.cnblogs.com/a1b3c7d9/p/10984353.html "四边形不等式优化dp") 以下为内容摘录: 若二元函数满足当 $a \leq b \leq c \leq d$,有 $w(a,d)+w(b,c) \geq w(a,c) ......
纯css 四边形的角样式(只有两个角是三角,其他两个是线段)
效果如图: 核心:使用伪类 代码如下: <div class="box-style"></div> .box-style { position: relative; //纯css只有四个角有边框的样式 box-shadow: 0px 0px 12px 1px #003ba26b inset; bac ......
从决策单调性到四边形不等式
# 从决策单调性到四边形不等式 今天上课浅学了一下,还是有点懵,于是就准备用这篇博文整理一下。 本篇文章主要讨论四边形不等式在有关 1D/1D 类问题中的应用,区间类暂不涉及。 参考:OI-Wiki ## 引入 我们为什么需要决策单调性? 我们之前常见的 dp 优化有很多,如单调队列,如斜率优化,如 ......
泊车路径拟合 平行泊车 垂直泊车 多项式函数 反正切函数
泊车路径拟合 平行泊车 垂直泊车 多项式函数 反正切函数 正弦函数 余弦函数 路径拟合根据已知的平行泊车 垂直泊车离散点信息 利用相关的函数进行再拟合 并进行泊车动示意 (可根据自身需求更换路径信息)所有资料均包括:1、相关问题的文档分析2、matlab 代码及相关注释3、为脚本文件对版本无硬性要求 ......
平行泊车、垂直泊车matlab程序仿真,效果不错,实现泊车路线规划。
平行泊车、垂直泊车matlab程序仿真,效果不错,实现泊车路线规划。含部分参考说明ID:88150632200073070 ......
Three.js教程:平行光与环境光
推荐:将NSDT场景编辑器加入你的3D工具链 其他系列工具:NSDT简石数字孪生 平行光与环境光 本节课通过平行光DirectionalLight (opens new window)和环境光AmbientLight (opens new window)进一步了解光照对应模型Mesh表面的影响。 点 ......
APIO2021《决策单调性与四边形不等式》讲稿与相关材料
两年多过去了,今天还有人加我来问 APIO21 我的四边形不等式讲稿,我一感到受宠若惊,另外对没有及时公开相关材料感到很抱歉。目前所有材料已上传到 [github](https://github.com/Itst00/APIO2021-monge/tree/main)。 ......
四边形不等式优化dp
对于转移方程 $c(i,j)=w(i,j)+\min_d(c(i,d)+c(d+1,j))$,存在 $w(i,j)+w(i',j')\le w(i,j')+w(i',j)(i\le i'\le j\le j'$ 如何快速求其答案。 引理一:$w(i,j)+w(i',j')\le w(i,j')+w( ......
winform C# 平行替代产品
1、Lazarus IDE 编译后的exe文件很大。 安装方便,安装文件200Mb 2、aardio 入手,debug有点困难 有些库需要联网,不纯离线开发 3、PyQt5 没研究,估计也是要联网,不是纯离线开发 ......